压力仅作用在砌体部分面积上的受力状态称为局部受压,如图5.44所示。局部受压是砌体结构中常见的受力形式。砌体局部受压强度不足可能导致砌体墙、柱破坏,危及整个结构的安全。

图5.44 局部受压示意
1.局部受压类型
按压力分布情况不同可分为两种情况:当砌体截面上作用局部均匀压力时,称为局部均匀受压;当砌体截面上作用局部非均匀压力时,则称为局部不均匀受压。砌体局部受压有多种形式。按局压面积Al与其受压底面积A0的相对位置不同,局部受压可分为中心局压、墙边缘局压、墙中部局压、墙端部局压及墙角部局压等,如图5.44(a)所示。按局压应力的分布情况,可分为均匀局压及不均匀局压,如图5.44(b)所示,前者如钢筋混凝土柱或砖柱支承于砌体基础上,后者如钢筋混凝土梁支承于砖墙上的情况。
这些情况的共同特点是砌体支承着比自身强度高的上层构件,上层构件的总压力通过局部受压面积传递给本层砌体构件。在这种受力状态下,不利的一面是在较小的承压面积上承受着较大的压力,有利的一面是砌体局部受压强度高于其抗压强度。其原因是在轴向压力作用下,由于力的扩散作用,如图5.45(a)所示,不仅直接承压面下的砌体发生变形,而且在它的四周也发生变形,离直接承压面愈远变形愈小。这样,由于砌体局部受压时未直接受压的四周砌体对直接受压的内部砌体的横向变形具有约束作用,即“套箍强化”作用,产生了三向或双向受压应力状态,如图5.45(b)所示,因而其局部抗压强度比一般情况下的抗压强度有较大的提高。当砌体局压强度不足时,可在梁、柱下设置钢筋混凝土垫块,以扩大局压面积Al。垫块的形式有整浇刚性垫块、预制刚性垫块、柔性垫梁及调整局压力作用点位置的特殊垫块。
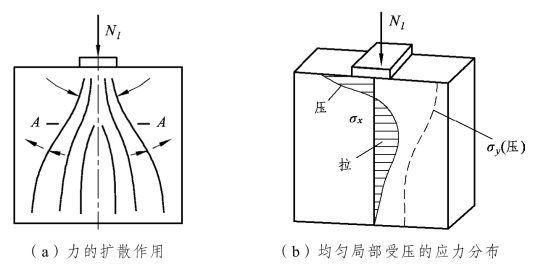
图5.45 局部受压力的扩散和应力分布
2.局部均匀受压
局部均匀受压是局部受压的基本情况,在工程中并不多见,但它是研究其他局部受压类型的基础。根据大量的局部受压试验,可知局部受压强度的提高主要取决于砌体原有的轴心抗压强度和周围砌体对局部受压区的约束程度。局部均匀受压,随着A0/Al比值的不同,可能有竖向裂缝发展而破坏、劈裂破坏和局部压碎三种破坏形态,如图5.46所示。
竖向裂缝发展而破坏:初裂往往发生在与垫块直接接触的l~2皮砖以下的砌体,随着荷载的增加,纵向裂缝向上、向下发展,同时也产生新的竖向裂缝和斜向裂缝,如图5.46(a)所示,一般来说它在破坏时有一条主要的竖向裂缝。在局部受压中,这是较常见也是最基本的破坏形态。

图5.46 局压破坏形态
劈裂破坏:这种破坏形态的特点是,在荷载作用下,纵向裂缝少而集中,一旦出现纵向裂缝,砌体即犹如刀劈而破坏,如图5.46(b)所示。试验表明,只有当局部受压面积与砌体面积之比相当小,才有可能产生这种破坏形态。砌体局压破坏时初裂荷载与破坏荷载十分接近。这种破坏为突然发生的脆性破坏,危害极大,在设计中应避免出现这种破坏。
局部压碎:这种情况较少见,一般当墙梁的墙高与跨度之比较大,砌体强度较低时,有可能产生梁支承附近砌体被压碎的现象,如图5.46(c)所示。
1)局部均匀受压承载力验算
砌体截面中受局部均匀压力时的承载力,应满足下式的要求:
![]()
式中 Nl——局部受压面积上的轴向力设计值(N);
γ——砌体局部抗压强度提高系数;
f——砌体的抗压强度设计值(MPa),局部受压面积小于0.3m2,可不考虑强度调整系数γa的影响;
Al——局部受压面积(mm2)。
2)砌体局部抗压强度提高系数
砌体局部抗压强度提高系数γ,可按下式计算:

式中 A0——影响砌体局部抗压强度的计算面积。
计算所得的γ值,尚应符合下列规定:
(1)在图5.47(a)“中心”局部受压的情况下,γ≤2.5。
(2)在图5.47(b)一般墙段“中部边缘”局部受压的情况下,γ≤2.0。
(3)在图5.47(c)墙“角部”局部受压的情况下,γ≤1.5。
(4)在图5.47(d)墙“端部”局部受压的情况下,γ≤1.25。
(5)按《砌体结构设计规范》要求灌孔的混凝土砌块墙体,在(1)(2)的情况下,尚应符合γ≤1.5;未灌孔混凝土砌块砌体,γ=1.0。
(6)对多孔砖砌体孔洞难以灌实时,应按γ=1.0取用;当设置混凝土垫块时,按垫块下的砌体局部受压计算。
3)影响砌体局部抗压强度的计算面积A
可按下列规定采用:
(1)在图5.47(a)的情况下 A0=(a+d+h)h
(2)在图5.47(b)的情况下 A0=(b+2h)h
(3)在图5.47(c)的情况下 A0=(a+h)h+(b+h1-h)h1
(4)在图5.47(d)的情况下 A0=(a+h)h
式中 a,b——矩形局部受压面积Al的边长;
h,h1——墙厚或柱的较小边长;
d——矩形局部受压面积的外边缘至构件边缘的较小距离,当大于h时,应取为h。

图5.47 影响局部抗压强度的面积
3.梁端支承处砌体的局部受压
钢筋混凝土梁或屋架支承在砖墙上时,梁或屋架与砖墙的接触面只是墙体截面的一部分,这就是典型的梁端支承处砌体局部受压。梁端支承处砌体的局部受压面积上除了承受梁端传来的支撑压力Nl外,还承受由上部荷载产生的轴向力N0。
1)局部受压承载力计算公式
梁端支承处砌体的局部受压承载力应按下列公式计算:

式中 ψ——上部荷载的折减系数,当A0/Al≥3时,应取ψ等于0;
N0——局部受压面积内上部轴向力设计值(N);
Nl——梁端支承压力设计值(N);
σ0——上部平均压应力设计值(N/mm2);
η——梁端底面压应力图形的完整系数,应取0.7,对于过梁和墙梁取1.0;
a0——梁端有效支承长度(mm),当a0大于a时,应取a0等于a,a为梁端实际支承长度(mm);
b——梁的截面宽度(mm);
hc——梁的截面高度(mm);
f——砌体的抗压强度设计值(MPa)。
2)梁的有效支承长度
当梁直接支承在砌体上时,由于梁的弯曲和支承处砌体压缩变形的影响,梁端与砌体接触的长度并不等于实际支承长度a,而为有效支承长度a0, a0≤a,如图5.48所示。此时砌体局部受压面积Al=a0b。梁端有效支承长度a0与Nl大小、支承情况、梁的刚度及梁端底面砌体的弹塑性有关。

图5.48 梁的有效支承长度
经试验分析,为了便于工程应用,《砌体结构设计规范》给出梁的有效支承长度的计算公式,即式(5.47)。
3)上部荷载对砌体局部抗压强度的影响
一般梁端支承处局部受压的砌体,除承受梁端支承压力Nl外,还可能有上部荷载产生的轴向力N0,如图5.49所示。
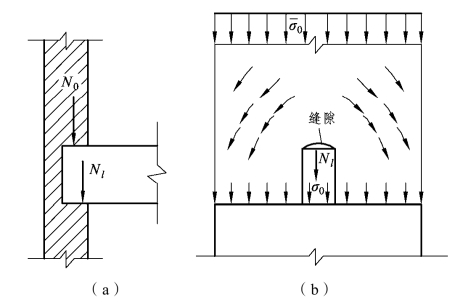
图5.49 上部荷载对局部抗压强度的影响
试验表明,当N0较小、Nl较大时,梁端底部的砌体将产生压缩变形,使梁端顶部与砌体接触面减少,甚至脱开,产生水平缝隙。原来由上部砌体传给梁端支承面上的压力N0将转而通过上部砌体自身的内拱作用传给梁端周围的砌体。上部荷载σ0的扩散对梁端下局部受压的砌体起了横向约束作用,对砌体的局部受压是有利的。上部荷载σ0对梁端下局部受压砌体的影响主要与A0/Al比值有关。当A0/Al足够大时,内拱卸荷作用就可形成。《砌体结构设计规范》采用上部荷载折减系数ψ来反映这种有利因素的影响。
4.梁端刚性垫块下砌体局部受压
1)刚性垫块下的砌体局部受压承载力
刚性垫块下的砌体局部受压承载力,应按下列公式计算:

式中 N0——垫块面积Ab内上部轴向力设计值(N);
σ0——上部平均压应力设计值(N/mm2);
γ1——垫块外砌体面积的有利影响系数,γ1应为0.8γ,但不小于1.0,γ为砌体局部抗压强度提高系数,按式(5.42)以Ab代替Al计算得出;
Ab——垫块面积(mm2);
ab——垫块伸入墙内的长度(mm);
bb——垫块的宽度(mm);
φ——垫块上N0及Nl合力的影响系数,采用表5.18~5.20中β≤3时的φ值,e 为N0、Nl合力对垫块形心的偏心距,Nl距垫块边缘的距离可取0.4a0,e 按下式计算:

式中 a0——设刚性垫块时的梁端有效支承长度(mm)。
2)梁端有效支承长度
设刚性垫块时,梁端有效支承长度a0应按下式确定:

式中 δ1——刚性垫块的影响系数,可按表5.23采用。
表5.23 系数δ1

试验和有限元分析表明,垫块上表面a0较小,这对于垫块下局部受压承载力计算影响不是很大(有垫块时局部压应力大为减小),但可能对其下的墙体受力不利,增大了荷载偏心距,因此有必要给出垫块上表面梁端有效支承长度,可采用式(5.52)计算。对于采用与梁端现浇成整体的刚性垫块与预制刚性垫块下局部受压有些区别,但为简化计算,也可按后者计算。(https://www.xing528.com)
3)刚性垫块的构造要求
刚性垫块的构造,应符合下列规定:
(1)刚性垫块的高度不宜小于180mm,自梁边算起的垫块挑出长度不宜大于垫块高度tb。
(2)在带壁柱墙的壁柱内设刚性垫块时,其计算面积应取壁柱范围内的面积,而不应计算翼缘部分,同时壁柱上垫块伸入翼墙内的长度不应小于120mm。
(3)当现浇垫块与梁端整体浇筑时,垫块可在梁高范围内设置。

图5.50 梁端下预制刚性垫块
5.梁端垫梁下砌体局部受压
在实际工程中,常在梁或屋架端部下面的砌体墙上设置连续的钢筋混凝土梁,如圈梁等。此钢筋混凝土梁可把承受的局部集中荷载扩散到一定范围的砌体墙上,起到垫块的作用,故称为垫梁,如图5.51所示。柔性垫梁可视为弹性地基上的无限长梁,墙体即为弹性地基。如将局压破坏荷载Nl作用下按弹性地基梁理论计算出砌体中最大压应力σmax与砌体抗压强度fm的比值记作γ,则试验发现γ 均在1.6以上。这是因为柔性垫梁能将集中荷载传布于砌体的较大范围。应力分布可近似视为三角形,其长度l=πh0。h0为垫梁的折算高度。根据力的平衡条件可写出:

则有


图5.51 垫梁局部受压
根据试验结果,考虑垫梁上可能存在的上部荷载作用,取γ=1.5,则可写出下式:
![]()
将式(5.54)代入得

上式中还应考虑Nl沿墙厚方向产生不均匀分布压应力的影响,为此引入垫梁底面压应力分布系数δ2。综上所述,钢筋混凝土垫梁受上部荷载N0和集中局部荷载Nl作用,且垫梁长度大于πh0时,垫梁下的砌体局部受压承载力按下列公式计算:

式中 Nl——垫梁上集中局部荷载设计值(N);
N0——垫梁在πbbh0/2范围内由上部荷载设计值产生的轴向力(N);
bb——垫梁宽度(mm);
δ2——当荷载沿墙厚方向均匀分布时 δ2取1.0,不均匀时δ2可取0.8;
f——砌体的抗压强度设计值(MPa);
h0——垫梁折算高度(mm);
Eb,Ib——垫梁的混凝土弹性模量(N/mm2)和截面惯性矩(mm4);
E——砌体的弹性模量(N/mm2);
h——墙厚(mm)。
【例5.7】 验算房屋外纵墙上跨度为5.8m的大梁端部下砌体局部受压的承载(图5.52)。已知大梁截面尺寸为200mm×550mm,实际支承长度a=240mm,支座反力Nl=80kN,梁底墙体截面处的上部设计荷载值为240kN,窗间墙截面1 200mm×390mm,采用孔洞率不大于35%的双排孔轻集料混凝土小型空心砌块,等级为MU10,以及Mb5等级的砂浆砌筑。试验算梁端砌体的局部受压承载力。

图5.52 例5.7图
【解】 (1)求f值。
查表5.11得抗压强度设计值为2.45MPa;因系双排组砌的轻集料混凝土砌块砌体,应乘以折减系数0.8,则f=0.8×2.45=1.96(MPa)。
(2)求A0,Al。

梁端有效支承长度取a0=167.5mm计算,则:

(3)求γ值。
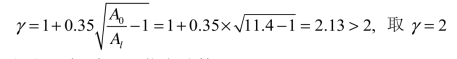
(4)局部受压承载力验算。
应力图形的完整性系数η=0.7,则:
ηγfAl=0.7×2×1.96×0.033 5=92(kN)>ψN0+Nl=80(kN)
梁端砌体的局部受压安全。
【例5.8】 房屋外纵墙上跨度为5.8m的大梁端部下砌体局部受压(图5.53),已知大梁截面尺寸为200mm×550mm,实际支承长度a=240mm,支座反力Nl=110kN并采用刚性垫块,预制刚性垫块尺寸为ab×bb×tb=240mm×600mm×200mm,梁底墙体截面处的上部设计荷载值为240kN,窗间墙截面1 100mm×390mm,采用孔洞率不大于35%的双排孔轻集料混凝土小型空心砌块,等级为MU10及Mb5等级的砂浆砌筑。试验算局部受压承载力。
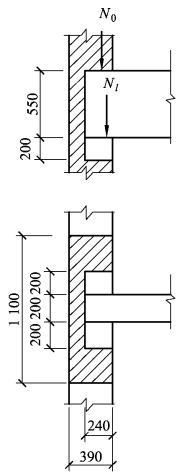
图5.53 例5.8图
【解】 (1)求f值。
查表5.11得抗压强度设计值为2.45MPa;因系双排组砌的轻集料混凝土砌块砌体,应乘以折减系数0.8,则f=0.8×2.45=1.96MPa。
(2)求A0,Ab。
tb=200mm>180mm(满足刚性垫块要求)
bb-b=600-200=400(mm)=2tb
bb+2h=600+2×390=1 380(mm)>1 100(mm)(窗间墙长),取bb+2h=1 100mm,A0=(bb+2h)h=1 100×390=429 000(mm2)。
Ab=ab×b=240×600=144 000(mm2)
(3)求γ1值。

(4)求N0值。

作用在垫块上的
N0=σ0Ab=0.56×144 000(N)=80.64(kN)
(5)求φ值(据β≤3及e/h查表)。
σ0/f=0.56/1.96=0.29,查表得δ1=5.84
梁端有效支承长度:
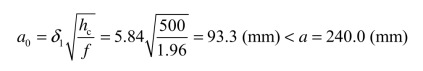
取a0=93.3mm,Nl作用点离边缘为0.4a0=0.4×93.3=37.3(mm),对垫块形心的偏心距e为

(6)局部受压承载力验算。
φγ1fAb=0.68×1.20×1.96×0.144×103=230(kN)>N0+Nl=190.64(kN)
局部受压承载力满足要求。
【例5.9】 某窗间墙截面1 100mm×390mm(图5.54),采用孔洞率不大于35%的双排孔轻料混凝土小型空心砌块,等级为MU10以及Mb5等级的砂浆砌筑。房屋外纵墙上跨度为5.8m的大梁端部下采用垫梁,已知大梁截面尺寸为b×h=200mm×500mm,实际支承长度a=240mm,支座反力Nl=110kN,垫梁尺寸为bb×hb=240mm×180mm,采用C20级混凝土浇筑,梁底墙体截面处的上部设计荷载值为240kN。验算垫梁下的砌体局部受压承载力。
【解】 (1)求f值。
查表5.11得抗压强度设计值为2.45MPa;因系双排组砌的轻集料混凝土砌块砌体,应乘以折减系数0.8,则f=0.8×2.45=1.96MPa。
E=1 500f=1 500×1.96(MPa)=2 940(MPa)

图5.54 例5.9图
(2)求h0。

由《混凝土结构设计规范》(GB 50010—2010)表4.1.5查得Ec=2.55×104MPa。

(3)求δ2值。
荷载沿墙厚不均匀分布,所以δ2取0.8。
(4)求N0值。

(5)局部受压承载力验算。
2.4δ2fbhh0=2.4×0.8×1.96×240×274.8=248.19(kN)
N0+Nl=57.99+110=167.99(kN)<2.4δ2fbhh0=248.19(kN)
局部受压承载力满足要求。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




