受压构件承载力计算方法

1.单向偏心受压构件

1）单向偏心受压构件试验

（1）受压短柱（β≤3，e≠0）

当受压构件的计算高度H0与截面计算方向边长h 之比，即高厚比β不大于3时，称为短柱，此时可不考虑构件纵向弯曲对承载力的影响。试验表明，短柱在轴向力作用下当偏心距不同时，其截面上的应力分布状态是变化的（图5.38）。

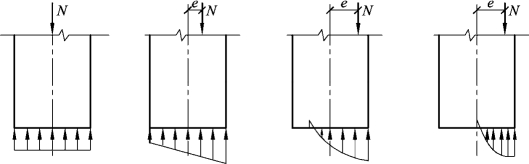
图5.38　砌体受压的截面应力变化

砌体短柱在轴心荷载作用下，砌体内横截面在各阶段的应力都是均匀分布的。而构件在偏心荷载作用下的受力特性将发生很大变化。当偏心距不大时，整个截面受压，由于砌体的弹塑性性能，截面中的应力呈曲线分布，靠近轴向力一侧压应力较大，远离轴向力一侧压应力较小。随着偏心距的不断增大，远离轴向力一侧截面边缘的应力逐步由受压过渡到受拉，但只要受拉边的拉应力尚未达到砌体沿通缝的抗拉强度，受拉边就不会出现开裂；当偏心距进一步增大，一旦截面受拉边的拉应力超过砌体沿通缝的抗拉强度时，受拉边将出现沿通缝截面的水平裂缝，这种情况属于正常使用极限状态，已开裂处的截面退出工作。在这种情况下，裂缝在开裂后和破坏前都不会无限制地增大而使构件发生受拉破坏，而是在剩余截面和已经减少了偏心距的荷载作用下达到新的平衡。这种平衡随裂缝的不断展开被打破，进而又达到一个新的平衡。剩余截面的压应力进一步加大，并出现竖向裂缝。最后由于受压承载能力耗尽而破坏。破坏时，虽然砌体受压一侧的极限变形和极限强度都比轴压构件高，但由于压应力不均匀的加剧和受压面的减少，截面所能承担的轴向压力将随偏心距的增大而明显下降。必须指出，由于砌体具有弹塑性性能，且具有局部受压性质，故在破坏时，砌体受压一侧的极限变形和极限强度均比轴压高，提高的程度随偏心距的增大而加大。

（2）轴心受压长柱（β＞3，e=0）

细长柱和高而薄的墙，在轴心受压时，由于偶然偏心的影响，往往会产生侧向变形，并导致构件发生纵向弯曲从而降低其承载力。偶然偏心包括轴向力作用点与截面形心不完全对中（几何偏心），以及由于构件材料性质不均匀而导致的轴力作用点与截面形心的不对中（物理偏心）。长柱的承载力将比短柱有所下降，下降的幅度与砂浆的强度等级及构件的高厚比有关。

对于砌体构件，由于大量灰缝的存在以及块体和灰缝的匀质性较差，增加了偶然偏心的概率；砂浆的变形模量还随应力的增高而大幅度降低，这些都会导致砌体构件中纵向弯曲的不利影响比混凝土构件更为严重。试验表明，对于砌体构件，当其高厚比β＞3时，应考虑纵向弯曲的影响。

（3）偏心受压长柱（β＞3，e≠0）

细长柱在偏心压力作用下，会由于纵向弯曲的影响在原有偏心距e 的基础上产生附加偏心距ei，使荷载偏心距增大，而附加弯矩的存在又加大了柱的侧向变形，如此交互作用加剧了长柱的破坏（图5.39）。随着偏心压力的增大，柱中部截面水平裂缝逐步开展，同时受压面积缩小，压应力增大；当压应力达到抗压强度时，柱即破坏。

为了准确地估计偏压长柱的承载能力，应当考虑砌体的材料非线性和几何非线性，进行全过程分析。但这种分析相当复杂，不便实用。因此，当前各国规范多采用基于试验的简化计算方法。我国砌体结构设计规范采用附加偏心距法进行偏压长柱的承载力计算。

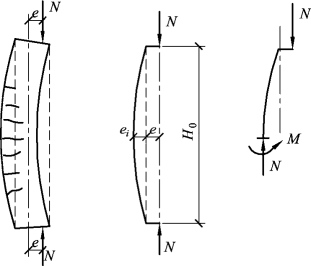
图5.39　偏压长柱的受力分析

2）受压构件承载力计算

砌体的抗拉、抗弯和抗剪强度远低于其抗压强度，所以无筋砌体主要用作受压构件。对于无筋砌体受压构件，无论是轴心受压或偏心受压，长柱或短柱，都采用下式的承载力设计计算公式：

式中　N——轴向压力设计值（N）；

　　　f——砌体抗压强度设计值（MPa），见表5.7～5.13；

　　　A——截面面积（对各类砌体均按毛面积计算）（mm2），带壁柱墙的计算截面翼缘宽度，可按下列规定采用：①多层房屋，当有门窗洞口时，可取窗间墙宽度；当无门窗洞口时，每侧翼墙宽度可取壁柱高度（层高）的1/3，但不应大于相邻壁柱间的距离；②单层房屋，可取壁柱宽加2/3墙高，但不应大于窗间墙宽度和相邻壁柱间的距离；③计算带壁柱墙的条形基础时，可取相邻壁柱间的距离；

　　　φ——高厚比β和轴向力偏心距e对受压构件承载力的影响系数。

对矩形截面构件，当轴向力偏心方向的截面边长大于另一方向的边长时，除按偏心受压计算外，还应对较小边长方向按轴心受压进行验算。

（1）受压构件的承载力影响系数

受压构件承载力影响系数φ是高厚比β和轴向力偏心距e 对受压构件承载力的影响系数，按照附加偏心距的分析方法并结合试验研究结果，计算公式如下：

式中　e——荷载设计值产生的偏心距，e=M/N（M、N分别为作用在受压构件上的弯矩、轴向力设计值），按内力设计值计算的轴向力的偏心距e不应超过0.6y（y为截面重心到轴向力所在偏心方向截面边缘的距离），如图5.40所示；

　　　h——矩形截面荷载偏心方向的边长，计算T形截面时，应以折算厚度hT=3.5i（i为T形截面的回转半径）代替截面在偏心方向上的高度h；

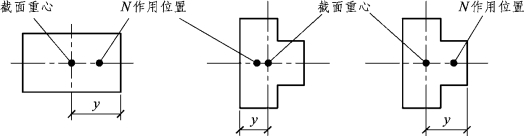
图5.40　偏心距e限值

　　　φ0——轴心受压构件的稳定系数，按下式计算：

其中　β——构件高厚比，当β≤3时，取φ0=1；

　　　α——与砂浆强度等级有关的系数：当砂浆强度等级大于或等于M5时取0.001 5；当砂浆强度等级等于M2.5时取0.002；当砂浆强度为0时取0.009。

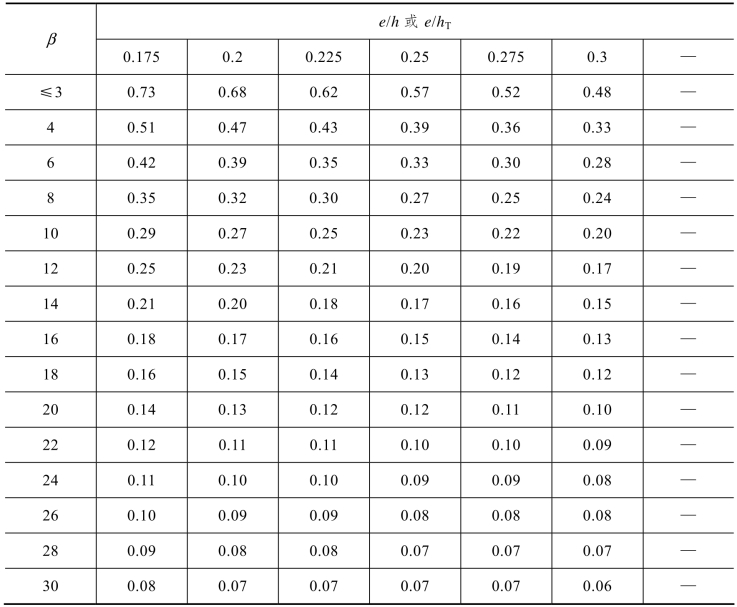
无筋砌体矩形截面单向偏心受压构件承载力影响系数，可按式（5.34）计算，也可表按5.18～表5.20查用。

表5.18　影响系数φ（砂浆强度等级≥M5）

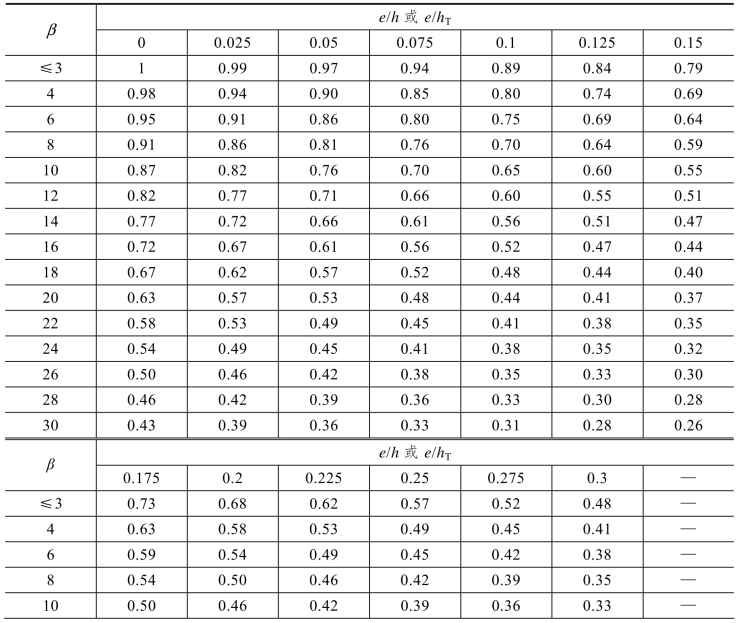
续表

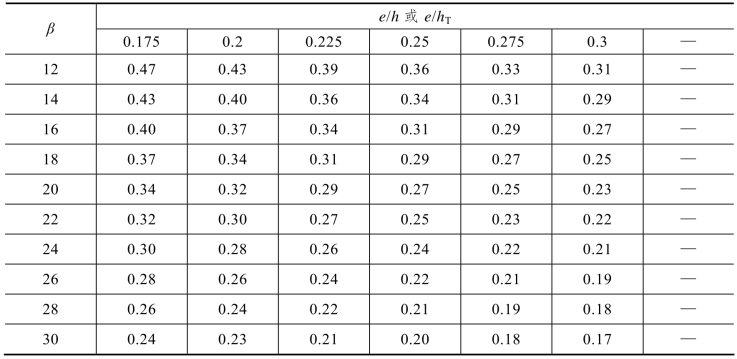
表5.19　影响系数φ（砂浆强度等级M2.5）

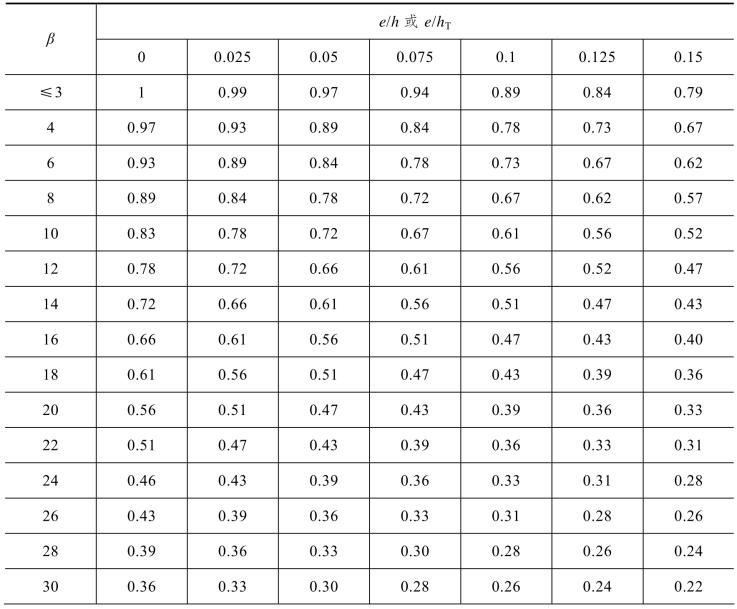
续表

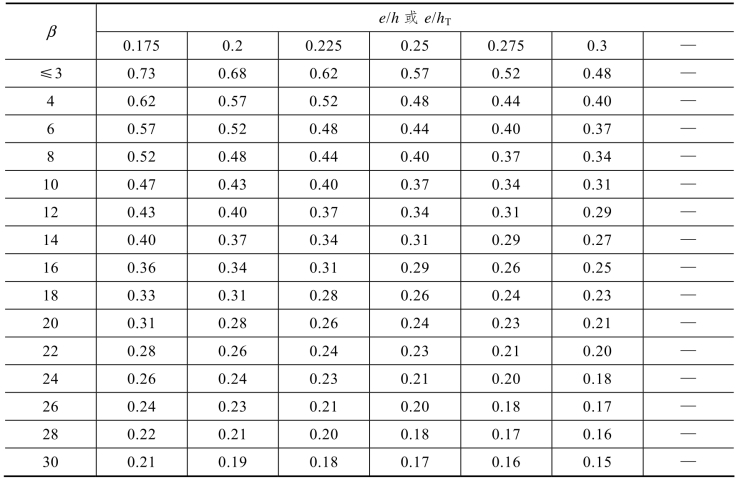
表5.20　影响系数φ（砂浆强度0）

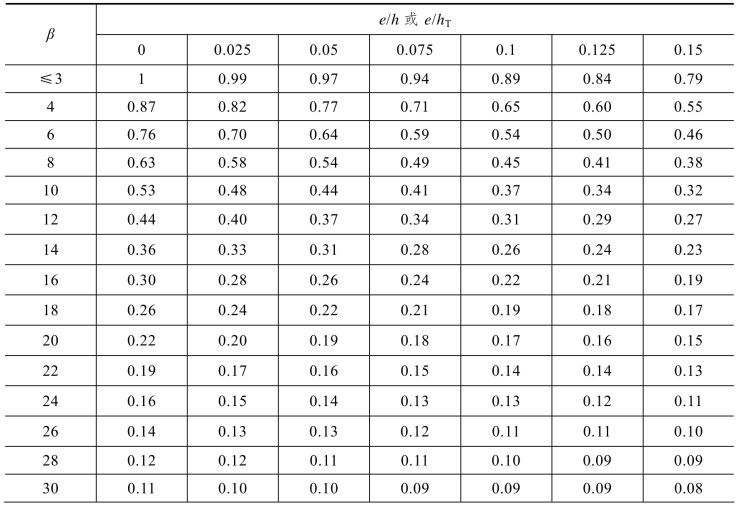
续表

（2）高厚比及调整

确定影响系数φ 时，考虑不同类型砌体受压性能的差异，构件的高厚比β应乘以调整系数γβ。构件高厚比β是指构件的计算高度H0与截面在偏心方向上的高度h的比值。

①矩形截面

②T形截面

式中　γβ——不同材料砌体构件的高厚比修正系数，按表5.21采用；

　　　H0——受压构件的计算高度，按表5.22确定；

　　　h——矩形截面轴向力偏心方向的边长，当轴心受压时为截面较小边长；

　　　hT——T形截面的折算厚度，可近似按3.5i计算，其中i为截面回转半径。

表5.21　高厚比修正系数γβ

（3）受压构件的计算高度

受压构件的计算高度H0，应根据房屋类别和构件支承条件等按表5.22采用。表中的构件高度H0应按下列规定采用。

①在房屋底层，H0为楼板顶面到构件下端支点的距离。下端支点的位置，可取在基础顶面。当埋置较深且有刚性地坪时，可取室外地面以下500mm处。

②在房屋其他层，H0为楼板或其他水平支点间的距离。

③对于无壁柱的山墙，可取层高加山墙尖高度的1/2；对于带壁柱的山墙可取壁柱处的山墙高度。

对于变截面柱，如无吊车，或者虽有吊车但不考虑吊车作用时，变截面柱上段的计算高度可按表5.22规定采用。变截面柱下段的计算高度可按下列规定采用：

①当Hu/H≤1/3时，取无吊车房屋的H0。

②当1/3＜Hu/H＜1/2时，取无吊车房屋的H0乘以修正系数μ：μ=1.3-0.3Iu/IL（Iu为变截面柱上段的惯性矩；IL为下段的惯性矩）。

③当Hu/H≥1/2时，取无吊车房屋的H0，但在确定β值时，应采用上柱的截面。

表5.22　受压构件的计算高度H0

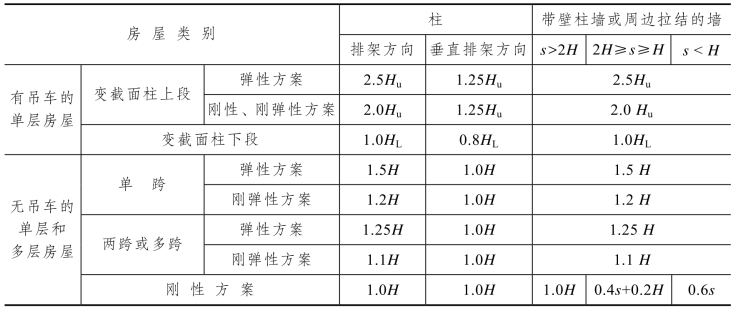
注：①表中Hu为变截面柱的上段高度，s为周边拉结墙的水平距离，HL为变截面柱的下段高度；②对于上端为自由端的构件，H0=2H；③独立砖柱，当纵向柱列无柱间支撑或柱间墙时，柱在垂直排架方向的H0，应按表中数值乘以1.25后采用；④自承重墙的计算高度应根据周边支承或拉结条件确定。

【例5.1】　截面为490mm×600mm的砖柱，采用强度等级为MU15的蒸压粉煤灰普通砖和M5混合砂浆砌筑，柱的计算长度H0=6m，轴向压力设计值N=380kN，试验算该柱的承载力是否满足安全性要求。

【解】　（1）求A值。

A=0.49×0.60=0.294(m2)＜0.3(m2)，强度调整系数γa=0.7+0.294=0.994。

（2）求f值。

査表5.9得砌体抗压强度设计值为1.83MPa。

f=1.83γa=1.83×0.994(MPa)=1.819(MPa)

（3）求φ值。

査表5.21高厚比修正系数γβ=1.2。

（4）承载力验算。

φAf=(0.755×0.294)×(1.819×103)=403.8(kN)＞380(kN)

该柱的承载力满足安全性要求。

【例5.2】　截面为490mm×370mm的砖柱，采用MU10烧结普通砖和M5混合砂浆砌筑。柱的计算高度3.2m（两端为不动铰接），柱顶承受轴向力标准值Nk=160kN，其中永久荷载产生的轴向力标准值为130kN，可变荷载产生的轴向力标准值为130kN，可变荷载组合值系数为0.7，试验算该柱的承载力是否满足安全性要求。

【解】　（1）求A值。

A=0.49×0.37=0.18(m2)＜0.3(m2)

强度调整系数γa=0.7+A=0.7+0.18=0.88

（2）求f值。

査表5.7得砌体抗压强度设计值为1.50MPa。

f=1.50γa=1.50×0.88(MPa)=1.32(MPa)

（3）求φ值。

査表5.21高厚比修正系数γβ=1.0。

（4）求柱底轴向力设计值。

永久荷载起控制作用时：

N=γGGk+γQQk=1.35×(130+0.49×0.37×3.2×19)+1.4×0.7×30=219.8(kN)

可变荷载起控制作用时：(www.xing528.com)

N=γGGk+γQQk=1.2×(130+0.49×0.37×3.2×19)+1.4×30=211.2(kN)

因此，N＝219.8kN。

（5）承载力验算。

柱底截面的抗力设计值：

Nu=φfA=0.9×1.32×490×370=215.4(kN)＜N=219.8(kN)

该柱的承载力不满足安全性要求。

【例5.3】　某一刚性方案的多层房屋中，有一厚190mm的轴心受压内横墙（墙体面积大于0.3m2），采用MU5单排孔且对孔砌筑的小型混凝土空心砌块（390mm×190mm×190mm）和Mb5砂浆砌筑；双面石灰粗砂粉刷墙已知作用在底层墙底的外荷载产生的轴力设计值为118kN/m，墙底自重产生的轴力设计值为13.80kN/m，纵墙间距6.8m，横墙间距3.4m，H＝3.5m。试验算该墙的承载力是否满足安全性要求。

【解】　（1）求A值。

墙体面积大于0.3m2，取1m墙长为计算单元、厚190mm的承重内横墙截面面积A＝1m/m×0.19m＝0.19m2/m。

（2）求f值。

查表5.10得砌体抗压强度设计值取f=1.19MPa。

（3）求φ值。

査表5.21高厚比修正系数γβ=1.1。

查表5.22，H＜纵墙间距s＝6.8m＜2H（若计算横墙荷载时s则为房屋纵墙间距）

（4）求底部截面上轴力。底层墙下部截面轴力设计值为：

N=118+13.80=131.8(kN/m)

（5）承载力验算。

φAf=(0.630×0.19)×(1.19×103)=142.4(kN/m)＞131.8(kN/m)

该墙的承载力满足安全性要求。

【例5.4】　截面为400mm×600mm的单排孔且对孔砌筑小型轻集料混凝土空心砌块独立柱，采用MU15砌块及Mb7.5砂浆砌筑，设在截面两个方向的柱计算高度相同，即H0=5.2m，该柱承受的荷载设计值N＝280kN，在长边方向的偏心距e＝100mm。试验算该柱的承载力是否满足安全性要求。

【解】　（1）偏心方向受压承载力验算（长边方向）。

①求A值。

A=0.4×0.6=0.24(m2)＜0.3(m2)，强度调整系数γa=0.7+0.24=0.94。

②求f值。

査表5.10得砌体抗压强度设计值为3.61MPa，因为是独立柱，还应乘以系数0.7，则f=0.7×0.94×3.61(MPa)=2.38(MPa)。

③求φ值。

査表5.21高厚比修正系数γβ=1.1。

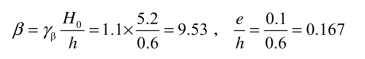
查表5.18或根据式（5.34）计算，得φ=0.527。

④承载力验算。

φAf=(0.527×0.24)×(2.38×103)=301(kN)＞280(kN)

长边方向承载力满足安全性要求。

（2）短边方向按轴心受压验算。

①求φ值。

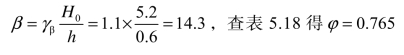
②承载力验算。

φAf=(0.765×0.24)×(2.38×103)=437(kN)＞280(kN)

短边方向承载力满足安全性要求。

【例5.5】　试验算单层单跨无吊车工业厂房窗间墙截面的承载力。房屋柱距为4m，窗间墙截面如图5.41。计算高度H0=6.48m，墙用MU10烧结普通砖及M2.5水泥砂浆砌筑。荷载设计值产生的轴向力N为320kN，荷载设计值产生的偏心距e为0.128m，荷载偏向翼缘侧。试验算该墙的承载力是否满足安全性要求。

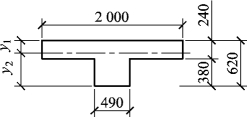
图5.41　墙体截面

【解】　（1）求解截面几何特征。

①面　积：

A=2×0.24+0.49×0.38=0.666 2(m2)＞0.3(m2)

②截面重心位置：

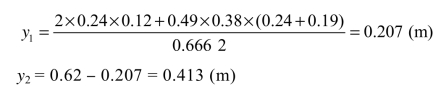
③惯性矩：

④回转半径：

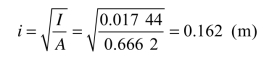
⑤截面折算厚度：

hT=3.5i=3.5×0.162=0.566(m)

（2）求f值。

査表5.7得砌体抗压强度设计值为1.30N/mm2，采用M2.5水泥砂浆，考虑强度调整系数0.9，则f=0.9×1.3(MPa)=1.17(MPa)。

（3）求φ值。

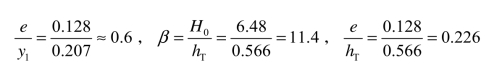
查表5.18或根据式（5.34）计算，φ=0.374。

（4）承载力验算。

Nu=φ f A=0.374×1.17×103×0.666 2=291.5(kN)＜320(kN)

该墙的承载力不满足安全性要求。

2.双向偏心受压构件

轴向压力在矩形截面的两个主轴方向都有偏心距，或同时承受轴心压力及两个方向弯矩的构件，即为双向偏心受压构件，如图5.42所示。

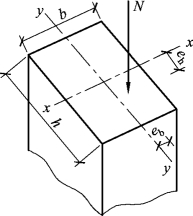
图5.42　双向偏心受压构件

双向偏心受压构件截面承载力的计算，显然比单向偏心受压构件复杂得多。国内外有关研究较少，目前尚无精确的理论求解方法。根据湖南大学的试验研究，《砌体结构设计规范》建议采用附加偏心距法。

矩形截面双向偏心受压构件截面承载力的计算公式：

式中　N——纵向压力设计值；

　　　A——构件截面面积；

　　　f——砌体抗压强度设计值；

　　　φ——承载力影响系数，计算公式如下：

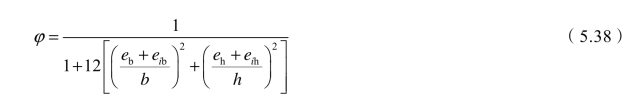
式中　eb，eh——轴向力在截面重心x轴、y轴方向的偏心距（图5.42）；

　　　eib，eih——轴向力在截面重心x轴、y轴方向的附加偏心距，按以下公式计算：

式中　φ0——构件的稳定系数，按式（5.35）计算。

试验表明，当偏心距eb＞0.3b和eh＞0.3h时，随着荷载的增加，砌体内水平裂缝和竖向裂缝几乎同时发生，甚至水平裂缝早于竖向裂缝出现。因而设计双向偏心受压构件时，规定偏心距限值为eb、eh宜分别不大于0.25b和0.25h。附加偏心距法分析还表明，当一个方向的偏心率不大于另一方向偏心率的5%时，可简化按另一方向的单向偏心受压计算，其承载力的计算误差小于5%。

为了简化计算，《砌体结构设计规范》规定，当一个方向的偏心率不大于另一方向的偏心率5%时，可简化按另一个方向的单向偏心受压计算。

上述计算方法与单向偏心受压承载力计算相衔接，且与试验研究结果符合良好。

【例5.6】　双向偏心受压柱，截面尺寸为490mm×620mm（图5.43）。用MU10烧结普通砖和M7.5混合砂浆砌筑。柱的计算高度为4.8m，作用于柱上的轴向力设计值为200kN，沿b方向作用的弯矩设计值Mb为20N·m，沿h方向作用的弯矩设计Mh值为24kN·m，试验算该柱的承载力是否满足安全性要求。

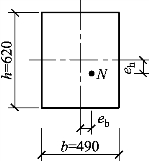
图5.43　例5.6图

【解】　（1）求A值。

A=0.49×0.62=0.303 8(m2)＞0.3(m2)

（2）求偏心距eb、eh。

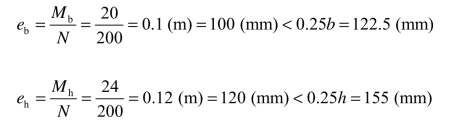
（3）求附加偏心距eib、eih。

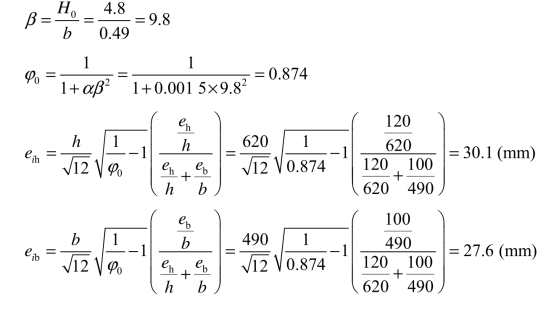
（4）求f值。

査表5.7得砌体抗压强度设计值为1.69N/mm2。

（5）求φ值。

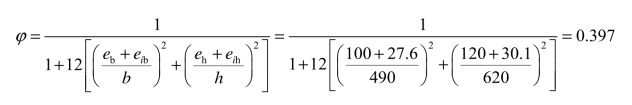
（6）承载力验算。

φfA=0.397×1.69×0.303 8×103＝204(kN)＞200(kN)

该柱的承载力满足安全性要求。