【例3.4】 某工业建筑多层仓库,楼盖平面如图3.38所示。楼层高4.5m,采用钢筋混凝土整浇楼盖,试设计。
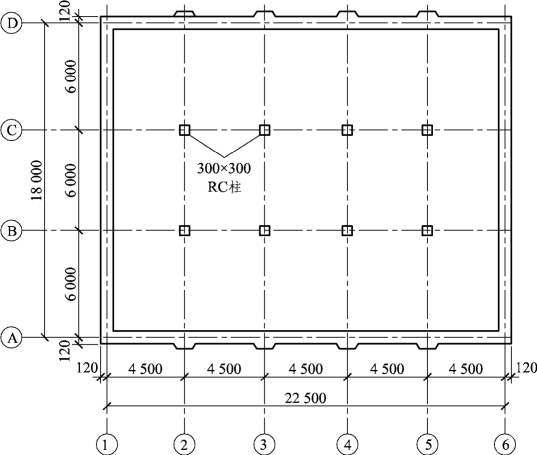
图3.38 某工业建筑多层仓库楼盖平面
一、设计资料
1.楼面做法
20mm水泥砂浆面层;钢筋混凝土现浇板;12mm纸筋石灰抹底。
2.楼面活荷载
楼面均布活荷载标准值:8.0kN/m2。
3.材 料
混凝土强度等级C25;梁内受力主钢筋为HRB335级钢筋,箍筋采用HPB300级钢筋,板筋采用HPB300级钢筋。
二、楼面梁格布置及截面尺寸
1.梁格布置
梁格布置见图3.39。主梁、次梁的跨度分别为6m和4.5m,板的跨度为2m。
主梁沿横向布置,每跨主梁均承受两个次梁传来的集中力,梁的弯矩图较平缓,对梁工作有利。
由图3.39可见,板区格长边与短边之比4.5/2=2.25>2.0但<3.0,按规范规定宜按双向板计算,本例题按单向板计算,并采取必要的构造措施。
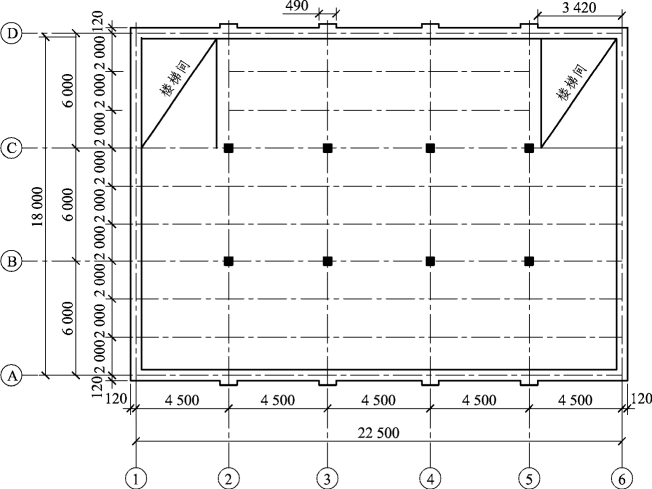
图3.39 梁格布置
2.截面尺寸
因结构的自重和计算跨度都和板的厚度、梁的截面尺寸有关,故应先确定板、梁的截面尺寸。
(1)板:按刚度要求,连续板的厚度取
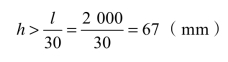
工业建筑楼板的最小厚度为70mm,本例考虑楼盖活荷载较大,故取h=80mm。
(2)次梁:截面高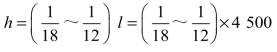 =250~375mm,取h=400mm
=250~375mm,取h=400mm
截面宽b=200mm
(3)主梁:截面高![]() =430~750mm,取h=600mm
=430~750mm,取h=600mm
截面宽b=250mm
三、板的设计
按考虑内力重分布方法进行。
1.荷载计算(表3.12)
表3.12 板的荷载计算

楼面均布活荷载因标准值大于4.0kN/m2,故荷载分项系数γG=1.3,则1m宽板带上的荷载:
由可变荷载效应控制的组合g+q=(1.2×2.6+1.3×8.0)×1=13.52(kN/m)
由永久荷载效应控制的组合g+q=(1.35×2.6+0.7×1.3×8.0)×1=10.79(kN/m)
可见,对板而言,由可变荷载效应控制的组合所得荷载设计值较大,所以板内力计算时取g+q=13.52(kN/m)。
2.计算简图
计算跨度:因次梁截面为200mm×400mm,则

因l01与l02相差极小,故可按等跨计算,且近似取计算跨度l0=1 800mm,如图3.40。
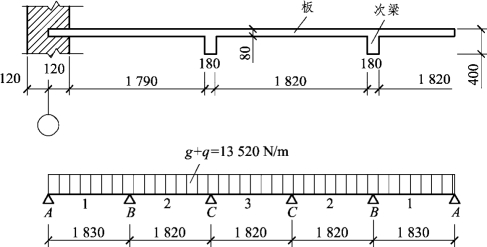
图3.40 板的计算简图
3.弯矩设计值

4.配筋计算
板厚h=80mm,h0=80-20=60mm;C25混凝土的强度fc=11.9N/mm2;HPB300级钢筋fy=270N/mm2。
轴线②~⑤间的板带,其四周均与梁整体浇筑,故这些板的中间跨及中间支座的弯矩均可减少20%(表3.13中括号内数值),但边跨及第一内支座的弯矩(M1及MB)不予减少。
最小配筋率为max(0.2,45ft/fy)%=0.21%,最小配筋面积As,min=0.21%×1 000×80=168mm2。
表3.13 板的配筋计算

(1)选配钢筋。
对轴线②~⑤之间的板带,第一跨和中间跨板底钢筋各为φ8@180和φ6@160,此间距小于200mm,且大于70mm,满足构造要求。对中间支座受力钢筋,为了防止钢筋过细而施工时被踩下,也可取直径为8mm,间距200mm(As=251mm2)。
(2)受力钢筋的截断。
本设计采用分离式配筋,支座上部受力钢筋的切断距离,当q/g=10 400/3 120=3.3>3时,应取a=ln/3=1 820/3≈600mm,上部钢筋应用直钩下弯顶住模板以保持其有效高度。
(3)钢筋锚固。
下部受力纵筋伸入支座内的锚固长度la为:边支座要求大于5d及50mm,现浇板的支承宽为120mm,故实际la=120-10=110mm,满足要求;中间支座la=100mm(=b/2)>5d及50mm。
(4)构造钢筋。
分布筋用φ6@200,板配筋图略。
(5)板截面受剪承载力验算。
板截面受剪承载力可按式(3.19)计算,最大剪力设计值发生在离端第二支座左侧,其值为:
V=0.6×13.52×1.78=14.44(kN)<0.7βhftbh0=0.7×1×1.27×1 000×60=53.34(kN)故满足要求。
四、次梁设计
按考虑内力重分布方法进行。根据本楼盖的实际使用情况,作用于次梁、主梁上的活荷载一律不考虑折减,即取折减系数为1.0。
1.荷载计算(表3.14)
表3.14 次梁的荷载计算
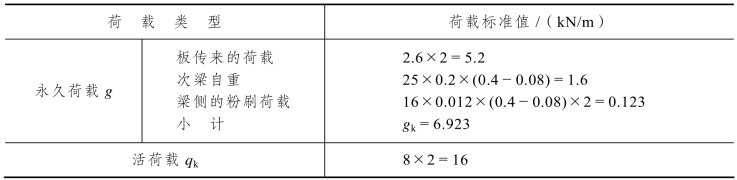
由可变荷载效应控制的组合:g+q=1.2×6.923+1.3×16=29.11(kN/m)
由永久荷载效应控制的组合:g+q=1.35×6.923+0.7×1.3×16=23.906(kN/m)所以次梁内力计算时取g+q=29.11(kN/m)。
2.计算简图
次梁按考虑塑性内力重分布方法计算内力,其计算跨度如下。
次梁在砌体上支承宽度为240mm,故:
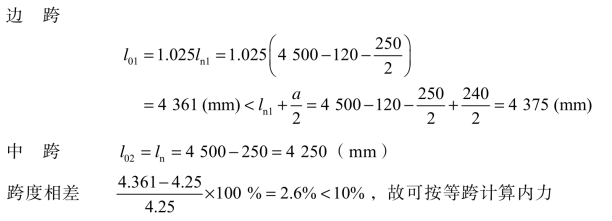
计算简图如图3.41。
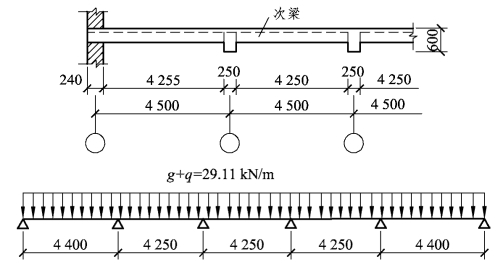
图3.41 次梁的计算简图
3.内力计算
设计弯矩:
![]()
此处支座弯矩应按相邻两跨中较大跨长计算。
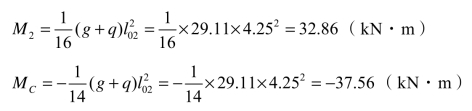
设计剪力:
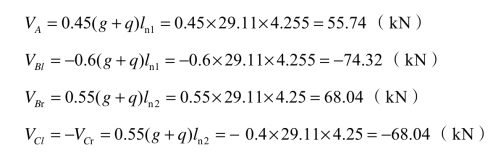
4.正截面承载力计算(表3.15)
(1)次梁的跨内截面应考虑板的共同作用而按T形截面计算,其翼缘的计算宽度![]() 可按表3.10中的最小值确定。
可按表3.10中的最小值确定。
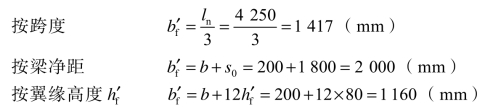
取![]() =1 160mm计算。
=1 160mm计算。
(2)判别T形截面类型:

属第I类T形截面。
梁纵向受力钢筋最小配筋率为max(0.2,45ft/fy)%=0.20%,最小配筋面积As,min=0.20%×200×400=160(mm2)。
表3.15 次梁正截面配筋计算
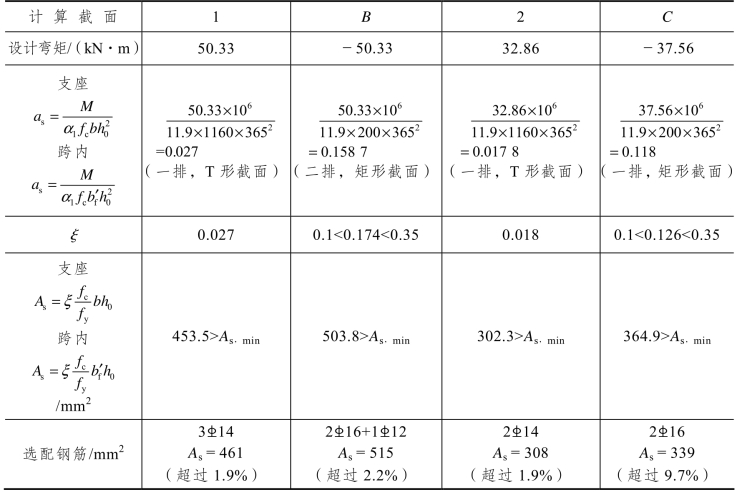
①各截面的实际配筋往往和计算需要量有出入,一般误差以不超过±5%为宜,有困难时应尽量满足不超过±10%。
②纵筋的截断:当次梁跨长相差在20%以内,且q/g=20.8/8.307=2.50<3时,可按图3.35的原则确定钢筋的截断位置,具体构造见图3.42。
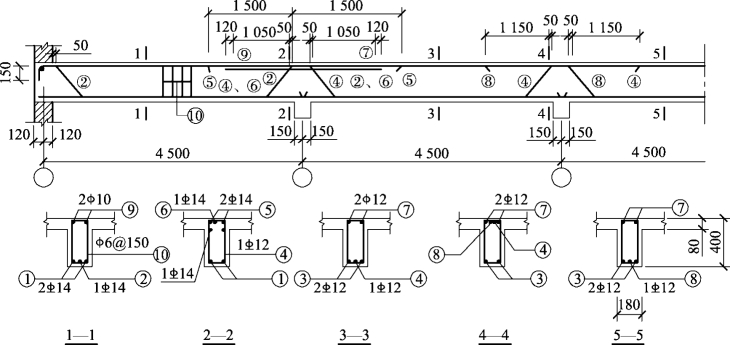
图3.42 次梁的截面配筋
上部纵筋:③号钢筋为1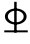 16钢筋,其左侧钢筋截断点距B支座边缘距离为1 200m>ln/5+20d=1 091mm,其截断面积为113.1mm2<0.5×515=257.5mm2,符合要求;同理,可检验③号筋在B支座右侧钢筋截断点满足要求。
16钢筋,其左侧钢筋截断点距B支座边缘距离为1 200m>ln/5+20d=1 091mm,其截断面积为113.1mm2<0.5×515=257.5mm2,符合要求;同理,可检验③号筋在B支座右侧钢筋截断点满足要求。
下部纵筋:②号钢筋伸入A支座长度为200mm>12d=12×14=168mm,④号纵筋伸入B支座长度为200mm>12d=12×14=168mm,满足要求。
③根据规范要求,梁宽为200mm时,至少应采用2根上部钢筋贯通。此例中各跨均用2 16受力纵筋兼做架立筋以简化施工。
16受力纵筋兼做架立筋以简化施工。
5.斜截面强度计算
(1)复核梁截面尺寸。
0.25fcbh0=0.25×11.9×200×365=217(kN)>VBC=74.32(kN)
故截面尺寸符合要求。
(2)验算是否需按计算配置腹筋。
A支座:VA=55.74(kN)<0.7ftbh0=0.7×1.27×200×365=64.90(kN)(https://www.xing528.com)
应按构造配置横向钢筋。
取箍筋双肢φ6@150mm,则

B支座左侧:VBl=74.32(kN)>0.7ftbh0=64.90(kN)
应按计算配置横向钢筋,取箍筋双肢φ6,则

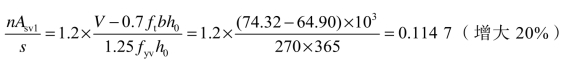
B支座右侧及C支座计算过程同B支座左侧,最后均取双肢φ6@150mm。
五、主梁设计
1.荷载计算(表3.16)
主梁除承受由次梁传来的集中荷载(包括板、次梁上的永久荷载和作用在楼盖上的活荷载)外,还有主梁的自重。主梁的自重实际是均布荷载,但为了简化计算,可近似将2m长度的自重按集中荷载考虑。
表3.16 主梁的荷载计算
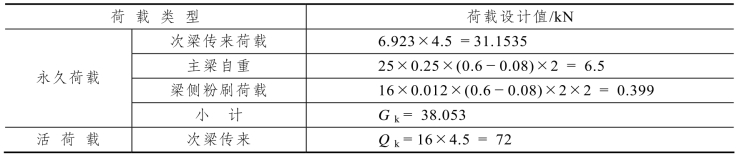
永久荷载设计值:G=1.2×38.053=45.7(kN)
或 1.35×38.053=51.4(kN)
可变荷载设计值:Q=1.3×72=93.6(kN)
或 0.7×1.3×72=65.52(kN)
2.计算简图
主梁内力计算按弹性方法进行,如图3.43所示。
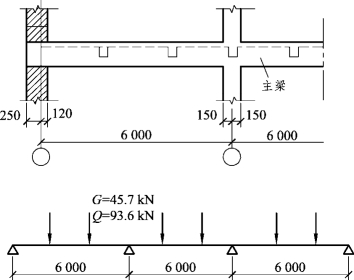
图3.43 主梁的计算简图
计算跨度为:
边 跨 l01=6.0-0.12+![]() =6.065(m)
=6.065(m)
又 1.025ln1+0.15=1.025×(6-0.15-0.12)+0.15=6.02(m)
应取 l01=6.02m
中 跨 l02=6.0m
因计算跨度相差甚少,故一律用6.0m计算。
因柱截面为300mm×300mm,楼层高度为4.5m,经计算梁柱线刚度比约为5,此时主梁的中间支承可近似按铰支座考虑。
3.内力计算
根据主梁的计算简图及荷载情况,可求得各控制截面的最不利内力。详见表3.17。
表3.17 最不利内力计算

由各种荷载布置情况下的内力计算,得出相应的内力图,叠加这些内力图,得如图3.44所示弯矩、剪力的叠合图,该图较好地反映了主梁的内力情况。现以主梁各控制截面的最不利内力进行配筋计算。
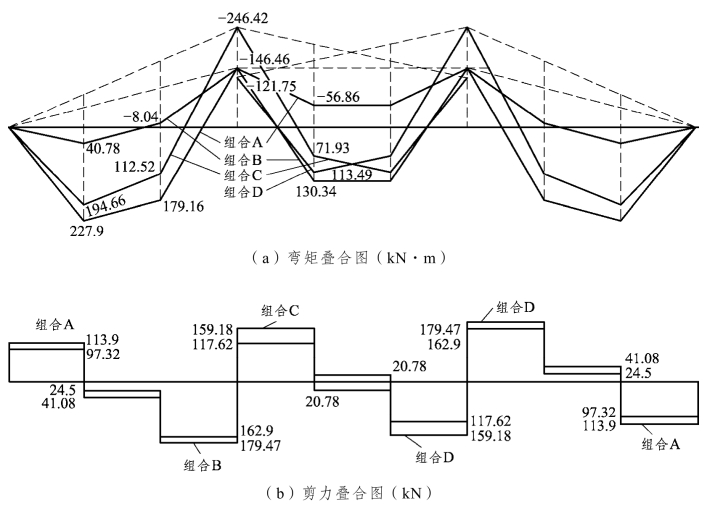
图3.44 弯矩、剪力叠合图
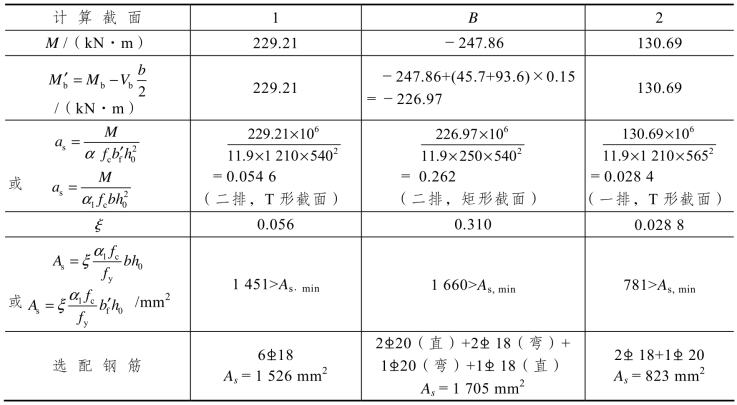
4.主梁正截面承载力计算(表3.18)
(1)确定跨内翼缘计算宽度![]() 。
。

故取翼缘计算宽度![]() =1 210mm。
=1 210mm。
(2)判别T形截面类型:
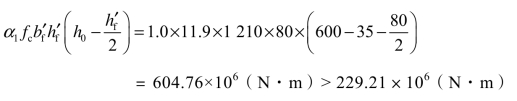
知属第I类T形截面。
梁纵向受力钢筋最小配筋率为max(0.2,45ft/fy)%=0.20%,最小配筋面积As,min=0.20%×250×600=300(mm2)。
表3.18 主梁正载面配筋计算
5.斜截面承载力计算
(1)复核梁截面尺寸。
因hw/b=520/250=2.08<4,属一般梁,取
0.25fcbh0=0.25×11.9×250×540=401.6×103(N)>VBl=180.61(kN)(最大剪力)
故截面尺寸满足要求。
(2)验算是否需按计算配置横向钢筋。
A支座:0.7ftbh0=0.7×1.27×250×565=125.57(kN)>VA=114.6(kN)
应按构造配置横向钢筋。
B支座左:0.7ftbh0=0.7×1.27×250×540=120(kN)<VBl=180.61(kN)
应按计算配置横向钢筋。
B支座右:0.7ftbh0=0.7×1.27×250×540=120(kN)>VBr=160.10(kN)
应按计算配置横向钢筋。
(3)横向钢筋计算。
采用φ8@200双肢箍筋,间距小于smax=250mm,配箍率:

验算支座A:

验算支座B:
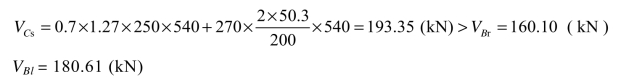
知支座B配置箍筋φ8@200已能满足斜截面受剪要求,弯起钢筋可按构造处理。本例中因VCs与VBl接近,支座B左侧的弯起钢筋偏安全仍按计算需要布置。因主梁受集中荷载,剪力图呈矩形,故在2m范围内应布置3道弯起筋,以便覆盖此最大剪力区段。
(4)主梁吊筋计算。
由次梁传给主梁的集中荷载:
由可变荷载效应控制的组合:Fl=1.2×31.1535+1.3×72=130.98(kN)
由永久荷载效应控制的组合:Fl=1.35×31.1535+0.7×1.3×72=107.588(kN)
Fl中未计入主梁自重及梁侧粉刷重,取130.98kN。设附加φ8双肢箍筋,只设箍筋时

所需箍筋个数:485.1/(2×50.3)=4.8个,实取6个。此箍筋的有效分布范围s=2h1+3b=2×150+3×250=1 050(mm),取6个φ8@100mm,次梁两侧各3个。
6.配筋布置
支座B根据斜截面受剪承载力的要求,于第一跨先后弯起2 18。第二跨可弯起1
18。第二跨可弯起1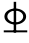 20,则支座截面可计入2
20,则支座截面可计入2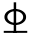 18+1
18+1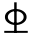 20承担支座负弯矩。按正截面强度计算尚需增加2
20承担支座负弯矩。按正截面强度计算尚需增加2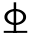 20+1
20+1 18直钢筋,满足B支座钢筋面积要求,且满足主梁3个控制截面的实际配筋量与计算的差值应尽量不超过±5%。
18直钢筋,满足B支座钢筋面积要求,且满足主梁3个控制截面的实际配筋量与计算的差值应尽量不超过±5%。
7.绘制抵抗弯矩图
前面根据主梁各跨内和支座最大(绝对值)计算弯矩确定出所需钢筋数量,而其他各截面需要的钢筋量将比控制截面少,这样就需要根据梁弯矩包络图,将控制截面的纵筋延伸至适当位置后,把其中的部分钢筋弯起或截断。主梁纵筋的弯起或截断位置可以通过绘制抵抗弯矩图(又称材料图)的方法来解决。抵抗弯矩图的实质是用图解的方法确定梁各正截面所需钢筋的数量。
1)钢筋能承担的极限弯矩
按实际配置的钢筋面积Asc计算出控制截面上材料能承担的极限弯矩。此时可忽略截面上内力臂值的某些差别。这些差别由钢筋实配面积与计算差异引起,包括同一截面中位于第一排和第二排钢筋间的内力臂差别。现将同一截面各纵筋的计算内力臂值取为相同,这样实配钢筋的极限弯矩为MC=(Asc/As) M,而每一根钢筋所承担的极限弯矩仅与其截面面积成正比。
例如支座B的计算弯矩为226.97kN·m,计算所需钢筋面积为As=1 660mm2。实配钢筋面积Asc=1 705mm2,则其极限弯矩:
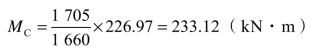
其中1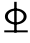 18与1
18与1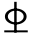 20钢筋所能承担的极限弯矩:
20钢筋所能承担的极限弯矩:
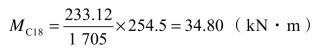

采用与弯矩叠合图相同的比例在支座计算截面沿纵向量取MC=233.12kN·m,按每根钢筋所能承担的极限弯矩沿纵标分段,自分段点作弯矩图基线的平行线,并与弯矩包络图相交。如支座左侧的⑥号筋,其划分MC20的两根平行线与包络图的上交点,指示出该钢筋被充分利用的截面;其下交点处则为该钢筋按正截面强度计算已完全不需要,是⑥号筋的理论截断点。
2)钢筋的弯起和截断顺序
在具体作抵抗弯矩图前,应初步确定截面上每一根钢筋的“走向”和弯起或截断顺序:当截面上有两排钢筋时,宜将第二排先弯起或截断;在同一排中宜先弯起或截断位于中间位置的钢筋。应使钢筋在截面中线两边尽量对称,不能让钢筋重心过分偏于截面中线的一边。抵抗弯矩图宜靠近弯矩图,但不能插入(允许少5%)。例如支座B左侧为了使满足斜截面抗剪要求所布置的2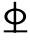 18弯起钢筋能覆盖最大剪力区段,故它们的弯起点已基本确定。在考虑了上述原则后,弯筋的下弯顺序为④、③,直钢筋的截断次序为⑤、⑥。直钢筋的具体截断点在绘制抵抗弯矩图时确定。
18弯起钢筋能覆盖最大剪力区段,故它们的弯起点已基本确定。在考虑了上述原则后,弯筋的下弯顺序为④、③,直钢筋的截断次序为⑤、⑥。直钢筋的具体截断点在绘制抵抗弯矩图时确定。
3)钢筋的截断
例如支座B左侧的⑥号钢筋,因此处V>0.7ftbh0,故钢筋截断应从该钢筋强度充分利用截面延伸出1.2la+h0。此处 la为受拉钢筋的锚固长度。对C25、HRB335级钢筋,la=αfy/ft得la=33d。⑥号钢筋d=20mm,故延伸长度为1.2×33×20+540=1 332(mm)。反映在图3.42的抵抗弯矩图上则应从⑥号钢筋按正截面抗弯能力计算不需要截面(即理论截断点)以外1 150mm处,此值大于20d,满足要求。其余钢筋的截断同此。
4)钢筋的弯起
③号筋在距其强度充分利用截面350mm处下弯,此距离大于h0/2,故能计入其抗弯能力。斜筋在梁轴线以上的区段参加抵抗负弯矩的作用,梁轴线以下斜段则进入抵抗正弯矩,故每一根弯筋在材料图上的正、负弯矩图上均应有对应的反映。
5)架立筋
根据规范要求,梁宽b=300mm时,应至少选取2根上部钢筋作为架立筋。本例中,选用2 20即①号受力筋兼做架立筋。
20即①号受力筋兼做架立筋。
6)侧面构造钢筋
根据规范要求,当 hw≥450mm时,宜在梁每侧沿梁高每隔200mm设置构造钢筋,来抵御扭矩及混凝土收缩和温度应力的影响,本例中设置4 12钢筋作为侧面构造钢筋,同时使用φ8@400构造箍筋,以增强侧面构造钢筋联系。
12钢筋作为侧面构造钢筋,同时使用φ8@400构造箍筋,以增强侧面构造钢筋联系。
7)纵筋的锚固
支座A按简支考虑,其上部弯起筋和架立筋的锚固要求见图3.45。下部纵筋伸入梁的支座范围应满足锚固长度las≥12d,即12×18=216mm<370mm,满足要求。
支座B下部纵筋的锚固问题,从图3.46可见,该处计算中已不利用下部纵筋,故其伸入的锚固长度las≥12d,现取为300mm,满足要求。
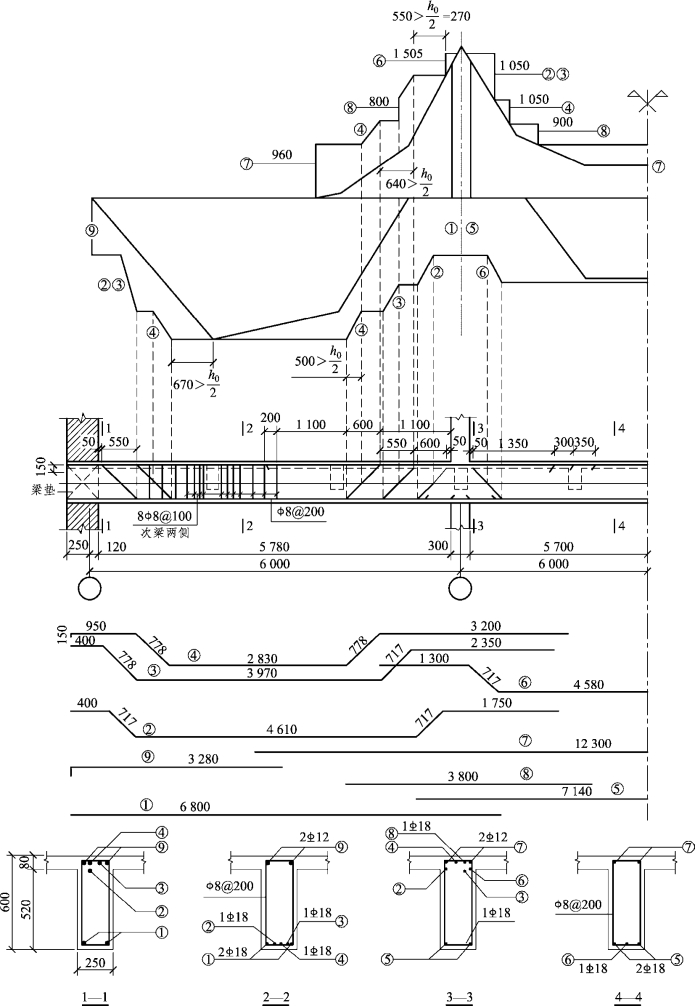
图3.45 主梁的截面配筋

图3.46 纵筋的锚固
8.梁 垫
为满足砌体局部受压的承载力要求,主梁的端支承处设有混凝土垫块,垫块与梁浇成整体。相关计算此处从略。
主梁的配筋详见图3.45,纵筋的锚固详见图3.46。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




