单向板肋梁楼盖的弹性理论计算方法

钢筋混凝土现浇楼盖通常为梁、板组成的超静定结构，其内力可按弹性理论及塑性理论进行分析。按塑性理论分析内力，使结构内力分析与构件截面承载力计算相协调，结果比较符合实际且比较经济，但会使结构的裂缝较宽，变形也较大。《混凝土结构设计规范》规定：混凝土连续梁和连续单向板，可采用塑性内力重分布方法进行分析。重力荷载作用下的框架、框架-剪力墙结构中的现浇梁以及双向板等，经弹性分析求得内力后，可对支座或节点弯矩进行适当调幅，并确定相应的跨中弯矩。

楼盖结构按弹性理论及塑性理论进行分析时，可根据计算精度要求，采用精细分析方法或简化分析方法。精细分析方法包括弹性理论、塑性理论方法以及线性和非线性有限元分析方法。简化分析方法是在一定假定基础上建立的近似方法，可分为以下两种：

（1）假定支承梁的竖向变形很小，可以忽略不计，将梁、板分开计算。此法根据作用于板上的荷载，按单向板或双向板计算板的内力，然后按照假定的荷载传递方式，将板的上荷载传到支承梁上，计算到承梁的内力。包括基于弹性理论的连续梁、板法（用于计算单向板肋梁楼盖），查表法和多跨连续双向板法（用于计算双向板肋梁楼盖），以及基于塑性理论的弯矩调幅法和基于板破坏模式（假定支承梁未破坏）的塑性极限分析方法。

（2）考虑梁、板的相互作用，按楼盖结构进行分析。此法根据作用于楼盖上的荷载，将楼盖作为整体计算梁和板的内力。包括基于弹性理论的直接设计法、等效框架法和拟梁法等，以及基于塑性理论和梁-板组合破坏模式（支承梁可能破坏）的塑性极限分析方法。这种分析方法考虑了梁、板的相互作用，可用于计算无梁楼盖以及支承梁刚度相对较小的肋梁楼盖的内力，此法适用于柱支承板楼盖结构的设计。

按弹性理论的计算是指在进行梁（板）结构的内力分析时，假定梁（板）为理想的弹性体，可按“结构力学”的一般方法进行计算。

1.计算简图的确定

楼盖结构是由许多梁和板构成的平面结构，承受竖向的自重和使用活荷载。由于板的刚度很小，次梁的刚度又比主梁的刚度小很多，因此可以将板看作被简单支承在次梁上的结构部分，将次梁看作被简单支承在主梁上的结构部分，则整个楼盖体系即可以分解为板、次梁和主梁几类构件单独进行计算。

作用在板面上的荷载传递路线为：荷载→板→次梁→主梁→柱（或墙）。它们均为多跨连续梁，其计算简图应表示出梁（板）的跨数、计算跨度、支座的特点以及荷载形式、位置及大小等。

1）计算单元

为减少计算工作量，结构内力分析时，常常不是对整个结构进行分析，而是从实际结构中选取有代表性的一部分作为计算的对象，称为计算单元。

对于单向板，一般沿跨度方向取lm宽度的板带作为其计算单元，在此范围内，即图3.17中用阴影线表示的楼面均布荷载便是该板带承受的荷载，这一负荷范围称为从属面积，即计算构件负荷的楼面面积。

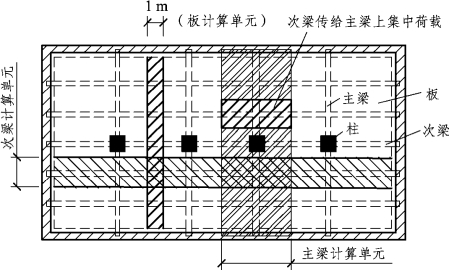
图3.17　单向板肋梁楼盖板、梁计算单元

次梁：计算单元宽度取相邻次梁中心距的一半。

主梁：计算单元宽度取相邻主梁中心距的一半。

2）支座条件的假定与计算简图

支座条件的假定对计算简图有着直接的影响，如图3.18所示。

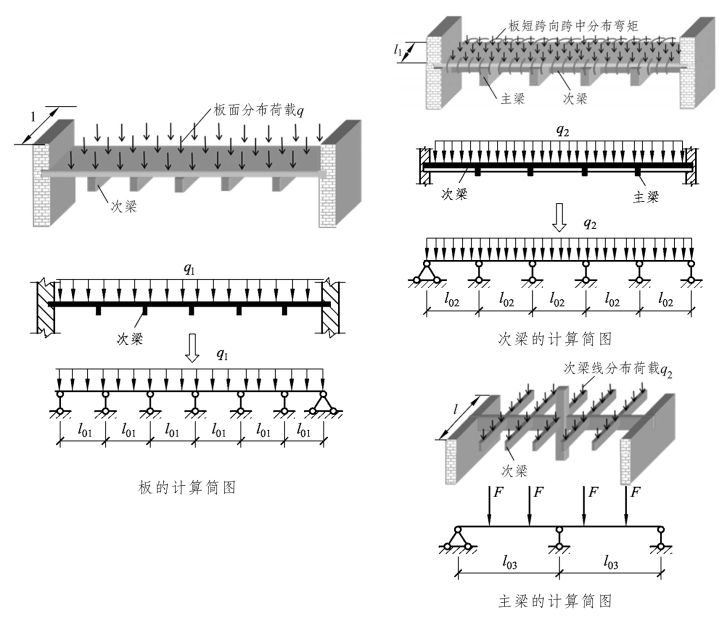
图3.18　单向板肋梁楼盖板、梁计算简图

（1）板：单向板是沿跨度方向取1m宽度的板带作为其计算单元，板带有两类边界：板带（单元）之间以及板带与次梁（或支承墙）之间。因单向板忽略长跨向内力，所以板带之间的边界可作为自由边；当板或梁支承在砖墙（或砖柱）上时，由于其嵌固作用较小，可假定为铰支座，其嵌固的影响可在构造设计中加以考虑。次梁对板在该处的竖向位移和转角位移有约束；如果忽略竖向位移和转动约束，板可以简化为连续梁计算简图。

（2）次梁单元之间的边界上有分布力矩作用，无剪力；但这些分布力矩对次梁轴线方向的内力没有影响；次梁与主梁的边界与板与次梁的边界类似；在相同的假定下，次梁也可以简化为连续梁计算简图。

（3）主梁的计算简图应根据梁与柱的线刚度比值而定。当梁柱节点两侧梁的线刚度之和与节点上下柱的线刚度之和的比值大于3时，柱的线刚度相对较小，柱对主梁的转动约束不大，可将柱子作为主梁的不动铰支座。主梁的计算简图也可以按连续梁。

当梁、柱的线刚度之和的比值小于3时，则应考虑柱对主梁的转动约束作用，这时应按框架结构来进行内力分析，如果主梁尚需与竖向构件一起共同承担水平作用（如风载、地震作用等），也应按框架梁计算。

3）计算跨度

计算跨度，是指梁、板设计进行内力计算时采用的跨度。理论上的计算跨度指的是相邻支座反力间的距离，它与支座构造形式、支在墙上的支承长度及内力计算方法有关。准确确定非常复杂，工程中一般按如下取值：

（1）按弹性理论计算时：中间各跨取支承中心线之间的距离；边跨如果端部搁置在支承构件上，则：对于梁，边跨计算长度在（1.025ln1+b/2）与[ln1+(a+b)/2]两者中取小值；对于板，边跨计算长度在（1.025ln1+b/2）与[ln1+(h+b)/2]两者中取小值；梁、板在边支座与支承构件整浇时，边跨也取支承中心线之间的距离。

（2）按塑性理论计算时：当内支座与被支承构件整体连接时，由于塑性铰出现在支承边，中间各跨计算长度取净跨ln；当内支座被支承构件搁置在支承构件上时，由于塑性铰出现在支承中心处，中间各跨计算长度取支承中心线之间的距离。塑性铰位置如图3.19所示。

边跨端部搁置在支承构件上时取值方法同弹性理论。

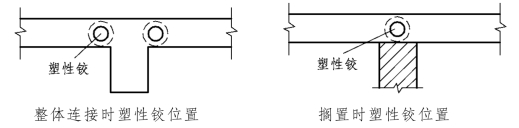
图3.19　塑性铰位置示意

板和梁的计算跨度如表3.7所示。

表3.7　连续板梁的计算跨度

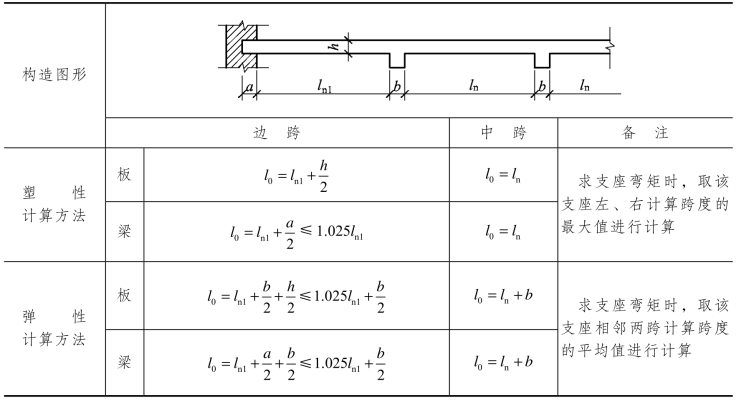
实际工程中梁、板各跨的跨度往往是不同的。当手算内力时，为了简化计算，假定当相邻跨度相差 ≤10%时，仍按等跨计算，这时支座弯矩按相临两跨跨度的平均值计算。

4）计算跨数

不论对板或梁，当各跨荷载相同，而跨数超过5跨的等截面与等跨度连续板、梁，除靠近端部的第1、2两跨外，其余的中间跨内力都十分接近。为简化设计，工程上可将中间各跨内力均取与第3跨相同。故当跨数≤5时，按实际跨数考虑；当跨数＞5时，可近似按5跨考虑。配筋计算时除两端的两边跨外，中间各跨配筋相同。

5）计算荷载

（1）荷载取值

楼盖上的荷载有恒荷载和活荷载两类。恒荷载包括结构自重、建筑面层、固定设备等。活荷载包括人群、堆料和临时设备等。恒荷载的标准值可按其几何尺寸和材料的重力密度计算。民用建筑楼面上的均布活荷载标准值可以从《建筑结构荷载规范》中查得。工业建筑楼面活荷载，在生产、使用或检修、安装时，由设备、管道、运输工具等产生的局部荷载，均应按实际情况考虑，可采用等效均布活荷载代替。

对于单向板，其计算单元范围内的楼面均布荷载便是该板带承受的荷载，这一负荷范围称为从属面积，即计算构件负荷的楼面面积（图3.17）。

次梁的荷载为次梁自重及左右两侧板传来的均布荷载。计算板传给次梁的荷载时，不考虑板的连续性，即板上的荷载平均传给相邻的次梁（图3.17）。

主梁的荷载是主梁自重和次梁传来的集中荷载。为了简化计算，将主梁自重也作为集中荷载处理。作用在主梁上的主梁自重集中荷载的个数及作用点位置与次梁传来的集中荷载的个数和作用位置相同，每个主梁自重集中荷载值等于长度为次梁间距的一段主梁自重。计算次梁传给主梁的集中荷载时，也不考虑次梁的连续性，即主梁承担相邻次梁各1/2跨的荷载（图3.17）。

（2）板和次梁的折算荷载

以上对板和次梁所取的计算简图是连续梁，即假定板或梁支承在不动的铰支座上。实际次梁对板，主梁对次梁将有一定的嵌固作用，按弹性理论计算时须考虑约束影响。

当板的支座是次梁，次梁的支座是主梁，则当板承受荷载而变形时，次梁发生扭转。由于次梁的两端被主梁所约束及次梁本身的侧向抗扭刚度影响，所以板的挠度大大减少，使板在支承处的实际转角θ′比理想铰支承时的转角θ小，如图3.20所示。同样的情况发生在次梁和主梁之间。考虑次梁对板、主梁对次梁转动约束作用的有利影响，按弹性理论计算时，通常采用减少活荷载增加恒荷载的方法进行调整处理，即以“折算荷载”代替实际计算荷载。又由于次梁对板的约束作用较主梁对次梁的约束作用大，故对板和次梁采用不同的调整幅度。调整后的折算荷载取为：

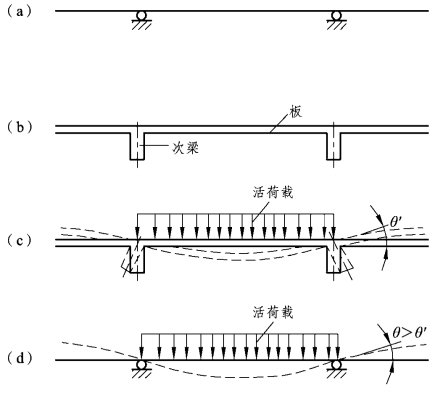
图3.20　支座抗扭刚度的影响

对于板：

对于次梁：

式中：g、q分别为实际均布恒荷载、均布活荷载；g′、q′分别为折算均布恒荷载、均布活荷载。

主梁不进行荷载折算。这是因为当柱刚度较小时，柱对梁的约束作用很小，可忽略其影响。

2.活荷载最不利布置

因可变荷载的位置是变化的（活荷载是以一跨为单位来改变其位置的），因此在设计连续梁、板时，应研究活荷载如何布置将使梁、板内某一控制截面上的内力绝对值最大，这种布置称为活荷载的最不利布置。

1）活荷载作用于不同跨时的弯矩图和剪力图

由弯矩分配法知，某一跨单独布置活荷载时：①本跨支座为负弯矩，相邻跨支座为正弯矩，隔跨支座又为负弯矩；②本跨跨中为正弯矩，相邻跨跨中为负弯矩，隔跨跨中又为正弯矩。

根据前面确定的计算简图，为了充分认识活荷载的不利布置，取常用的五跨连续梁分析活荷载位置变化时连续梁的内力变化情况，如图3.21所示。

(www.xing528.com)

图3.21　连续梁的内力变化

2）最不利活载布置原则

通过对图3.21的内力变化规律分析，利用叠加原理，并考虑活载的特点（可以某一跨有荷载，也可以某两跨、三跨有荷载），以某一控制截面内力最大为目标，确定最不利活载布置，最后得其布置原则如下：

（1）求某跨跨中最大正弯矩时，应在该跨布置活载，然后隔跨布置。

（2）求某跨跨中最大负弯矩（或最小弯矩）时，该跨不布置活载，而在左、右相邻两跨布置活载，然后隔跨布置活载。

（3）求某支座最大负弯矩时，或求某支座左、右截面最大剪力时，应在该支座左右两跨布置活载，然后隔跨布置。

3）连续梁活荷载最不利布置图

根据上面的原则，对常用的五跨连续梁，可得各控制截面上最大内力的活载和恒载布置，如图3.22所示。

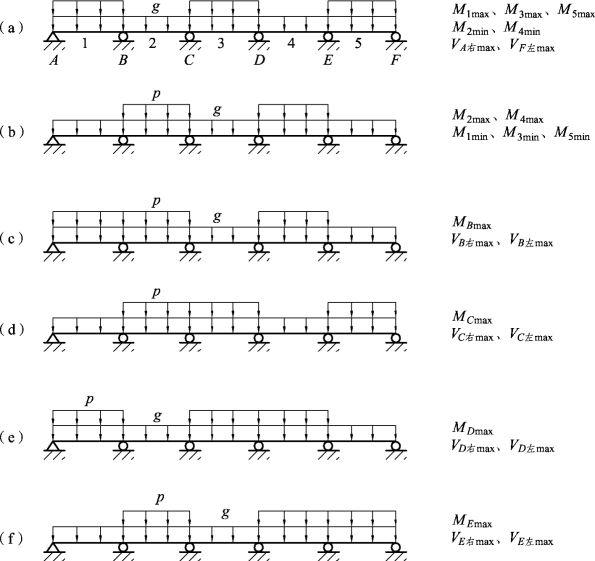
图3.22　各控制截面最大内力的荷载布置

3.弹性内力计算

有了等跨连续梁的计算简图，有了梁上的恒载、活载及其活载不利布置后，就可以按结构力学方法进行连续梁的内力计算。计算时注意叠加原理的运用。两跨至五跨的等跨连续梁在各种基本荷载作用下的内力，有许多建筑结构静力计算手册可查（附表3.1中列出了一部分），计算时可直接查用。由附表3.1可直接查得各种荷载布置情况下的内力系数，求等跨连续梁某控制截面内力时，按下面各式计算。

（1）在均布荷载及三角形荷载作用下：

（2）在集中荷载作用下：

（3）内力正负号规定：

M：使截面上部受压、下部受拉的弯矩为正，反之为负。

V：在构件上取单元体，使单元体产生顺时针转动的剪力为正，反之为负。

控制截面：通常指控制构件配筋的截面，也是内力最大的截面。

【例3.1】　如图3.23（a）所示，某两跨连续梁上，作用有恒载设计值g＝5kN/m，活载设计值p＝15kN/m，求各控制截面内力。

【解】　根据活载布置不同有4种情况。

（1）当活载满布时，连续梁上荷载q＝g+p＝5+15＝20kN/m，查附表3.1.1有：

M1＝M2＝0.070ql2＝0.07×20×62＝50.4（kN·m）

MB＝-0.125ql2＝-0.125×20×62＝-90（kN·m）

VA右＝-VC左＝0.375ql2＝45（kN）

VB右＝-VB左＝0.625ql＝-75（kN）

（2）当活载p只作用在AB跨时，可以把连续梁看成是由满布荷载g和只在AB跨作用的活载p两种情况叠加。利用附表3.1.1中内力系数直接计算有：

M1＝0.07gl2+0.096pl2＝0.07×5×62+0.096×15×62＝64.44（kN·m）

M2＝0.070 3gl2+1/2×(-0.063)pl2＝-4.356（kN·m）

MB＝-0.125gl2-0.063pl＝-0.125×5×62-0.063×15×62＝-56.52（kN·m）

VA右＝0.375gl+0.437pl＝50.58（kN）

VC左＝-0.375gl+0.063pl＝-5.58（kN）

VB右＝0.625gl+0.063pl＝24.42（kN）

VB左＝-0.625gl-0.563pl＝-69.42（kN）

（3）当活载p只作用在BC跨时，由结构对称性可知，这时连续梁内力和（2）是对称的。

（4）当只有恒载作用时，连续梁内力为：

MB＝-0.125gl2＝-0.125×5×62＝-22.5（kN·m）

M1＝M2＝0.07gl2＝0.07×5×62＝12.6（kN·m）

VA右＝-VC左＝0.375gl＝11.25（kN）

VB右＝-VB左＝0.625gl＝18.75（kN）

将上面（1）～（4）四种荷载布置情况下的内力画在同一个图上，如图3.23（b）、（c）所示。

4.内力包络图

根据各种最不利荷载组合，按一般结构力学方法或利用前述表格进行计算，即可求出各种荷载组合作用下的内力图（弯矩图和剪力图），把它们叠画在同一坐标图上（用同样比例画在同一个图上），其外包线所形成的图形称为内力包络图，它表示连续梁在各种荷载最不利布置下各截面可能产生的最大内力值。连续梁的弯矩包络图和剪力包络图是确定连续梁纵筋、弯起钢筋、箍筋的布置和绘制配筋图的依据。

图3.23（b）、（c）就是例题3.1中四种荷载组合下的内力图叠加，其外包线就是内力包络图。

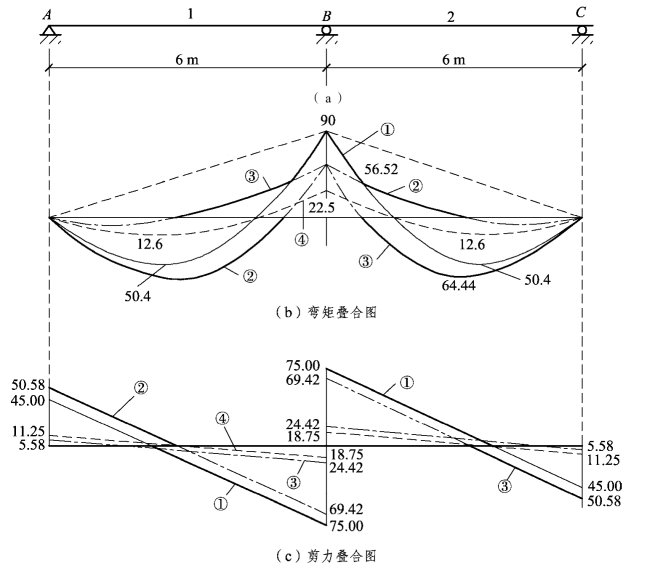
图3.23　两跨连续梁弯矩和剪力

【例3.2】　图3.24所示两跨连续梁，跨度为4m，承受恒载G＝10kN，活载P＝10kN，均作用于跨中，求该梁的内力包络图。

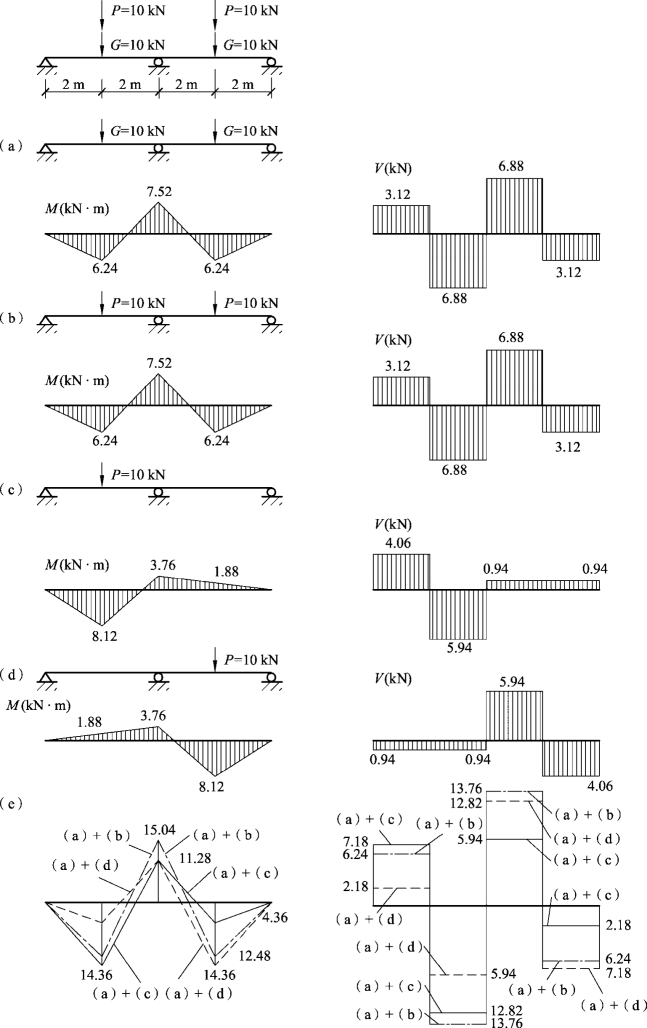
图3.24　两跨连续梁内力包络图

【解】　由题意可知，活载布置有3种情况，即分别使中间支座、左跨中、右跨中截面弯矩最大。而内力计算图示有2种情况，即一跨有荷载和两跨有荷载。按查表求内力的方法，分别计算各种活载布置情况下的内力，并绘图：

图3.24（a）为恒载作用下的内力图；图（b）为两跨有活载时的内力图；图（c）为左跨有活载时的内力图；图（d）为右跨有活载时的内力图；图（e）为（a）+（b）、（a）+（c）、（a）+（d）三种情况下的内力叠合图，其外包线即为内力包络图。

5.支座截面内力的计算

弹性理论计算时，无论是梁或板，按计算简图求得的支座截面内力为支座中心线处的最大内力，但此处的截面高度却由于与其整体连接的支承梁（或柱）的存在而明显增大，故其内力虽为最大，但并非最危险截面。因此，可取支座边缘截面作为计算控制截面，其弯矩和剪力的计算值，近似地按下式求得（图3.25）

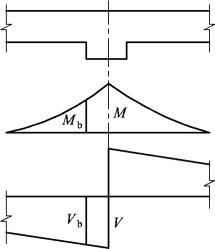
图3.25　支座处弯矩、剪力图

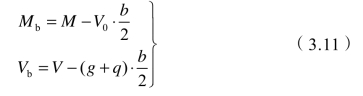
式中：M、V为支座中心线处截面的弯矩和剪力；V0为按简

支梁计算的支座剪力；g、q为均布恒载和活荷载；b为支座宽度。