风荷载是指风遇到建筑物时在其表面产生的一种压力或吸力。风荷载与风压、建筑物表面形状及建筑物的动力特性有关,设计主体结构时,垂直于建筑物表面上的风荷载标准值按下式计算:
![]()
式中 w0——基本风压(kN/m2);
βz——高度z处的风振系数;
μz——风压高度变化系数;
μs——风荷载体型系数。
风荷载的组合值系数、频遇值系数和准永久值系数可分别取0.6、0.4和0。
1.基本风压w0
基本风压是根据空旷平坦地面上离地面10m高统计所得50年一遇的10min平均最大风速v0,按w0=ρv02/2(ρ为空气密度)换算而来的。在结构设计时,其取值不得小于0.3kN/m2。对于高层建筑、高耸结构以及对风荷载比较敏感的其他结构,基本风压的取值应适当提高,并应符合有关结构设计规范的规定。
当考虑重现期不同于设计规范规定的50年时,应将荷载规范50年一遇基本风压值乘以相应的修正系数μ,见表2.13。
表2.13 不同重现期基本风压修正系数μ

2.风压高度变化系数μz
由于空气本身具有一定的黏性,能承受一定的切应力,因此在与物体接触表面附近形成一个具有速度梯度的边界层气流,导致风速随高度和地貌情况而变化。基本风压是建立在平坦地面上空10m高度处的风速基础之上的,对于不同高度及地貌情况,需要对风压进行修正,用风压高度变化系数来反映,见表2.14。
表2.14 风压高度变化系数μz
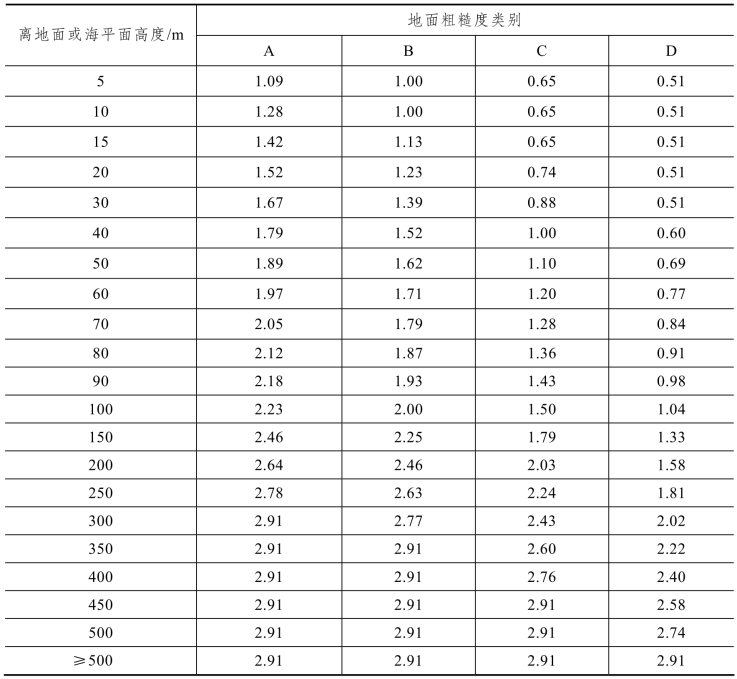
地貌方面,《建筑结构荷载规范》(GB 50009—2010)将地面粗糙度类别分为4类:A类指近海海面和海岛、海岸、湖岸及沙漠地区;B类指田野、乡村、丛林、丘陵以及房屋比较稀疏的乡镇;C类指有密集建筑群的城市市区;D类指有密集建筑群且房屋较高的城市市区。
对于山区建筑和远海海面及海岛上的建筑,还需考虑地形条件的修正,修正系数详见《建筑结构荷载规范》(GB 50009—2012)。
3.风荷载体型系数μs
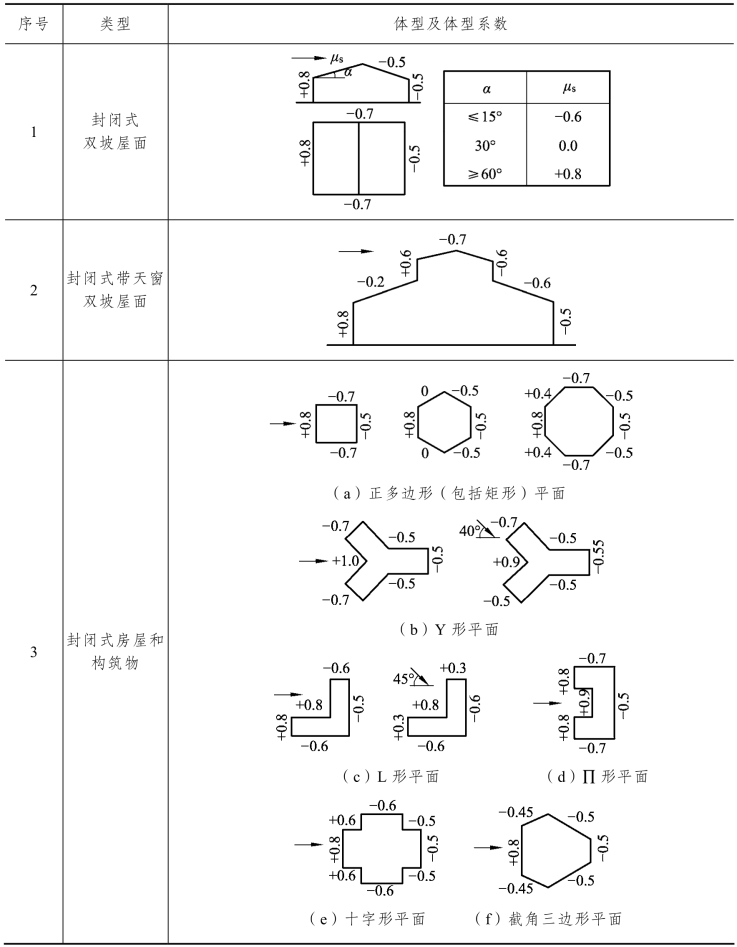
由风速换算得到的风压是所谓来流风的速度压,并不能直接作为建筑物设计的结构荷载,因为房屋本身并不是理想地使原来的自由气体停滞,而让气流以不同方式在房屋表面绕过,房屋会对气体形成某种干扰。完全用空气动力学原理分析不同外形建筑物表面风压的变化,目前还存在困难,一般根据风洞试验来确定风载体型系数。表2.15是部分建筑物的风载体型系数,正值表示压力,负值表示吸力。
表2.15 部分建筑物的风荷载体型系数μs
4.风振系数βz
风压的变化可以分为两部分:一是长周期部分,其周期从几十分钟到几小时;二是短周期部分,常常只有几秒钟。为便于分析,可以把实际风分解为平均风分量和脉动风分量。平均风的周期比一般结构的自振周期大得多,因而对结构的响应相当于静力作用;而高频的脉动风周期与高层和高耸结构的自振周期相当。因此,《建筑结构荷载规范》(GB 50009—2012)规定,对于高度大于30m且高宽比大于1.5的房屋,以及自振周期大于1.5的高耸结构,应考虑脉动风压对结构产生顺风向风振的影响。
对于一般竖向悬臂型结构,例如高层建筑和构架、塔架、烟囱等高耸结构,均可仅考虑结构第一振型的影响,高度z处的风振系数βz可按下式计算:
![]()
式中 g——峰值因子,可取2.5;
I10——10m高度名义湍流度,对应A、B、C和D类地面粗糙度,可分别取0.12、0.14、0.23和0.39;
Bz——脉动风荷载的背景分量因子;
R——脉动风荷载的共振分量因子。
(1)脉动风荷载的共振分量因子R可按下列公式计算:

式中 f1——结构第1阶自振频率(Hz),第1阶自振周期对钢结构可近似取T1=(0.1~0.15)n,混凝土框架结构T1=(0.08~0.10)n,混凝土框架-剪力墙和框架-筒体结构T1=(0.06~0.08)n,剪力墙和筒中筒结构T1=(0.05~0.06)n,n为层数;
kw——地面粗糙度修正系数,对A类、B类、C类和D类地面粗糙度分别取1.28、1.0、0.54和0.26;
ζ1——结构阻尼比,对钢结构可取0.01,对有填充墙的钢结构房屋可取0.02,对钢筋混凝土及砌体结构可取0.05,对其他结构可根据工程经验确定。
(2)脉动风荷载的背景分量因子Bz可按下式计算:

式中 φ1(z)——结构第1阶振型系数;
H——结构总高度(m),对A、B、C和D类地面粗糙度,H的取值分别不应大于300m、350m、450m和550m;
ρx——脉动风荷载水平方向相关系数;
ρz——脉动风荷载竖直方向相关系数;
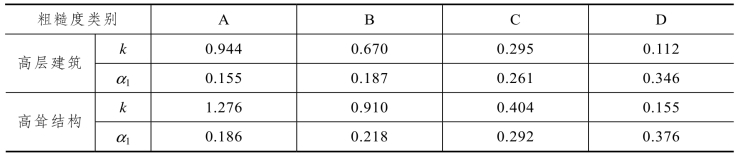
k,α1——系数,按表2.16取值。(https://www.xing528.com)
表2.16 系数k和α1
①水平方向相关系数ρx可按下式计算:

式中 B——结构迎风面宽度(m),B≤2H。
②竖直方向相关系数ρz可按下式计算:

式中 H——结构总高度(m),对A、B、C和D类地面粗糙度,H的取值分别不应大于300m、350m、450m和550m。
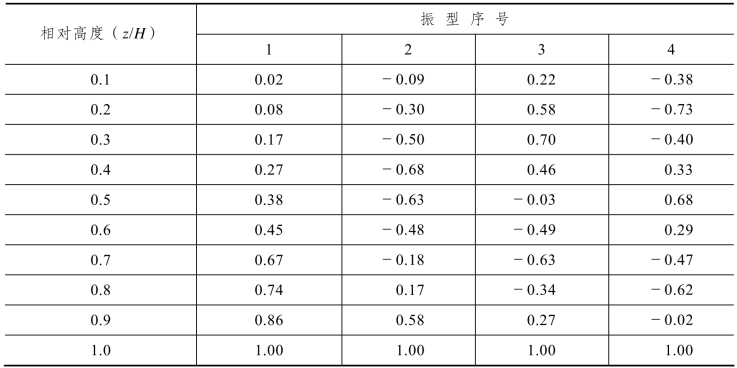
③振型系数φ1(z)应根据结构动力计算确定。对外形、质量、刚度沿高度按连续规律变化的竖向悬臂型高耸结构及沿高度比较均匀的高层建筑,振型系数也可根据相对高度z/H按《建筑结构荷载规范》(GB 50009—2012)附录G确定。表2.17为高层建筑的振型系数。
表2.17 高层建筑的振型系数φ1(z)
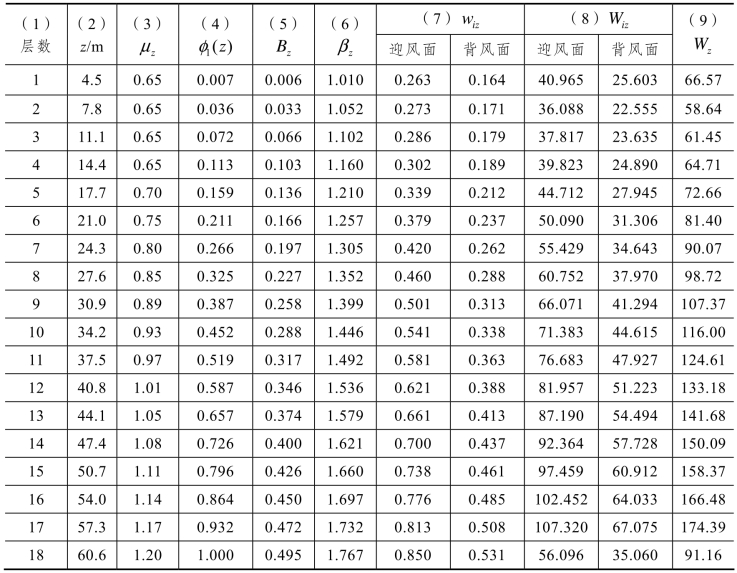
【例2.1】 已知正方形平面钢筋混凝土框架-剪力墙结构高层建筑,平面边长40m,如图2.5所示。该建筑共18层,底层层高4.5m,其余层高均为3.3m,平面沿高度保持不变,质量和刚度沿竖向均匀分布。地面粗糙度为C类,所在地区的基本风压w0=0.5kN/m2。试计算各楼层处顺风向总的荷载标准值。
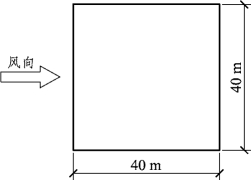
图2.5 房屋的平面形状

图2.6 风荷载体型系数
【解】(1)确定风荷载体型系数μs。
查表2.15,迎风面的体型系数为+0.8,为压力,背风面的体型系数为-0.5,为吸力(图2.6)。
(2)计算各层的风压高度变化系数μz。
近似假定室内外地面标高相同,各层楼面离室外地面的高度z列于表2.18第2列,查表2.14或根据《建筑结构荷载规范》(GB 50009—2012)提供的风压高度变化系数计算公式可算得各层楼面标高处的风压高度系数μz,列于表2.18第3列。
(3)计算风振系数βz。
混凝土框架-剪力墙结构第1阶自振周期近似取T1=0.07n=1.26s,f1=1/T1=0.794Hz;C类地面粗糙度修正系数kw=0.54;钢筋混凝土结构的阻尼比ζ1取0.05。由式(2.14),有

各楼层位置第1阶振型系数φ1(z)按表2.17计算,列于表2.18第4列。
房屋的总高度H=60.6m,迎风面宽度B=40m,由式(2.16)、(2.17)可求得水平方向相关系数和竖直方向相关系数。
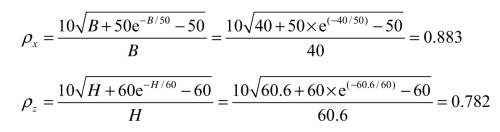
由表2.16,C类地面粗糙度的高层建筑,可得k=0.295,α1=0.261,由式(2.15)可得背景分量因子
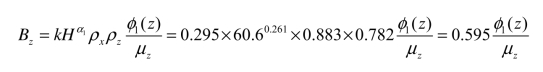
由式(2.13)可得风振系数
![]()
(4)计算迎风面和背风面不同高度处的分布荷载。
wiz=βzμzμsw0
计算结果列于表2.18第7列。
(5)计算各楼面处的集中荷载。
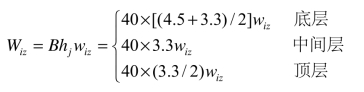
式中:B为迎风面或背风面宽度;hj为j层楼面上、下层层高的平均高度。
(6)计算各楼层处总的集中荷载。
Wz=Wyz+Wbz
计算结果详见表2.18最后一列。
表2.18 风荷载计算结果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




