【摘要】:结构能够完成预定功能的概率称为可靠概率Ps,不能完成预定功能的概率称为失效概率Pf。当仅有结构抗力R和作用效应S两个基本变量且相互独立时,失效概率Pf可以表达为:由上式可以看出,即使最简单的情况,也需要对这两个变量的概率密度函数进行积分运算,而且并不是对所有的情况都能得到解析解。
结构能够完成预定功能的概率称为可靠概率Ps,不能完成预定功能的概率称为失效概率Pf。结构的可靠性可用可靠概率Ps来度量,也可用失效概率Pf来度量。
当仅有结构抗力R和作用效应S两个基本变量且相互独立时,失效概率Pf可以表达为:

由上式可以看出,即使最简单的情况,也需要对这两个变量的概率密度函数进行积分运算,而且并不是对所有的情况都能得到解析解。对于多个随机变量,计算失效概率则需要进行多重积分,当各变量间相关时,还需要知道它们的联合概率分布函数并进行积分运算。
因此,虽然用失效概率Pf来度量结构的可靠性物理意义明确,也已为国际上所公认。但是计算Pf非常复杂,很难直接按上述方法来度量结构的可靠性。
当仅有结构抗力R和作用效应S两个基本变量且均按正态分布时,结构的功能函数Z=R-S也服从正态分布,且其均值和标准差分别为:(https://www.xing528.com)

这种情况下,计算失效概率Pf可大为简化。图2.4所示为结构的功能函数Z=R-S的概率密度函数,结构的失效概率Pf可直接通过Z<0的概率来表达(图中阴影部分面积),将两个基本变量的正态分布标准化后,失效概率可以表达为:

式中 Φ(·)——标准正态分布函数。
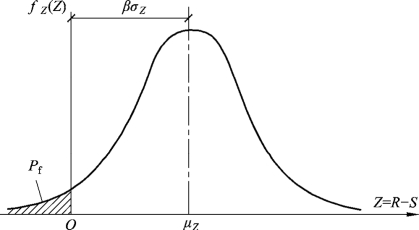
图2.4 失效概率Pf与可靠指标β的关系
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




