拱的受力特点优化为：拱形结构的受力特点分析

为说明拱式结构的基本受力特点，下面以较简单的三铰拱为例进行拱的受力分析，并与同跨度受同样荷载作用下的简支梁进行比较。

1.支座反力

设三铰拱受竖向荷载作用如图1.25所示。以整个结构为脱离体，在支座处分别代之以支座反力VA、VB、HA和HB，由平衡方程的分析可以得到拱结构的竖向反力VA、VB，与相同跨度、承受相同荷载简支梁所产生的竖向反力相同。

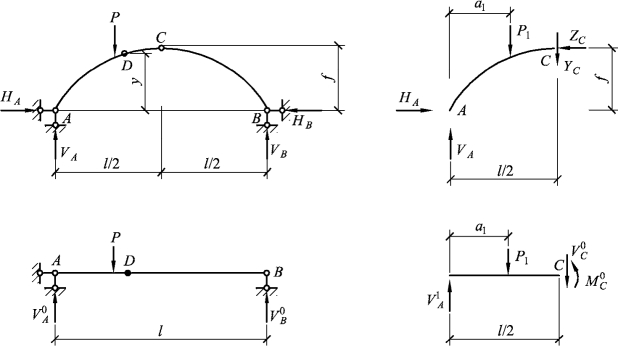
图1.25　三铰拱的受力分析

拱结构的水平推力为：

式中：为简支梁在C截面处的弯矩；f为拱的矢高。

通过上面的例子可知：

（1）在竖向荷载作用下，拱脚支座内将产生水平推力。拱脚水平推力的大小等于相同跨度简支梁在相同竖向荷载作用下所产生的在相应于顶铰C截面上的弯矩除以拱的矢高f。

（2）当结构跨度与荷载条件一定时（为定值），拱脚水平推力（HA＝HB）与拱的矢高f成反比。

2.拱身截面的内力

为求拱身D截面处的内力，取脱离体如图1.26所示。从结构力学中我们知道，拱杆任意截面的内力为：

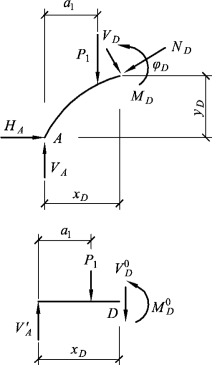
图1.26　拱身内力计算图(https://www.xing528.com)

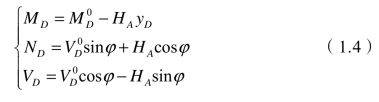
式中：与为相应简支梁的弯矩和剪力。

由式（1.4）可知：①拱身内的弯矩小于相同跨度、相同荷载作用下简支梁内的弯矩；②拱身截面内的剪力小于相同跨度、相同荷载作用下简支梁内的剪力；③拱身截面内存在有较大的轴力，而简支梁中是没有轴力的。

3.拱的合理轴线

前面已经提到，轴心受力构件截面上应力分布均匀，可以充分利用材料的强度。因此，拱式结构受力最理想的情况应是使拱身内弯矩为零，仅承受轴力。对于三铰拱结构由式（1.4）可知，当=0时，则

由（1.5）可知，只要拱轴线的竖向坐标与相同跨度、相同荷载作用下的简支梁弯矩值成比例，即可使拱截面内仅有轴力没有弯矩。满足这一条件的拱轴线称为合理拱轴线。在沿水平方向均布的竖向荷载作用下，简支梁的弯矩图为一抛物线，因此，在竖向均布荷载作用下，合理拱轴线应为一抛物线。对于不同的支座约束条件或荷载形式，其合理拱轴线的形式是不同的。例如，对于受径向均布压力作用的无铰拱或三铰拱，其合理拱轴线为圆弧线。见图1.27。

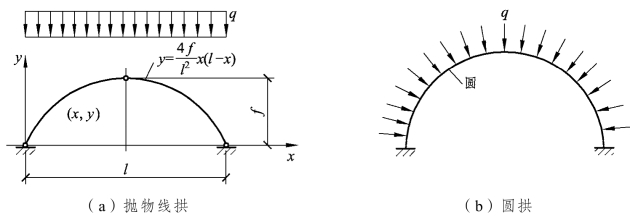
图1.27　拱的合理轴线

4.拱的矢高

不同的建筑对拱的形式要求不同，有的要求扁平，矢高小，有的则要求矢高大。合理拱轴的曲线方程确定之后，可以根据建筑的外形要求定出拱轴的矢高。以三铰拱为例，在沿水平方向均布的竖向荷载作用下，拱的合理轴线为二次抛物线，当矢高f不同时，拱轴形状也不相同，如图1.28所示。

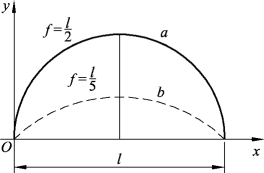
图1.28　拱的合理轴线与矢高

由此可见，矢高对拱的外形影响很大。它直接影响建筑造型和构造处理。矢高还影响拱身轴力和拱脚推力的大小。水平推力H与矢高f成反比。因此，设计时确定矢高大小，不仅要考虑建筑外形要求，还要考虑结构的合理性。