NVH制动盘的不同应用介绍

图5-78 制动盘的不同应用

a）三维实体模型 b）线框模型

计算模态根据结构的几何形状、边界条件和材料属性，将结构的质量分布、刚度分布和阻尼分布分别用质量矩阵、刚度矩阵和阻尼矩阵表示出来，如上一小节的基本运动方程所示，通过质量矩阵、刚度矩阵和阻尼矩阵确定结构的模态参数。计算模态不考虑方程中的外力向量，主要是对方程进行特征值求解，首先获得特征值，然后获得特征向量。而特征值就是模态频率，特征向量就是模态振型。

特征值求解的数学处理可采用一些不同的方法实现。这些方法又分为直接求解和间接求解。对于规模较小的矩阵，采用直接求解方法分解方程组，得到所有的特征值和特征向量。常用的直接求解方法有雅可比（Jacobi）、吉文斯（Givens）和豪斯霍尔德（Householder）等。当矩阵的规模更大时，如大型有限元模型常使用一些间接方法，但这些间接方法只能得到一些低阶模态（高阶模态难以收敛）。这些间接方法如子空间迭代法（Subspace Iteration）、同步向量迭代法（Simultaneous Vector Iteration）和兰索斯方法（Lanczos）等。

在此不关注这些方法的细节，只讨论特征值求解和在何时能得到频率和模态振型。因此，一般形式的特征值求解方程如下：

（K-λ[M]）x=0

首先，特征值可从矩阵的行列式中得到。这个行列式其实就是一个高阶多项式，多项式的根也就是特征值（模态频率）。这些根数值上可通过任何根求解算法获得，这些算法如正切方法（SecantMethod）、牛顿-辛普森方法（Newton-Rapson Method）等。

因此，特征方程和一个可能的典型多项式，如图5-79所示。函数过零位置就是多项式等于零时的根。

（K-λM）x=0

既然已经给出了方程组的频率，那么下一步就是确定模态振型。如果你使用第一个特征值，λ=ω²₁，代入到特征方程，那么就能求解得到向量x₁，因为M、K和ω²₁是已知的。求解这个向量可直接使用一些分解模式，如克劳特-杜利特尔（Crout-Doolittle）分解法、乔里斯基（Cholesky）分解法、LDL分解法等。

向量x₁实际上就是那个特定频率对应的模态振型，而正是使用这个频率去求解方程组，得到与这个频率相对应的向量。图5-80所示为自由梁的第1阶自由-自由弹性模态，注意使用特征值λ₁去确定系统的第1阶模态。如果进一步求解如图5-80所示方程，将会发现弹性力等于惯性力。我们可以说这根梁在频率ω²₁处处于动态平衡状态。如果从能量角度去观察这个系统，你将会明白为什么会存在节点，系统将围绕这些节点振荡，在这些节点处系统的振型有相等的正负部分，使得系统处于平衡状态。

图5-79 行列式的根的图形表示(www.xing528.com)

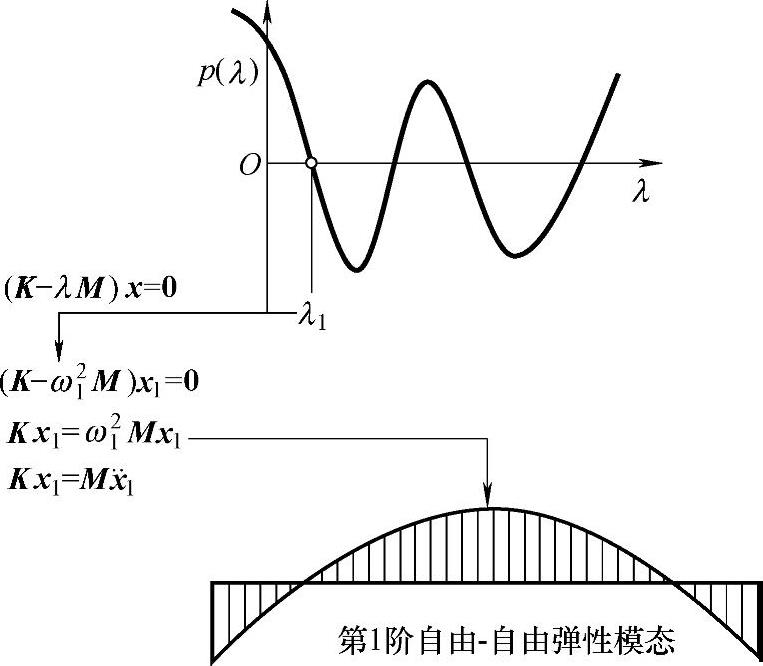
图5-80 第1阶模态的特征值求解示意

当然，我们可以为第2阶频率做相同的事情，然后继续求解所有感兴趣的模态。笔者讲解的过程可能会采用不同的求解算法去分解这个矩阵，以获得最终的答案。目的是使你更明白整个过程，即计算模态从基本运动方程中怎样求解频率和模态振型。

因此，重要的是要知道计算模态的特征值求解是获得所谓的特征对，也就是与特征方程相关的频率和向量，这个向量就是模态振型。另一件要知道的事是模态振型之间是线性无关的，同时关于质量和刚度矩阵是正交的。这是特征值求解带来的副产品。

试验模态是通过数据采集设备测量结构上一些位置的输入输出，然后将时域数据转换到频域，得到频响函数，再由模态参数估计算法估算结构的模态参数。试验方法仅仅测量结构的输入和输出，由输入输出计算频响函数FRF，不测量结构的质量和刚度。

频响函数FRF元素的分子为留数，留数与模态振型直接相关。分母包含系统极点信息，也就是系统的频率和阻尼信息。因此，从频响函数矩阵可以得到系统全部的模态信息。频响函数如下（下标r表示阶数）：

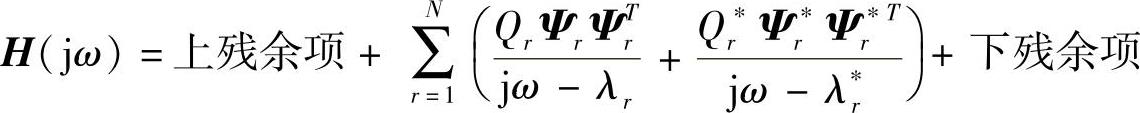
这个方程感兴趣的部分是留数和极点，虽然留数的改变依赖于特定的输入-输出组合，但是极点保持不变。这暗示着系统极点是全局特性，它们独立于特定的输入-输出位置。也就是说从一个输入-输出位置就能测量到系统的所有极点（频率和阻尼）信息。因此，固有频率测量，理论上讲，只需要一个测量位置即可测量出所有的模态频率（实际测量时要避开节点位置）。

然而，留数却依赖于特定的输入-输出位置，随输入-输出位置的变化而变化。也就是说不同输入-输出位置的留数是不相同的，这就说明了为什么测量模态振型时，需要大量的测点。这是因为不同测点的留数是不同的，留数是局部特征，留数不同也就是振型值不同，因此，振型依赖于不同的测量位置，为了将振型唯一地描述出来，要求测点数目尽量多，通过这些测点位置的振型值能唯一地表征这些模态振型。

现今多数模态参数估计方法，通常分两个处理步骤。首先估计极点，然后计算留数或模态振型（要求先提取到整体极点）。记住这一点：进行系统极点估计时，不需要使用所有的FRF，可以使用部分频响函数，也就是那些最能合理描述感兴趣的极点的频响函数来估计系统极点。一旦得到系统整体极点，那么留数或者模态振型就可以使用所有测量DOF的FRF提取到。

有一种算法叫作峰值拾取法，就是利用FRF的虚部，它同时表明了幅值和响应的方向，其中方向是最重要的信息。将各个测点位置的各阶FRF虚部峰值连接起来，就是相应的模态振型。当然这是早期的方法，现今已不再使用。

因此，从理论角度上讲，计算模态采用的方法是对基本特征方程进行特征值求解，获得特征值与特征向量，也就是模态频率和振型。而试验模态则测量输入输出计算频响函数，采用曲线拟合的方式获得模态频率和振型。因此，二者从方法论上来讲，有着本质的区别。