曲线拟合的定义与应用

在进一步讲解曲线拟合之前，我们需要明白两个事情。

第一，实测获得的FRF是离散的，不是连续的，可能初看起来，类似图5-54所示的FRF曲线是连续的，但实际上是离散的，是由若干条谱线所组成的，而每条谱线对应一个数据点，所以FRF实质上是由若干个离散的数据点组成的，而曲线拟合就是对这些离散的数据点进行拟合，得到一条新的由各阶模态参数表征的曲线，也就是综合的FRF曲线。这就是为什么模态参数提取的过程称为曲线拟合的原因所在。

第二，我们常说模态参数是这三个参数：频率、阻尼和振型，而极点包含频率和阻尼信息，留数与振型直接相关，因此，曲线拟合实际上是得到每阶模态的极点和留数信息。如果在测量的频带内有n阶模态，而每阶模态都有这两个参数（极点和留数），总共有2n个模态参数需要提取。那么曲线拟合就是为了提到到这2n个模态参数。

为了理解曲线拟合，先考虑一下最简单的直线拟合和二次抛物线拟合。

考虑用一根直线拟合一些测量数据。我打算用最小二乘误差最小的方法为图5-57所示的数据进行拟合。当然，使用的数学模型为

y=kx+b

这有两个参数定义这条直线，也就是斜率k和Y方向的截距b。通过曲线拟合是为了获得这两个参数。同时认识到这两个参数是由一组测量数据得到的，而这些测量数据存在一些变动，如图5-57所示，如果选择不同的两组数据：一组两个点（曲线1）与另一组两个点（曲线2），两组数据计算出来的斜率和Y方向的截距显著不同。换句话说，斜率和Y方向的截距都有差异，数据不一致，这依赖于提取参数所使用的数据。而使用最小二乘拟合所有的数据则是斜率和Y方向截距的“最优”估计。

同理，让我们考虑一下二次抛物线，它的方程为

y=ax²+bx+c

确定这条曲线需要确定三个参数a、b和c。当对数据点进行拟合时，就是为了确定这三个参数。同直线拟合一样，使用不同的测量数据进行拟合时，得到的这三个参数是有差异的，这时为了将差异最小化，也需要使用最小二乘估计以获得这三个参数的最优估计。在这还有一点需要强调一下，当使用的曲线幂次越高时，需要确定的参数也就越多，从二次抛物线和直线拟合可以看出，二次抛物线需要确定的参数比直线拟合多了一个。

实际上，模态参数提取所用的曲线拟合跟上面的直线或抛物线拟合原理是类似的，只不过比上面要复杂些。结构的模态可以通过下面的频域表达式来描述：(www.xing528.com)

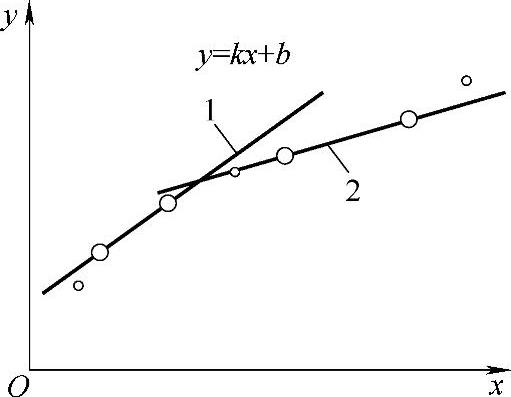
图5-57 测量数据带来的影响

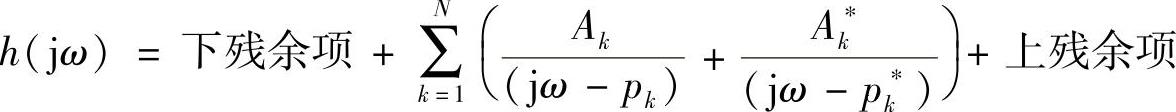
从上式可以看出，模态的曲线拟合是用复数，而不是实数。

与之前的直线或抛物线拟合相比，FRF曲线比它们更复杂，数据点更多。单个FRF有多少条谱线就有多少个数据点，有多少个测量自由度，就存在多少条这样的FRF曲线，如果同时有两个或两个以上的激励点，还需要乘以激励点数，这样，实际用于拟合的数据点是非常庞大的。

与抛物线相比，模态的曲线拟合不是使用更高幂次项曲线，而是使用上面方程中括号里的多项式。那是不是表明，假如在分析带宽内只有10阶模态，就只用这10阶模态所对应的多项式来进行曲线拟合呢？当然要包括这10阶所对应的多项式，但同时也要包含更多的残余项，这样拟合得到的结果才会更精确。而具体使用多少阶参与拟合，这就由Modal size这个参数来决定。

与直线或抛物线拟合相比，模态的曲线拟合得到的参数更多，具体参数的多少视分析带宽内的模态阶数而定。每阶模态需要确定两个参数：极点和留数，因此，需要确定的参数是模态阶数的2倍。

模态中的曲线拟合，除了数据是复数、曲线更复杂和需要确定的参数更多外，实际跟直线拟合相同。原理上跟直线拟合是相同的方法论。我们在离散数据点测量到的数据是复数形式，将这些数据拟合成频响函数曲线，目的是用最小二乘估计找到描述这组数据最合适的参数。

因此，如果你理解了这个直线拟合流程，那么你不得不同意在模态参数估计过程中应用相同的流程（当然了，模态拟合中这些数都是复数形式，且曲线更复杂，参数更多）。模态参数估计仅仅是简单的直线拟合的延伸。