从计算模态的角度来讲,由特征值求解得到的特征值和特征向量分别对应一阶模态频率和模态向量(当然也可能存在重根)。模态振型也称为模态向量、模态振型向量、模态位移向量。模态振型是结构节点(注意不是模态中的节点)或测点的函数,如有限元模型节点数上万,甚至上百万,模态振型就是这些节点的函数。而在试验模态中,由于测点数量远小于有限元模型的节点数,通常测点数从数个到数百个,因此,试验模态振型就是这些测点的位置函数。由于结构有无限多阶模态,因此每一阶模态振型都不相同,也就是模态振型除了是结构位置的函数之外,还是模态阶数的函数。
对计算模态而言,由于节点数成千上万,因此,对于描述每一阶模态振型来说,这些节点数量总是足够的。但对于试验模态而言,为了合理地描述模态振型,要求测量自由度必须足够,不然不仅不能唯一地描述所关心的模态振型,而且还可能存在空间上的混叠。
模态振型,通俗地讲是每阶模态振动的形态。但从数学上讲,模态振型是模态空间的基向量。在线性代数中,基向量是描述、刻画向量空间的基本工具。向量空间中任意一个元素,都可以唯一地表示成基向量的线性组合。在模态空间,这个基向量的个数就是模态的阶数。
在进一步介绍模态振型之前,先让我们介绍回顾一下二维空间上的一些特征。在二维空间,也就是直角坐标系中,相应的基向量是(1,0)和(0,1)。二维空间,如图5-47所示,空间上任一坐标都可以用这两个基向量来表示(当然这个相当简单)。
图5-47 二维空间
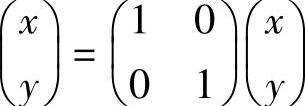
而在模态空间中,对应的为模态向量与模态坐标,模态向量就是模态振型,是模态空间中的基向量。而模态坐标是加权系数,是各阶模态对响应的贡献量。因此,对于线性时不变系统而言,系统任一点i的响应均可表示为各阶模态振型值与模态坐标q的乘积,即各阶模态在这个位置产生的响应的线性叠加:

式中,φir为第i个测点的第r阶模态振型值,N表示模态阶数。由M个测点的振型值所组成的列向量,就是第r阶模态向量:
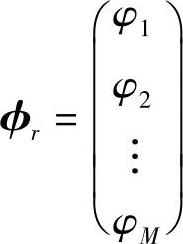
它反映的是该阶模态的振动形状,即这阶模态振型。由各阶模态向量组成的矩阵称为模态矩阵,记为
Φ=(ϕ1,ϕ2,…,ϕN)(https://www.xing528.com)
它是一个M×N的矩阵。将各阶模态坐标记为
Q=(q1(ω),q2(ω),…,qN(ω))T
因此,各个测点的响应为

可以简记为
X(ω)=ΦQ
通过上式,我们可以明白,结构任何一点的响应都可以用模态向量与模态坐标的乘积来表示,这也验证了模态分析实质上是一种坐标变换方式。从这也可以验证普通的振动测试是模态的表象,实质起作用的还是模态。或者可以说,通常我们测试的响应是处于某种运动状态下的结构被激起来的那些模态在测量位置处响应的叠加。
由于频响函数为复数,得到的模态振型值也为复数。因此,可以用幅值与相位或实部与虚部来表示模态振型值。在这,给出一个自由-自由梁第1阶弹性模态振型实例。对一根自由-自由梁划分15个测点,通过试验模态分析得到的第1阶模态振型如图5-46所示,这15个测点的模态振型值见表5-4。另一方面,虽然振型值有实部与虚部,但振型动画用的是幅值与相位来显示。幅值表示运动幅度,而相位则表示运动方向。
表5-4 梁的第1阶弹性模态振型

(续)

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




