单自由度系统在模态中的响应

从计算角度上讲，模态分析是将物理空间上复杂的、耦合的运动方程通过特征值求解和模态变换方程变换到模态空间，在模态空间这组物理空间上耦合的方程变成了一组解耦的单自由度系统的运动方程，如图5-44所示。模态空间使得我们更易于用单自由度系统去描述结构系统。

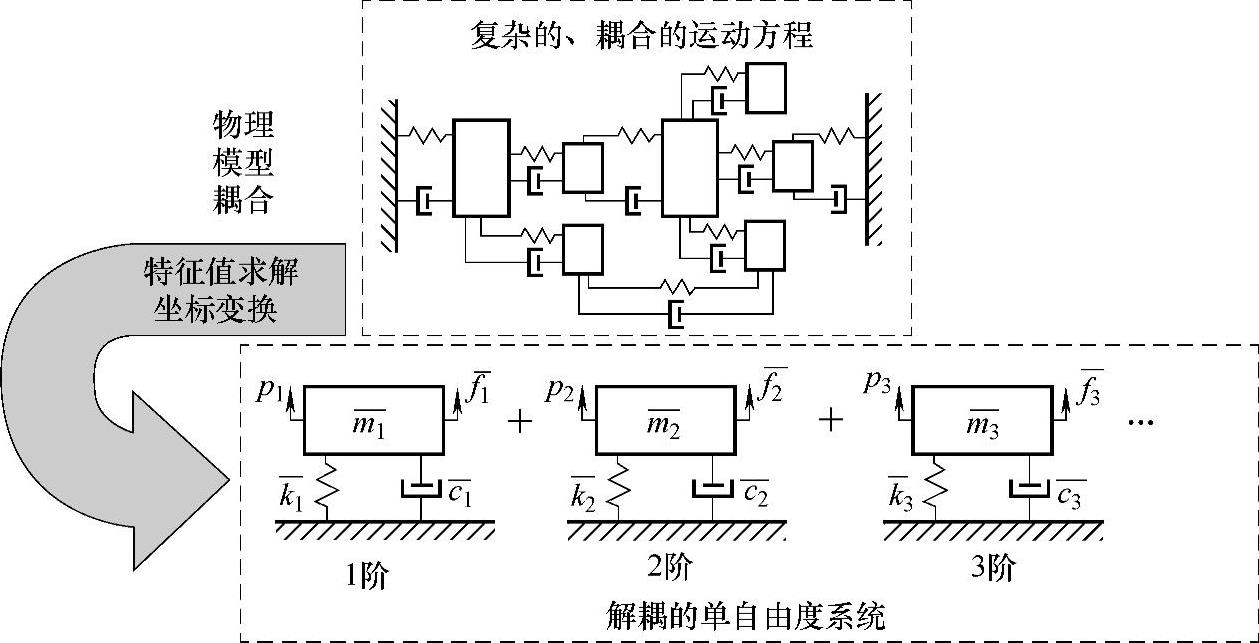
图5-44 模态坐标变换

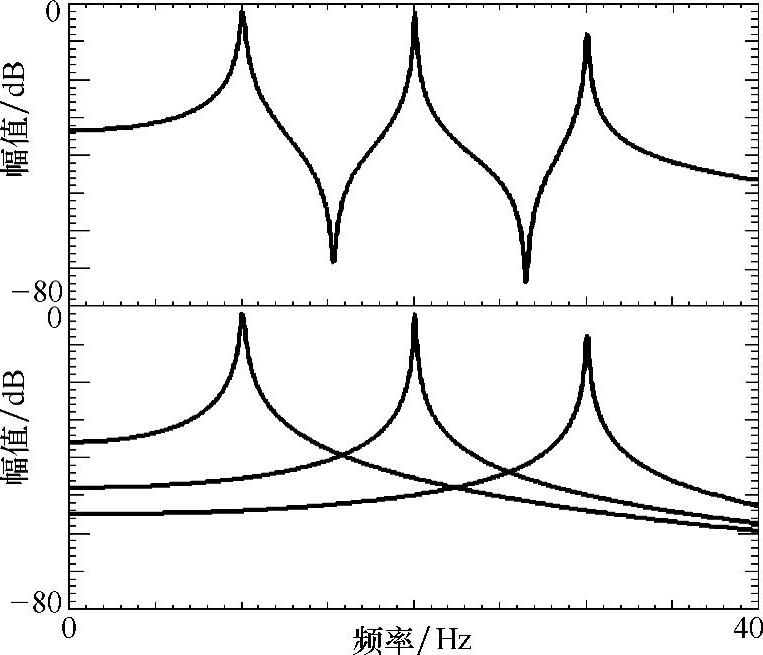
从试验模态分析角度上讲，通过对测量的频响函数进行曲线拟合，提取到各阶模态参数，每阶模态都是单自由度系统，如图5-45所示，试验模态分析将图5-45中上侧的FRF曲线分解成下侧的三个单自由系统。

通过4.1什么是固有频率一节，我们已经明白，1个自由度对应1阶模态（包括频率、阻尼和振型）。如图5-46所示为自由-自由梁的第1阶弹性模态，测量自由度为15，也就是说由这15个测量自由度绘得第1阶的模态振型（见图5-46）。这阶模态是一个单自由度系统，但是在这个振型中却有15个测量自由度，而不是1个测量自由度，那模态中的单自由度与我们平常所说的自由度相同吗？一个测点一个方向是一个自由度，在这个梁中它有15个测点，每个测点仅测量一个方向，因此，它有15个测量自由度。

(www.xing528.com)

图5-45 试验模态分析中的三阶模态

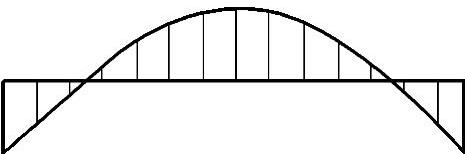
图5-46 自由-自由梁第1阶模态振型

首先，让我们回顾一下自由度的定义。自由度是确定系统在空间上运动所需要的最少、独立的坐标系的个数。在这个梁结构中，一个测点是一个自由度，共有15个自由度，但是在这阶模态振型中，只要确定其中任何一个测点的振型值（也称振型系数），那么其他测点的振型值也就确定了（包括方向），也就是说每个测点之间都存在特定的关系，而这种特定的关系就是由这阶模态振型所决定的，因此，只需要使用一个自由度就可以确定这阶模态的振型，所以，一阶模态称之为一个单自由度系统。因而，模态中的单自由度系统与我们平常所说的单自由度是相同的。一阶模态称为一个单自由度系统，这时与测点数量没有关系，因为每个测点之间都有固定的关系，这个关系就是由模态振型决定的。