传递函数、频响函数和传递率的区别解析

首先，让我们以部分分式的形式写出单自由系统的传递函数，形如

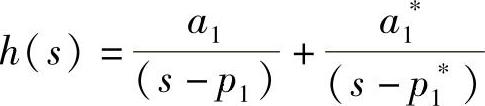
对于小阻尼系统的传递函数的根或者极点可以写为

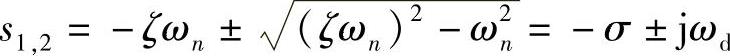
因为传递函数是复值函数，所以函数的根将是两个变量σ和ω的函数，这两个变量分别为这个根的实部和虚部。分子称为系统传递函数的留数（命名为留数是因为它来自于留数定理，用它来估计这个函数）。注意到这两个根为复数，因此传递函数的自变量取值为整个复平面。

现在我们绘出这个函数所对应的曲线图，该图将映射成一个曲面，因为该函数是通过两个独立变量σ和ω定义的。因此，如果我们保持σ为不变，ω变化，然后逐渐改变σ，重新计算ω的范围，这时将产生一个复数值矩阵。因为这些数值是复数，我们可以分别绘出它们的实部和虚部图，当然也可以绘出函数的幅值和相位图。无论如何，可以用这些形式中的任何一个来绘制这个曲面，用于描述系统的传递函数。这些图如图5-20所示。我们可以讨论系统传递函数的每一个子项（实部和虚部，幅值和相位），但在此只想关注传递函数的幅值。

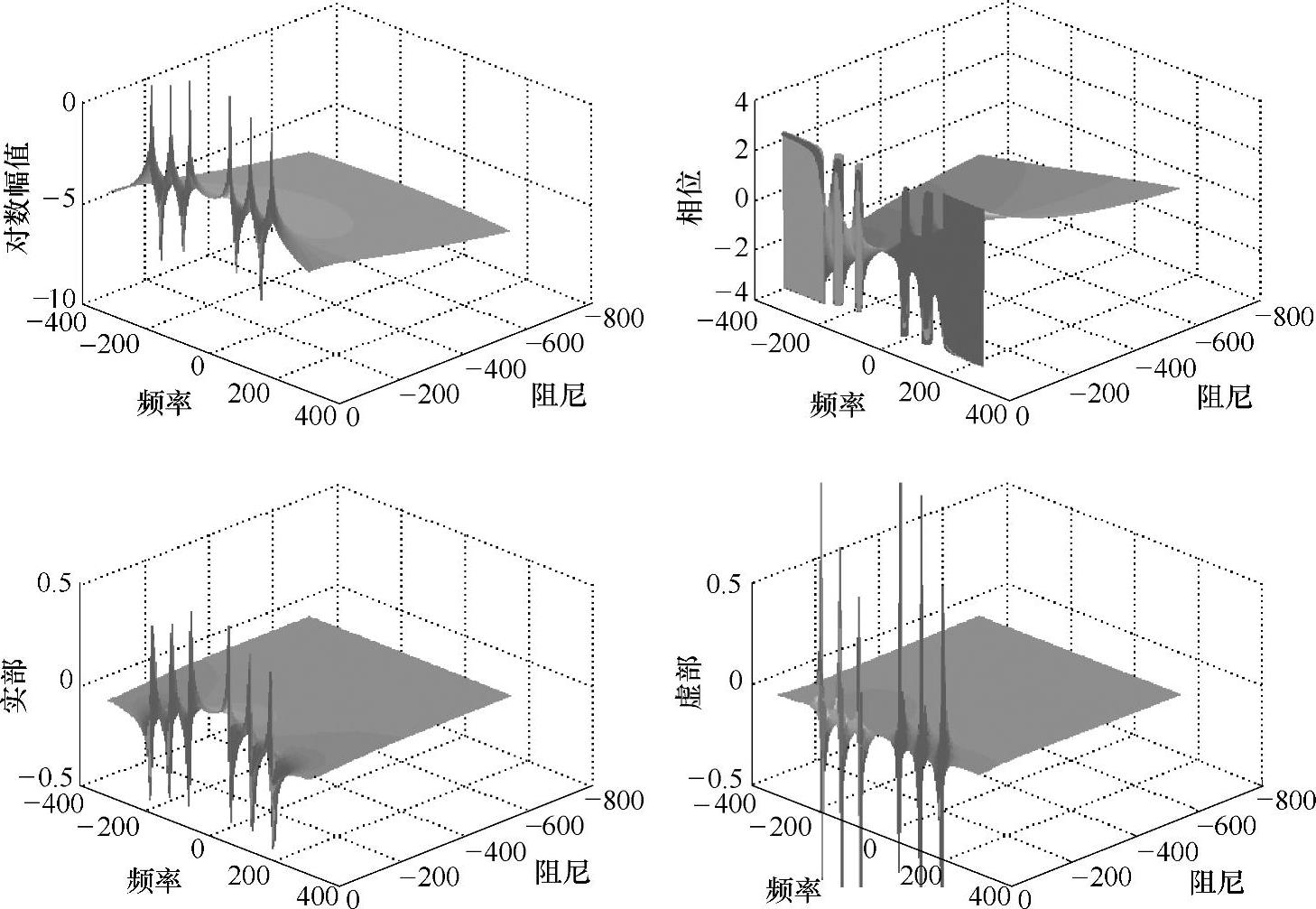
图5-20 系统传递函数

如果我们考虑系统传递函数的切片——频响函数，那么在σ=0时估计这个函数，也就是说传递函数沿频率jω轴估计。我们可以写出频响函数，形如

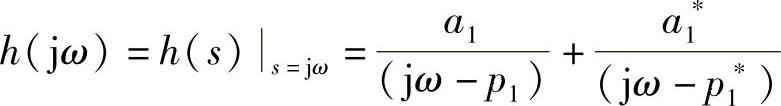
如果我们对比传递函数和频响函数的表达式，会发现在传递函数中独立变量是s，而频响函数中独立的变量是ω，函数h的值依赖于这些变量。但是，同时也注意到频响函数另外两个参数为留数a和极点p。因此，由这两个参数定义在给定ω区间下的频响函数h值，我们称这些参数为模态参数。

如果我们考虑系统传递函数沿jω轴估计的幅值，并且将其投影到沿jω轴的切片平面上，那么我们将看到如图5-21所示的投影切片（黑色曲线）。而这正好是我们用FFT分析仪测量得到的曲线：频响函数。并且我们可以看出，这只有一个独立变量ω用于描述频响函数。同时，我们也注意到我们仅用一条曲线，而不是一个曲面来描述系统的频响函数。

我们已经明白了频响函数由何而来，因此我们说频响函数是传递函数的子集，是传递函数沿频率轴的估计。传递函数的自变量是整个复平面，也就是拉普拉斯域，而频响函数的自变量仅是沿虚轴，也就是沿频率轴变化，对应的是傅里叶域。这些域之间有什么关系呢？

通常我们在时域测量信号（振动噪声发生的事件）或表征基本运动方程，时域信号通过傅里叶变换到频域（傅里叶域），频域通过傅里叶逆变换到时域。频域仅仅是随频率变化，是从实数的角度来考虑的。而傅里叶域是从复数的角度来考虑的，频率轴是以jω为变量，注意是复数j与频率ω的乘积，而频域仅考虑频率ω。时域信号通过拉普拉斯变换到拉氏域，拉氏域通过拉氏逆变换到时域。而傅里叶域只是拉氏域的一个子集，当我们想由频响函数获得模态参数时，需要对频响函数进行曲线拟合得到模态参数：极点和留数，那么此时实际上是从频域变换（曲线拟合）到拉氏域。另一方面，时域用于表征发生的事件，在频域能表征事件的周期特点，而拉氏域用极点和留数来描述系统，三者的关系如图5-22所示。

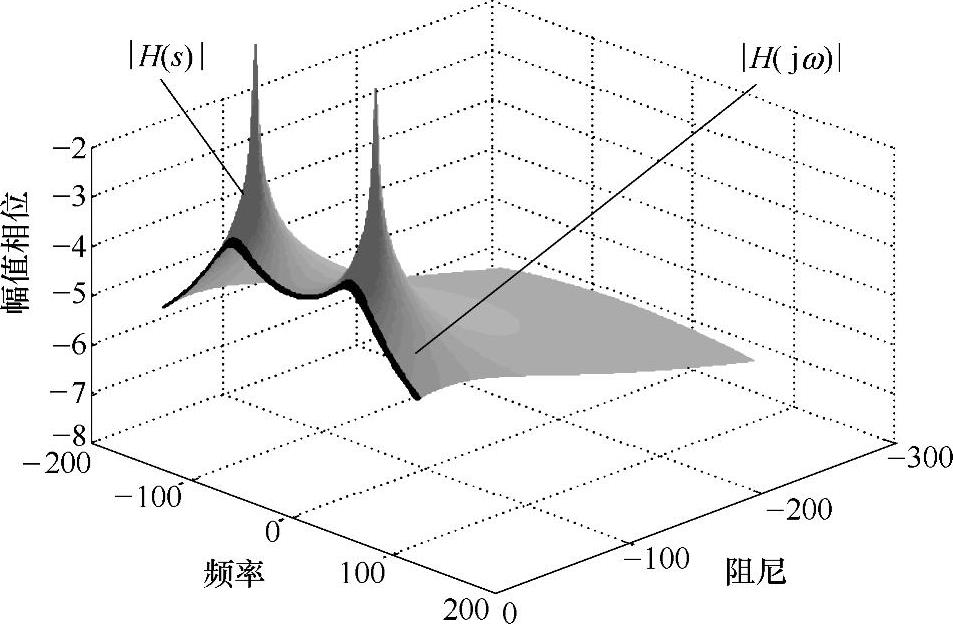
图5-21 系统传递函数（幅值）和频响函数

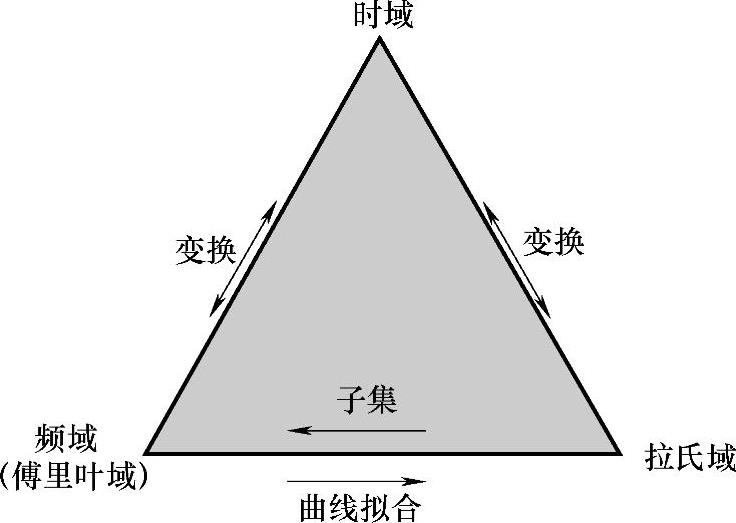
图5-22 三个域之间的关系

另外，传递函数表示的是输出与输入之比，不仅仅用于模态分析，还可用于其他领域，可用于为任何信号生成传递函数。测量信号可以是一般的信号，如电路分析、声学测量、传导性测量等。自变量的取值可以是复平面上任意实部与虚部，并且实部与虚部可以表征任何物理量。

频响函数是响应与激励之比。响应是振动、噪声或应变信号，输入信号为力、体积加速度等，频响函数的取值只是虚部，虚部表示的物理量一定是频率，而非其他物理量。

频响函数FRF是输出与输入之比，而传递率是响应与参考点响应之比（这个传递率与悬置隔振的传递率是不同的概念，关于悬置隔振传递率的定义见后文）。在这里的传递率定义如下，也就是响应和参考点响应的互谱与参考响应点的自谱之比：(www.xing528.com)

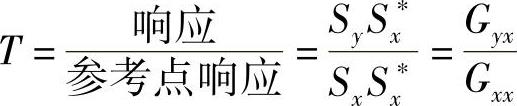
许多时候在一些不同的情况下，是需要测量传递率的。这可能是基于这样的事实，在大型振动台上对产品进行可靠性测试，测试对象安装在大型振动台上，测试件上所有的加速度计测量的数据是相对于输入到被测试件上的参考加速度（参考响应点）。

或者测试是这样进行的，设备处于运行状态，输入力无法测量，只能使用加速度计测量结构的响应。当进行飞行试验、车辆试验、悬架试验或者其他类似试验时，这类测试很常见。这时只有响应数据是可用的，如我们通常所说的工作模态分析，但这有一些轻微的差异，需要我们注意。

另一种情况是OPA/OTPA分析时，由于测量的所有数据都是工作数据，需要计算各路径到目标点之间的传递率，用于计算各路径的贡献量。这种方式下的某个传递率如图5-23所示。注意到图5-23中左侧的单位是Pa/g，这是因为目标点是噪声，路径点处则为加速度。

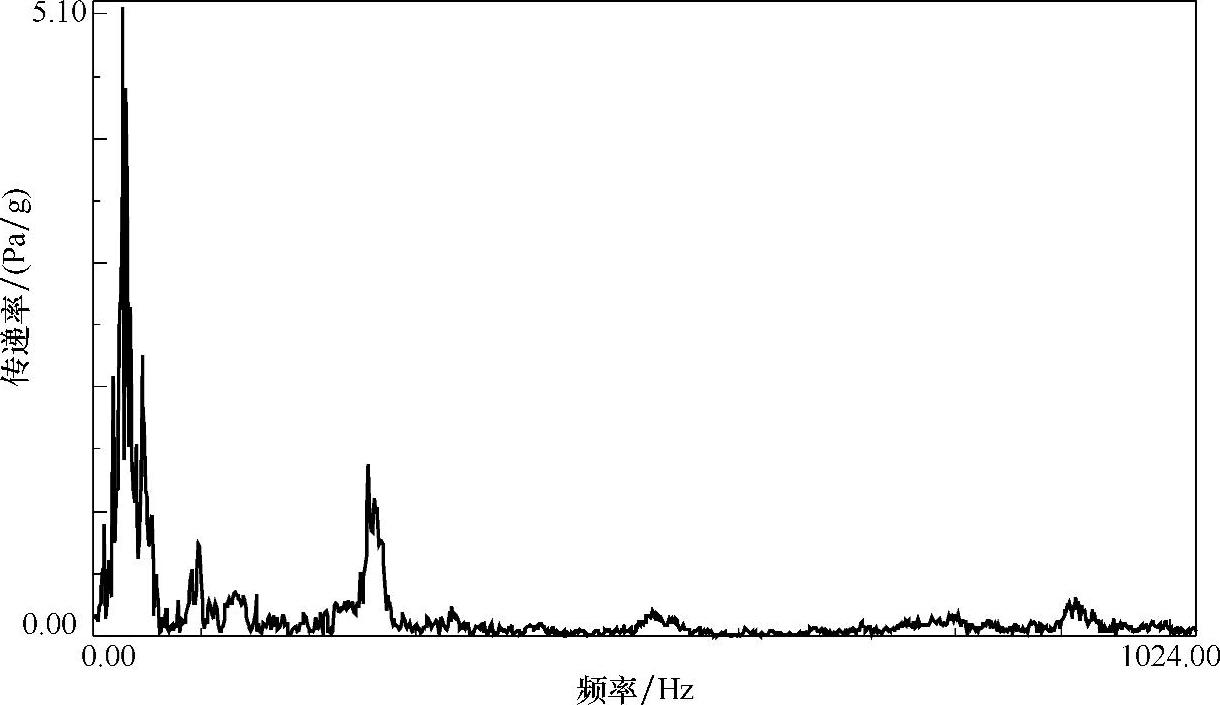
图5-23 某个传递率曲线

很多情况下，人们不区分传递函数和频响函数，实质上测量的是频响函数，但是人们已经习惯称之为传递函数了。特别是在进行灵敏度分析时，有几类常用的频响函数如力振传函、力声传函、声声传函等，这些实质上是频响函数，但人们仍习惯称它们为传递函数。

灵敏度分析常用的几类传函如下：

力振传函VTF：在主要路径位置，如悬置安装位置、排气系统挂钩处进行激励，测量关键点的振动（如方向盘、座椅导轨的振动），得到振动与激励力之间的传递函数。

力声传函NTF：在主要路径位置，如悬置安装位置、排气系统挂钩处进行激励，测量耳旁噪声，得到声压与激励力之间的传递函数。通常要控制该值在一定范围内，对多数轿车而言，目标值一般设定为55dB/N。

声声传函P/P：指声音对声音的传递函数，如进气管口噪声、排气尾管噪声和发动机辐射噪声对耳旁噪声的传函。在空气声定量分析ASQ模型中就要用到该类传函。另外，在进行声腔模态分析时，用到的也是该类传函。

源点动刚度IPI：同一位置的激励力与位移之比，主要测量车身接附点处的源点动刚度，如车身与发动机、悬架连接处、排气挂钩处等位置的局部动刚度，考虑的是在所关注的频率范围内该接附点局部区域的刚度水平，过低必会引起更大的噪声，因此，该性能指标对整车的NVH性能有较大的影响。

传递率：通常用于评价隔振元件的隔振效果，传递率是指主动侧的振动大小与被动侧的振动大小的比值。传递率越大，隔振装置的隔振效果就越好。并且通常采用加速度（主动侧加速度a_a，被动侧加速度a_p）来计算传递率，用分贝形式来表示如下：

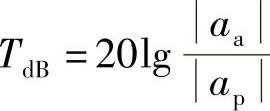
通常当传递率大于20dB时，这个隔振装置被认为是满足要求的隔振装置。传递率大于20dB意味着加速度从主动侧传递到被动侧要衰减90%，被动侧的加速度仅为主动侧加速度的0.1倍。这些单条或多条传函，常规的显示是二维图。如图5-24所示为单条力声传函。

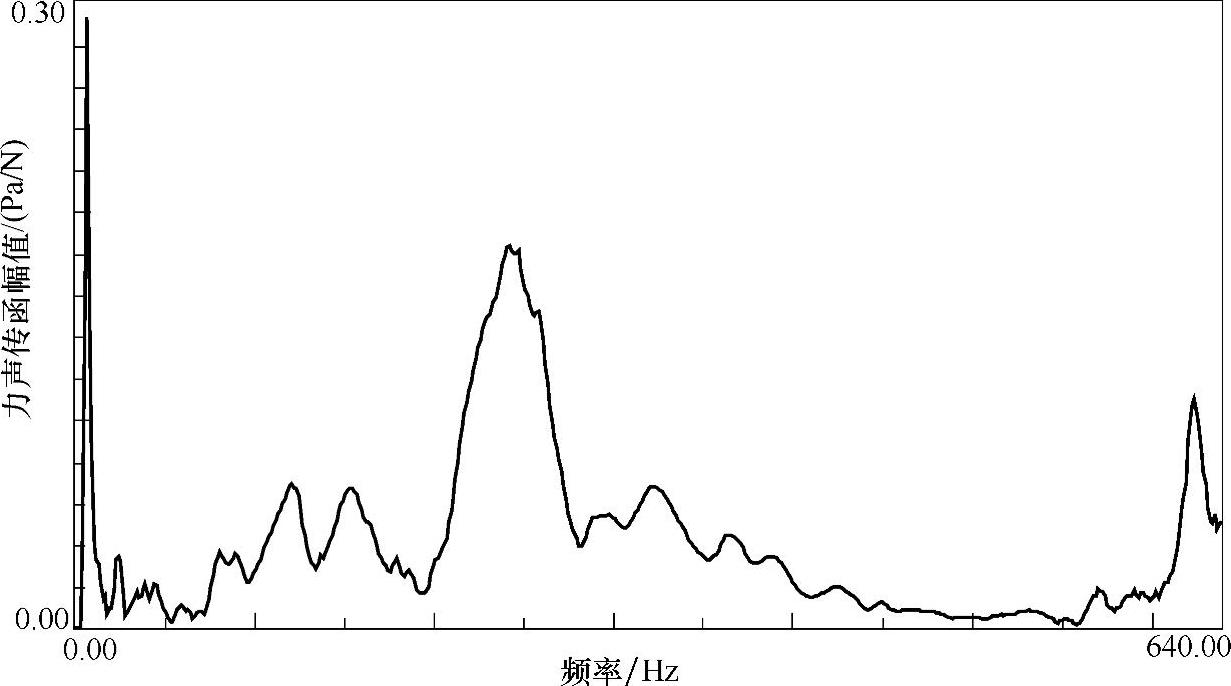
图5-24 单条力声传函

除按常规的二维图显示之外，还可以用彩图显示，如图5-25所示为15个路径处的力声灵敏度。其中最顶上的传函即是图5-24中所示的单条力声传函。当采用这种方式显示时，很容易找到每个频率下最敏感的路径。因此，在TPA分析中多用这种显示方式。

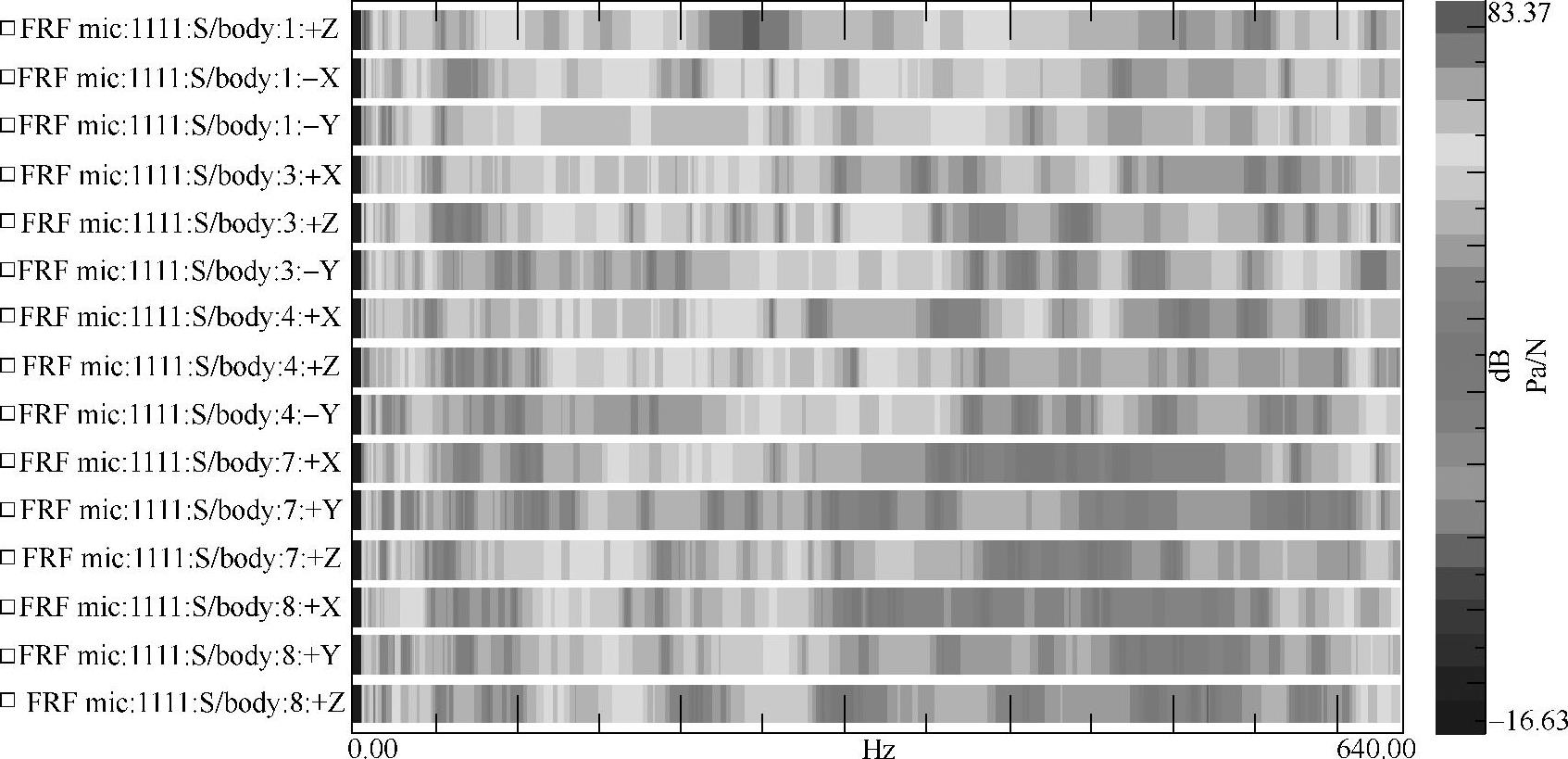
图5-25 彩图显示多条路径的传递函数