如何对MIMO方式下的FRF进行计算？

对于SISO或SIMO测试方式下的频响函数计算，无论是锤击法测试还是激振器测试，都需将捕捉到的时域数据通过FFT变换到频域。FFT变换提供输入和输出信号的线性傅里叶频谱。然后计算输入自谱G_xx、输出自谱G_yy和输入-输出的互谱G_yx。这三个谱函数使用各自的数据纪录进行平均（假设平均N次）。

得到G_xx、G_yx和G_yy后就可计算频响函数和相干了。虽然频响函数可以使用不同形式的估计，但当今绝大多数单输入模态测试中，H₁是频响函数最常用的估计形式，计算过程如图5-13所示。

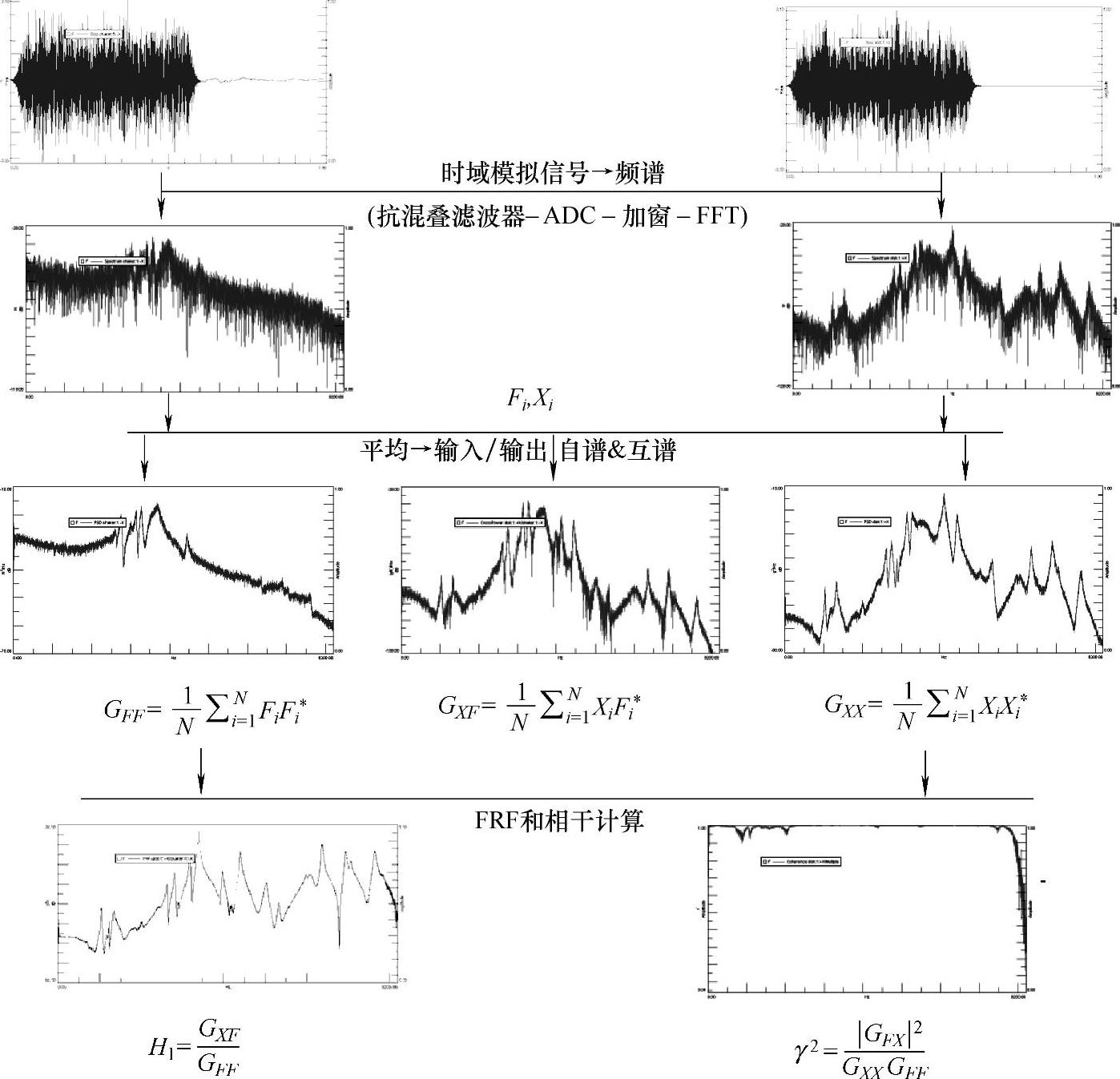
图5-13 单点激励FRF计算过程

单个激励源的FRF计算相对来说比较简单，得到的相干也是我们通常意义上的常相干。但若是多个激励源，FRF计算则要复杂得多，得到的不再是我们常用的常相干了，有可能是重相干，也有可能是偏相干，视商业软件而定。如LMSTest.Lab中则为重相干，关于这一点，下文会有简单介绍。

当用两个或两个以上的激励源时，通常是使用激振器进行测试，采用的方式是MIMO。而对于MIMO方式下的频响函数计算，由于每一个测点位置的响应来自多个激励力的作用，因此，计算FRF时，有别于单激励力下的FRF计算。

现假设2个激励源，对应为1#和2#，计算第i个测点位置的FRF，平均50次，则未知量为H_i1和H_i2。假若两个激励力是线性无关的，此时2个未知量至少需要2个方程，也就是需要平均2次才能求解出这2个FRF，并且要求这两次平均是线性无关的。

现实中，这两次不可能是完全线性无关的，因此需要更多的平均。另外，结构可能存在轻微非线性，多次平均可以起到平均掉轻微非线性和去噪的功能。若平均50次，求出50次平均下的两个FRF后，最后通过最小二乘拟合方法得到最终的两个未知的频响函数H_i1和H_i2，见表5-3。(www.xing528.com)

表5-3 两个激励下的FRF计算公式

重相干描述单一信号（输出谱）与另外一组视为参考信号（输入谱）之间的因果关系，它等于由多个输入信号引起的输出信号的能量与该组输出信号的总能量之比。

假设有2个激励信号，在某一测点的响应来自这两个激励源引起的响应之和。那么重相干是这个响应与这两个激励的总能量之比。因此，重相干的数量与响应测量自由度的数量相同。如图5-14所示，有两个激励源，因此，这个测点有两个FRF，但是重相干数量为1。

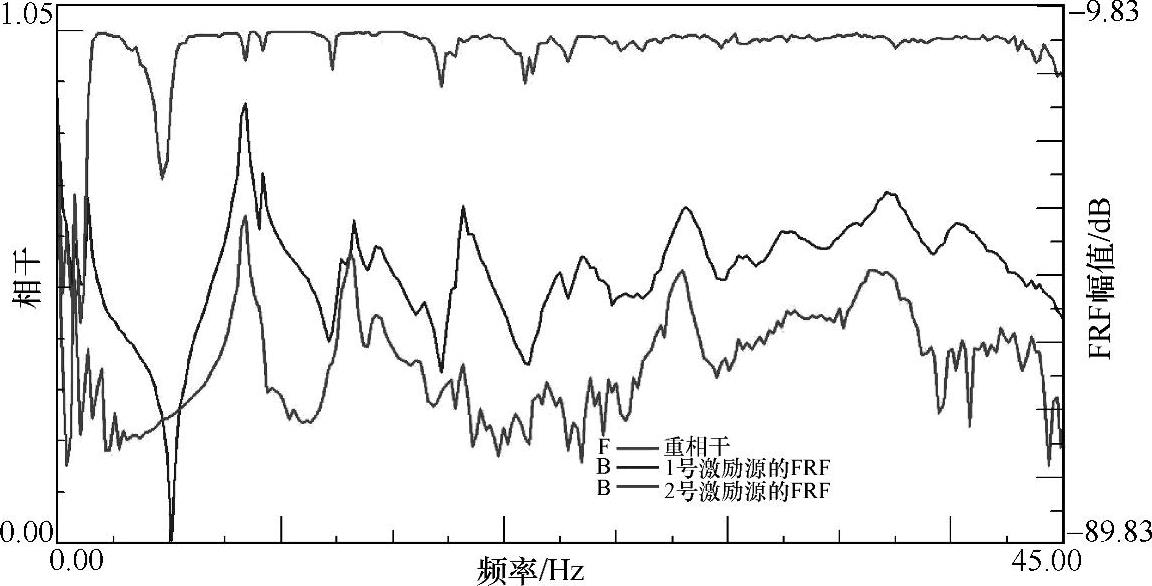
图5-14 两个激励源下的重相干

偏相干则是计算各自激励引起的响应与自身激励之比。假设某一测点既有1#激励源引起的响应，又有2#激励源引起的响应，则偏相干需要分别计算由1#激励引起的响应与1#激励之比和由2#激励引起的响应与2#激励之比。因此，偏相干的数量等于测量自由度乘以激励源数目。