NVH低阶模态为何备受关注？

通过4.1什么是固有频率一节，我们已经明白一个自由度对应一阶模态或固有频率，由于现实世界中的结构多半为弹性体（或称为连续体），因此，结构存在无穷多阶模态或固有频率。既然结构存在无穷多阶模态或固有频率，为什么实际测量或分析时我们只关心低阶的模态或固有频率呢？

我们当然可以说结构的固有频率越低，越容易被外界激励起来。例如，一座桥梁，如果行军的部队按踢正步的姿势行军过桥，那么桥梁就有可能被激励起来产生共振，这是因为行军踢正步的频率与桥梁的某一阶固有频率非常接近或者一致了。另一方面，现实世界中的大多数激励也是低频激励。因此，我们总是可以说结构的固有频率越低，越容易被外界激励起来，所以我们只关心低阶的固有频率。

以上的解释没有问题，但在此笔者要引入“模态有效质量”来说明这个问题。模态有效质量提供了一种用于判断模态“重要性”的方法。若一阶模态包含相当高的有效质量，则其很容易被外界激励起来。另一方面，若一阶模态包含较低的有效质量，则其很难被外界激励起来。

当你对一个结构进行计算模态分析时，你需要确定这个问题：提取多少阶模态是足够的？假设你提取的模态的总的有效质量超过结构实际质量的90%，那么可以说你提取的模态阶数是足够的。即使是试验模态分析，也面临同样的问题：到底获得多少阶模态才合适。

对于一个无阻尼多自由系统而言，通常将描述系统特征的运动方程组用矩阵形式表示：

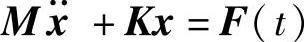
这里M和K分别表示质量矩阵和刚度矩阵，连同相应的加速度向量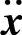和位移向量x以及外力向量F（t）一起组成运动方程。对上式进行特征值求解，可以求得各个特征值与特征向量。特征值即是固有频率，特征向量即是这阶固有频率对应的模态振型ϕ。这个系统的广义质量矩阵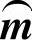定义如下：

定义一个系数向量L：

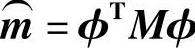
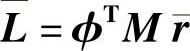
式中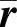，称为影响向量，表示的是在基础上应用单位静态位移引起各质量单元的位移。

对于第i阶模态，其模态参与因子Γ_i定义如下：

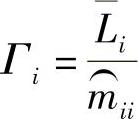
因而，对于第i阶模态，其模态有效质量m_eff，i定义如下：(www.xing528.com)

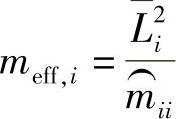
由以上定义可知，每一阶模态的广义质量和有效质量都是不相同的，每阶模态都有自己的有效质量，且每阶模态的有效质量都小于结构的总质量。所有模态的有效质量之和等于结构的总质量，通过模态有效质量可以判定各阶模态的“重要性”，即模态有效质量越大，越重要。

考虑如图5-1所示的悬臂梁结构的横向弯曲振动，悬臂梁长度为L，单位长度上的质量为ρ，弹性模量为E，横截面积为A。根据以上理论，可以得到如表5-1所列的悬臂梁的前四阶模态固有频率、参与因子和模态有效质量。

图5-1 悬臂梁

表5-1 悬臂梁横向前四阶模态相关参数

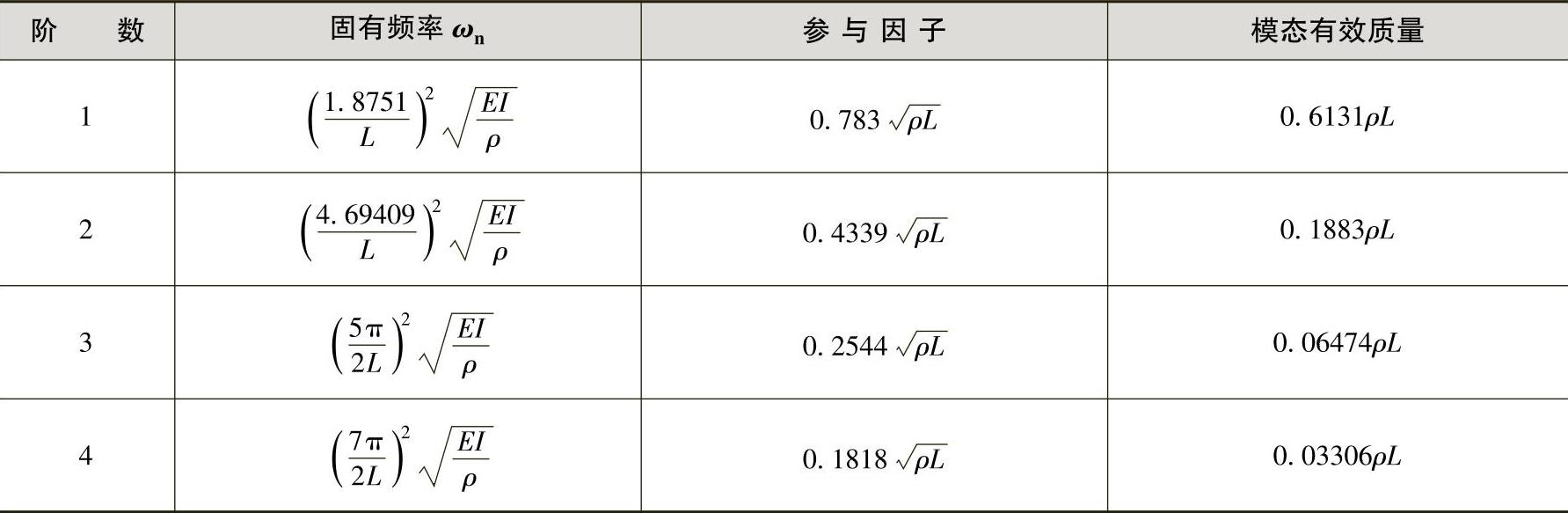
从表5-1中可以看出，模态阶数越低，模态有效质量越大，因而，越低阶模态越重要，越容易被外界激励起来。前四阶模态有效质量之和为0.8992ρL，占结构总质量的89.92%，因此，对于这个结构而言，如果关心横向弯曲振动，提取前四阶模态已足够。

我们再来考虑图5-1所示悬臂梁的纵向振动，假设在自由端作用一个常力P，在t=0时刻突然释放，根据振动理论，其自由端的运动方程为

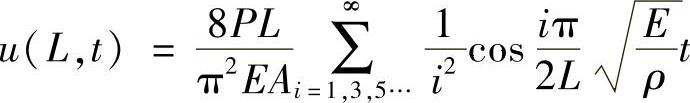
式中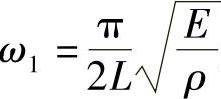，为悬臂梁纵向的第1阶固有频率。对于第k阶模态而言，其响应因子为1/（2k-1）2。因此，各阶模态的响应因子1/（2k-1）2随着阶数k的增大而减少。因此，响应因子越大，响应越大，这阶模态越重要。将各阶模态响应按响应因子来表征其重要性，结果如图5-2所示。从图5-2中可以看出，阶数越低，响应越大，越重要。而其他结构的响应也具有这样的普遍性，所以工程上一般仅关心低阶模态或固有频率。

图5-2 悬臂梁纵向振动响应各阶的重要性