介绍各种激励信号优化方案

不确定性（或随机）激励信号包括随机信号、伪随机信号、猝发随机信号和周期随机信号。确定性激励信号包括正弦信号、猝发正弦信号、正弦快扫信号、正弦扫频信号和步进正弦信号等。理解这两类信号之间的不同之处，以及每种激励信号的优缺点有助于帮助我们决定哪种激励方式将提供最佳的测量。

首先，考虑随机信号，又称为白噪声信号，由于它易于实现，因此是最常用的激励技术，现今广泛用于普通的振动测试。随机信号的随机特性是信号的频率成分、幅值和相位完全随机，每一帧信号都不相同，不具有周期性，如图4-100所示（不同的颜色表示不同的信号）。随机信号包含关心频带内的所有频率成分，但任一时刻，这些频率成分都是随机的，且任何频率成分所包含的能量相等。随机信号的幅值和相位随采集到的平均值的变化而变化，这样易于平均掉结构中可能存在的任何轻微非线性（因为幅值有变化）。

图4-100 随机激励信号

虽然随机激励能平均掉结构存在的轻微非线性，这是有利的一面，但是随机信号从不满足FFT变换的周期性要求，因而泄漏是个极其严重的问题，这就导致采用随机激励会降低数据质量。甚至施加汉宁窗，相应的FRF仍然存在泄漏，FRF峰值幅值仍将受到影响。由于泄漏和窗函数的影响，使得结构看起来像是个大阻尼结构，因此，随机激励下阻尼是一种过估计。图4-101所示为相应于图4-100的频响函数和相干。注意相干在系统共振频率处有突变下降尖峰，这是随机激励显著的特征。

使用随机激励经过多次平均可消除噪声的干扰和非线性的影响，能得到线性估计较好的FRF，图4-102所示为平均3次、10次、20次和40次的结果。从图4-102中可以看出平均次数越多，得到的FRF和相干数据质量越高。

图4-101 加汉宁窗的随机激励（平均10次）

图4-102 不同平均次数的影响

a）平均3次 b）平均10次 c）平均20次 d）平均40次

由于随机激励不满足FFT变换要求，汉宁窗总是需要的。当施加汉宁窗之后，可减少FRF的能量拖尾现象，相干函数也有显著提高，如图4-103所示为施加汉宁窗和不施加汉宁窗的数据经过40次平均之后的结果。窗函数对小阻尼结构影响会更明显。尽管随机激励仍经常使用，但是对于获得模态测试所需的FRF而言，随机激励并不是最佳的激励技术之一。因此，模态测试很少用随机激励信号。

伪随机激励信号是感兴趣频带内的一组频率谱线通过傅里叶逆变换（IFT）到时域，产生激励信号的一种激励技术。因为伪随机激励信号本质上是正弦信号，倘若激励时间足够长，能得到系统的稳态响应，则不存在泄漏。这就证明了伪随机激励是一种非常有用的激励技术。然而，因为激励信号是重复的，如图4-104所示（注意不同数据块的激励信号颜色相同），所以系统将以一种确定的方式进行响应。伪随机信号的频率成分和幅值大小是确定的，相位随机。由于幅值大小是确定的，这将不能平均系统中可能存在的任何轻微非线性。由于本质上是正弦信号，且各帧数据相同，也就是信号是重复出现的，因此不存在泄漏，无须加窗函数。对于线性系统，伪随机激励效果突出。如果要突出非线性特征，也可以使用伪随机激励。

图4-103 汉宁窗的影响

a）FRF b）相干

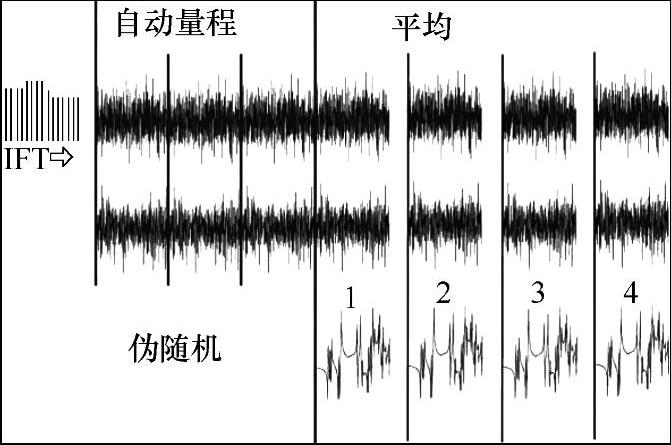
图4-104 典型的伪随机激励信号

猝发随机激励信号与随机激励唯一不同之处在于数据采集过程中只使用了一部分随机信号，如果采用预触发延迟（让信号有时间淡入淡出），那么猝发随机信号在一个采样周期内能完全观测到。如果激励信号和响应在信号采样周期内能完全观测到，那么猝发随机信号满足FFT变换的周期性要求。这意味着信号不存在泄漏也不需要加窗函数。对于大多数结构而言，这一点很容易实现。猝发随机激励信号的猝发时间长短与结构的阻尼有关，如果是小阻尼结构，那么猝发时间可以短一些，即尽快结束激励，使响应有足够的时间衰减，以满足FFT变换要求。如果结构是大阻尼结构，那么猝发时间可以长一些。因此，试验时需要不断尝试，以确定合理的猝发时间。由于信号幅值是随机的，所以可以平均掉测量中可能存在的轻微非线性。猝发随机激励技术集成了随机激励和伪随机激励两者的优点。图4-105所示为一次典型的这类信号的时域测量。注意到中断激励是为了确保响应信号在采样周期内衰减到零。图4-106所示为相应于图4-105的FRF和相干。与随机激励得到的图4-101相比较，注意到FRF和相干有明显的改善，峰值更陡峭、更清晰，共振峰处的相干也特别好。但由于猝发随机只占满部分采样周期，所以激励能量比随机激励偏小。

周期随机激励信号也是感兴趣频带内的一组频率谱线通过傅里叶逆变换到时域，产生激励信号的一种激励技术。它与伪随机的区别在于，伪随机信号的频率成分和幅值是确定的，只有相位是随机，而周期随机只有频率成分是确定的，幅值和相位都是随机的。因此，周期随机是一种统计特性变化的伪随机信号。在每一个周期内，都是一种伪随机信号，但是各个周期内的伪随机信号统计特性不同，即各周期内的伪随机信号互不相关。周期随机信号综合了随机信号和伪随机信号的优点，既有周期性，又具有随机性，从而也避免了两种信号的缺点。利用周期性，可以消除泄漏误差。利用随机性，可以采用多次平均减少噪声和平均结构中存在的非线性。周期随机激励最大的缺点是其比随机激励和伪随机激励都要慢一些，是上述所有类型随机激励信号中用时最长的。如图4-107所示，周期随机激励信号在采集用于计算FRF的数据块之前，还存在多帧延迟数据块，用于消除信号中的瞬态信号，这将导致这种激励技术用时加长。另一方面，周期随机信号因为重复出现，所以满足FFT变换要求，不存在泄漏，无须加窗函数。

图4-105 典型的猝发随机测量序列

(www.xing528.com)

图4-106 猝发随机激励得到的FRF和相干（平均10次）

图4-107 典型的周期随机激励信号

以上各种激励信号都是不确定性信号，接下来将介绍确定性信号。最典型的确定性信号是正弦信号，频率成分单一，如果采样周期刚好是信号周期的整数倍，那么信号满足FFT变换要求，不存在泄漏，无须加窗函数。由于正弦激励不是宽带激励信号，通常只用于某些特殊情况下：

1）用于移除非线性，当对具有强非线性的结构进行模态测试时，可用一个激振器使用低频正弦激励信号移除这个非线性，而其他的激振器使用其他激励信号，如猝发随机激励，这样得到的测量更具有线性特点。

2）仅激励某一阶模态。

猝发正弦的特征类似正弦激励信号，只不过猝发正弦信号也存在一定的猝发时间，如图4-108所示。

图4-108 猝发正弦信号

正弦快速扫频激励信号是在一个采样周期内，信号从低频快速扫到高频的一种快速扫频激励方式。信号重复出现，如图4-109所示，因而满足FFT变换的周期性要求。这意味着信号不存在泄漏，无须加窗。当然，信号必须连续，以便结构获得稳态响应。这种激励技术的优缺点非常类似于伪随机激励技术。正弦快速扫频激励得到的测量结果非常类似猝发随机激励。一个额外的优点是输入力的大小可以控制，通过改变作用在系统上的输入力的量级，使用这种激励技术可以很容易地对结构进行线性检查。由于正弦快速扫频的幅值是确定的，所以不能平均掉结构中可能存在的任何轻微非线性。

正弦扫频信号是按一定的扫频速度从低频扫至高频的激励方式，如图4-110所示，扫频速度可自由设定，因而短时间内能量更集中，激励能量大，可获得更高的信噪比，从而获得更高质量的FRF数据。由于激励能量大，适合于大型结构模态测试。另外，响应信号可分批测量，测量时间比得上猝发随机激励。扫频方式有线性方式和对数方式，如果采用对数方式，低频谱线数量多，高频谱线数量少。如果关心的模态频率范围不大，可采用线性扫频。如果关心模态频率范围较大，对数扫频要更快速有效。

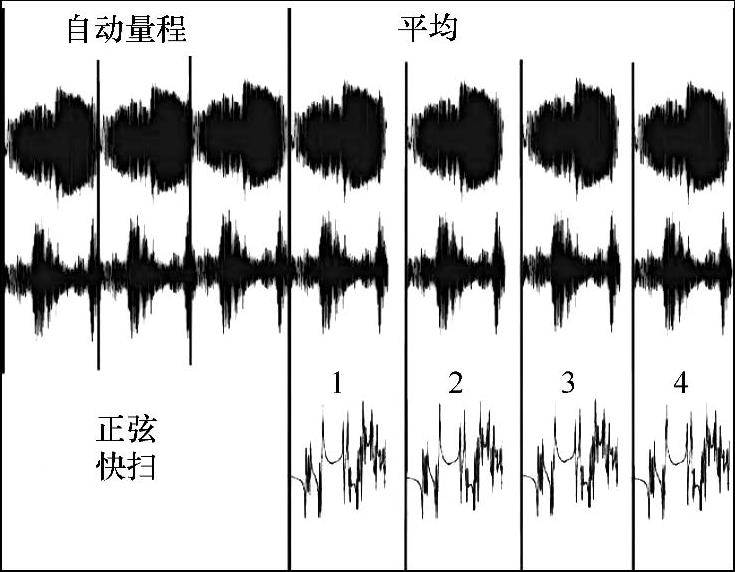
图4-109 正弦快速扫频信号

图4-110 典型的正弦扫频信号

正弦扫频信号的扫频速度对测量结果可能存在影响，特别是针对小阻尼结构，会存在共振峰延迟现象。这是因为小阻尼结构响应衰减时间较长，如果扫频速度过快，将导致共振峰出现偏离实际值的现象出现。如图4-111所示为对一个小阻尼结构采用两种不同的线性扫频速度，可以看出，共振峰出现了明显的偏离。因此，对于正弦扫频激励，需要不断尝试，以确定合适的扫频速率，使结构响应达到稳态。

图4-111 扫频速率对测量的影响

步进正弦激励技术是另一种非常有用的窄带激励技术。任一时刻其激励信号均为单频信号，其频率成分与频谱的谱线重合，通过傅里叶逆变换到时域，如图4-112所示。因为能保证满足FFT变换的周期性要求，所以步进正弦信号无泄漏存在，不需要加窗函数。除了每个时刻只有一个频率激励外，其他特征类似于伪随机激励。但是一个重要的不同之处就是其对信号幅值进行了改进。宽带技术要求模数转化器捕捉到整个频谱范围内信号的所有能量，但是其频率可能具有以下特征：在频谱上幅值变化幅度大。这对步进正弦来说，不成问题，因为任一时刻步进正弦激励方式的激励或（和）响应的所有能量在频谱图中只体现在单条谱线上。因此，激励能量非常大，信噪比高，可获得高质量的FRF。因为它本质上不是带宽激励，所以它是所有激励方式中最慢的（每条谱线都需要单独估计）。由于步进正弦激励用时较长，可通过改变步长来提高测量效率，通常在共振区，步长小，在非共振区，步长长。还有一点值得注意，由于步进正弦激励能量大，为了安全考虑，闭环控制是必须的。由于激励信号的频率和幅值易于控制，对于证明结构的非线性，它的表现又是卓越的，上面所有讨论的激励方式，步进正弦激励可能产生最优的测量结果。

图4-112 典型的数字步进正弦信号