锤击法窗函数优化技巧

锤击法模态测试时，通常应用力窗和指数窗。在许多数据采集系统中，为力脉冲激励部分施加力窗。力窗是单位增益的窗函数，如图4-71所示，作用于脉冲激励发生的那个时段。加力窗是为了消除可能来自于力锤激励通道的噪声。通常，设置力窗的宽度约为数据样本窗口的5%，使得力脉冲完全位于这个单位增益窗内，力窗之外的时域样本纪录则被加权置零。力窗不一定总是必需的，但是几乎所有的数据采集系统都有。需要着重注意的是，力窗从来不能消除测试过程中可能出现的二次连击的影响。使用力窗消除连击所造成的影响，将严重扭曲输入力谱。

锤击法测试是模态测试非常常用的测试方法。它总是会引起一些类型的瞬态响应，而该响应为一系列指数衰减的正弦波的组合。这种情况下，如果能完全捕获到瞬态响应信号，便可满足FFT变换的要求，测量不存在泄漏。但是大多数结构，特别是小阻尼结构，指数衰减响应信号经常在采样时间内基本上没有完全衰减。那么，这就意味着不满足FFT变换的要求。这种情况下，通常为响应信号施加指数窗，加窗后的信号可以更好地满足FFT变换要求，如图4-72所示。

图4-71 力窗

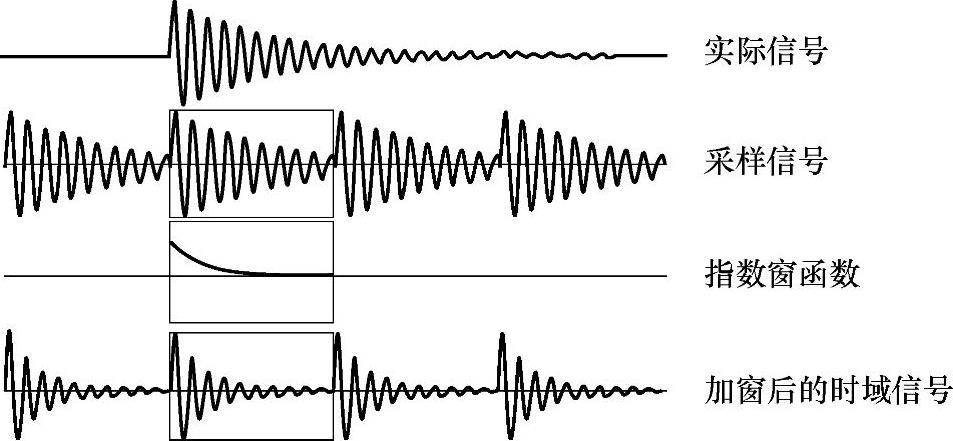
图4-72 指数窗使响应信号满足FFT变换要求(www.xing528.com)

加指数窗的响应能更好地满足FFT处理的要求。这时整个响应信号似乎都可以捕获到，但其实是以加窗为代价的。减少指数窗应用的一个方法是调整测量时间，从而考虑捕获更长的时域数据，或者增加样本总数，其直接效应就是获取更长的时域数据。无论如何，如果信号在采样周期的末端本质上没有衰减到零，那么必须加指数窗，以减少泄漏所造成的影响。

另一方面，如果指数窗使用不合理，将会引起一些问题。如果需要使用迅速衰减的指数窗（大指数窗）以便最小化泄漏所造成的影响，那么你将会冒着丢失密集模态的风险。当必须为数字信号处理使用指数窗时，在估计小阻尼结构和空间上有密集模态时，将会引起一些严重的问题（丢失模态）。虽然加指数窗以最小化泄漏可能是必需的，但是窗的使用可能会隐藏或者扭曲FRF中的模态。故锤击法测试时，当需要使用指数窗时，需要极其小心。

在使用指数窗之前，总是需要考虑的是，增加谱线的条数或者减半带宽，二者本质上都是增加总的采样时间。这种考虑很有帮助，因为这是在考虑系统响应在采样周期结束之前自然地衰减到零。如果这一点能够实现，那么没必要使用指数窗。在应用指数窗之前，应先考虑前面提及的两个方法作为最小化泄漏影响的可能方法。在没有考虑时域响应的情况下，就在测试的第一步任意地加指数窗，这是不推荐的。

各类窗函数都有自己的应用条件，在使用窗函数时必须多加小心。另外，在模态测试过程中尽量提供无泄漏的测量，避免加窗。无泄漏的测量，本质上是设法使信号满足傅里叶变换的要求：要么采集周期信号，要么采集在一个采样间隔内能完全观测到的信号。回想一下，像伪随机、猝发随机、正弦扫频和步进正弦信号，这些信号在大多数情况下都满足这个要求，因而不存在泄漏，也就不必加窗。另外锤击法测试，也有方法（前面提到的）使信号满足FFT变换的要求，无需加窗。