深入了解频谱分析技术Spectrum

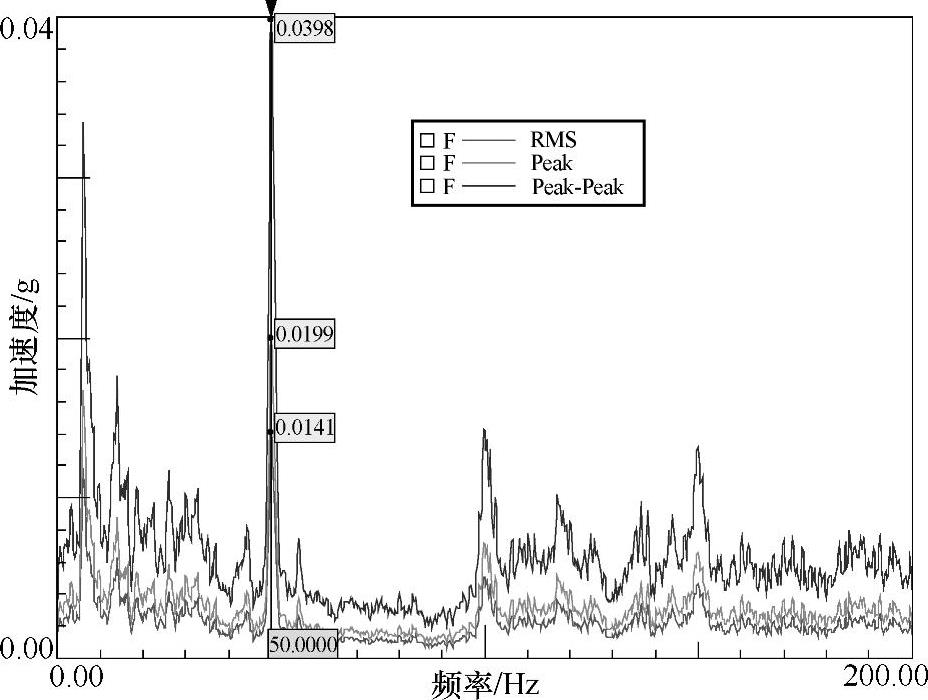
图3-56 三种格式表示同一信号

对时域信号做傅里叶变换得到的直接结果即为频谱Spectrum。它是复数值，因此有幅值和相位信息。同时显示同一频谱的幅值和相位的图形称为波德图（bode），如图3-57所示。

频谱图中的0Hz表示时域信号的平均值或称为直流偏量。频谱只有线性形式，不像自谱有线性形式和平方形式。由于频谱是复数形式，包含相位信息，当信号中包含不相关的噪声成分时，由于噪声成分的相位是杂乱无序的，那么多次线性平均之后，可以将不相关的噪声平均掉。另外，即使是相关的频率成分，如单频信号进行线性平均时，线性平均次数越多，幅值也越趋向于0（关于这一点，请参考本章3.9频谱和线性自功率谱的区别）。

如两个单频信号幅值和频率相同，但相位相反，当对这两个信号进行线性平均时，它们的幅值将为0，如图3-58所示。在汽车排气系统中，有一种主动消音机制，即是先接收声音，然后将声音反相回放回去，从而达到主动消音的目的，利用的就是这个原理。

相对而言，频谱是计算其他谱函数的基础，如计算自谱、互谱和频响函数等，都需要用到频谱。

在频谱的基础上，衍生出了相位参考谱。顾名思义，在计算相位参考谱时，需要选择一个信号作为参考信号，那么与此信号相关的成分将不会被平均掉，而与此信号不相关的成分将会被平均掉。像在做发动机TPA时，经常在发动机上表面安装一个单向的加速度传感器，这个单向加速度传感器信号的作用之一就是用来做相位参考的。(www.xing528.com)

另外，由于频谱还包含相位信息，因此，还可用于ODS分析（工作变形分析）。

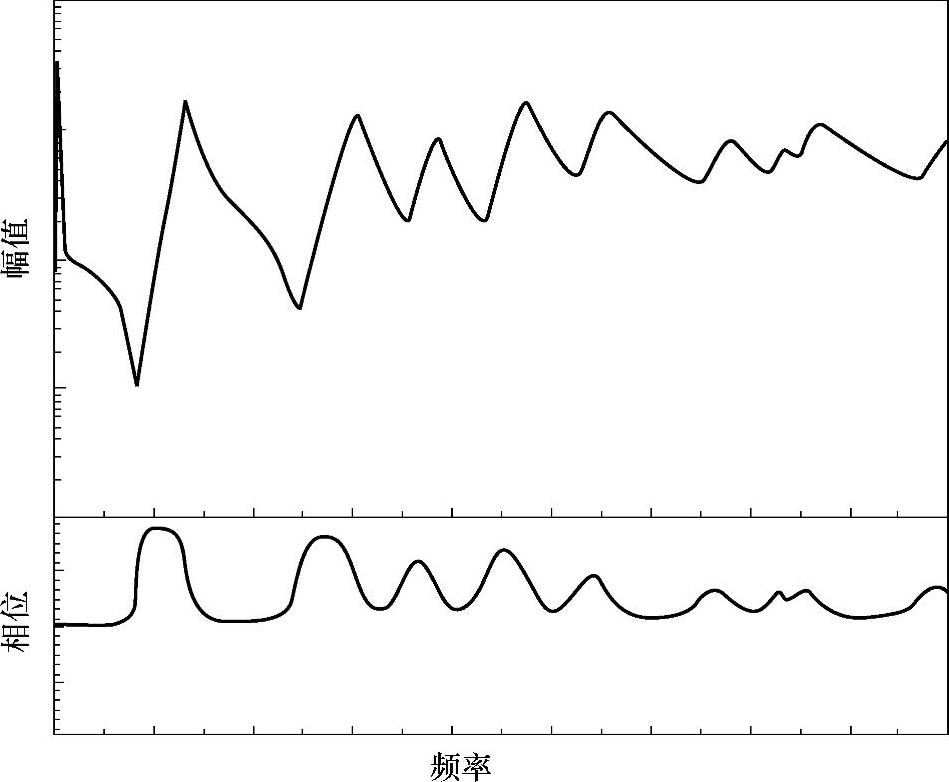
图3-57 波德图

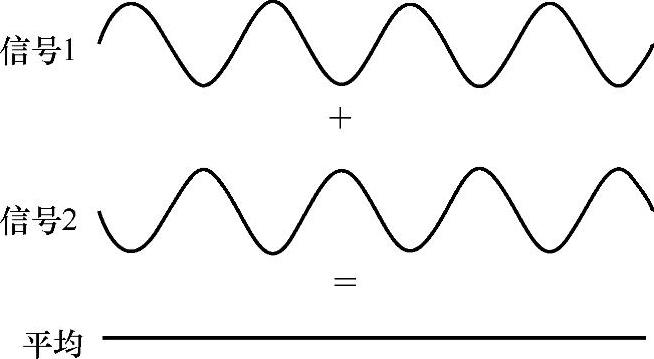
图3-58 两个幅值相同，相位相反的信号平均