【摘要】:如图3-46所示,由于峰值高低不一样,则对应的峰值RMS也不一样。图3-46 加窗对RMS的影响从图3-46可以看出,不同的窗函数,计算19~87Hz内的总有效值都为0.71,因此,对于不同的窗函数,计算总有效值是没有影响的。因此,如果对信号施加了窗函数,则频谱还需要进行修正。每个窗函数对数据的频域描述都有影响。一般而言,窗函数将降低函数峰值幅值的精度,并且使得最终得到的阻尼似乎比实际真实存在的阻尼要更大。
窗函数会使信号幅值失真,那么窗函数对计算RMS是否有影响呢?由于加窗使得频率峰值失真,因此,如果计算峰值处的RMS,必然有影响。如图3-46所示,由于峰值高低不一样,则对应的峰值RMS也不一样。但如果计算窄带RMS或整个频带的总RMS呢?
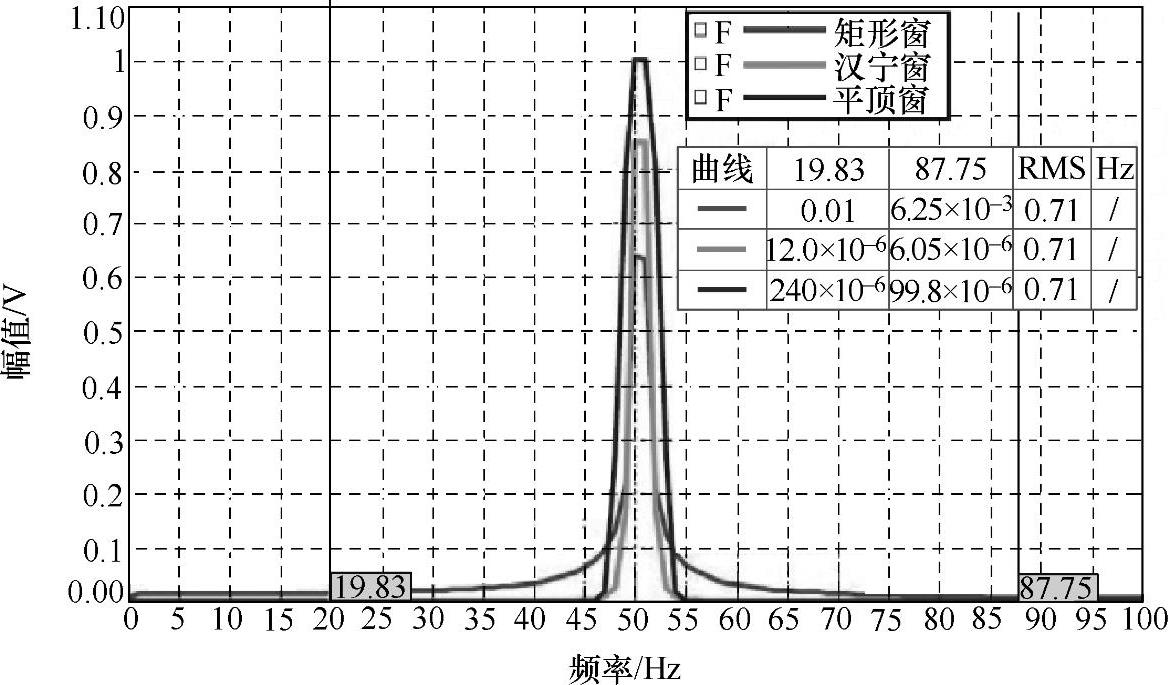
图3-46 加窗对RMS的影响
从图3-46可以看出,不同的窗函数,计算19~87Hz内的总有效值都为0.71,因此,对于不同的窗函数,计算总有效值是没有影响的。因为能量虽然泄漏到旁瓣上,但总的能量是不变的。(https://www.xing528.com)
从第3.6.3小节中对比原始信号和加窗后的信号可以看出,信号的能量在起始和结束位置都计权置零,因而,从能量的角度来考虑,加窗后的信号能量要比加窗之前的能量小。因此,如果对信号施加了窗函数,则频谱还需要进行修正。修正分幅值修正和能量修正,如果是单条谱线则为幅值修正;如果是宽带则为能量修正。但需要记住一点,这个工作,通常商业软件会自动处理,无须人工处理,只需要知道有这么一步工作即可。
如果锤击法测试中,响应在采样结束之前仍未衰减到零,则对响应加指数窗以最小化泄漏是必需的,但是如果加大的指数窗函数扭曲了真实的FRF,会致使在FRF的密集模态很难观测到。因此,指数窗的使用,虽然是数字信号处理必须考虑的事项,但是当估计小阻尼结构和密集模态时,如果使用不当,将会引起一些严重的问题。
每个窗函数对数据的频域描述都有影响。一般而言,窗函数将降低函数峰值幅值的精度,并且使得最终得到的阻尼似乎比实际真实存在的阻尼要更大。尽管这些误差完全是不想要的,但相比泄漏造成的严重失真而言,它们还是更能让人接受的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




