窗函数的时频域特性分析

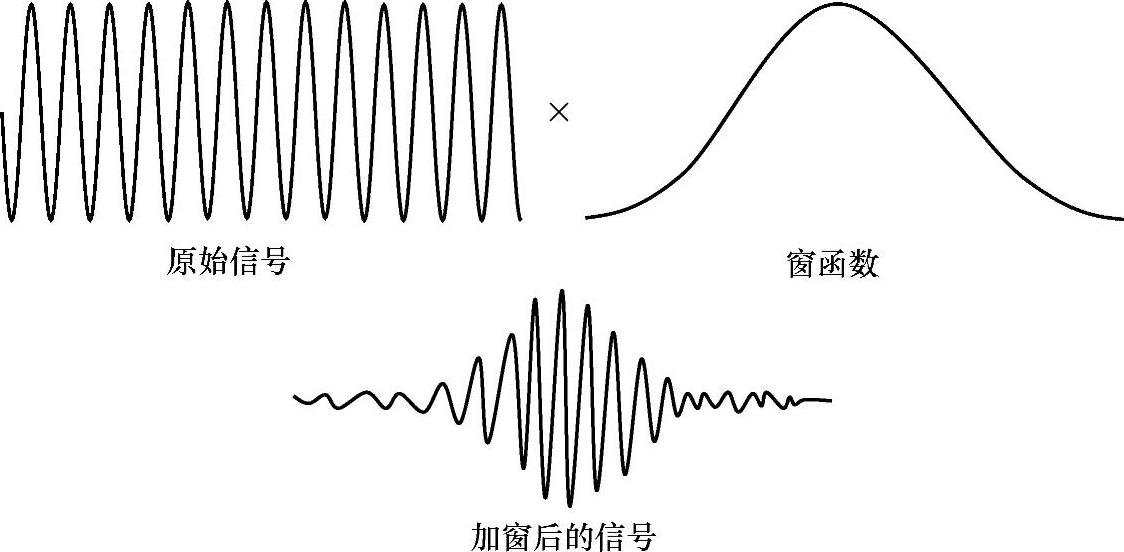
图3-40 加窗过程示意

加窗实质是用一个所谓的窗函数与原始的时域信号做乘积的过程（当然加窗也可以在频域进行，但时域更为普遍），使得相乘后的信号似乎更好地满足傅里叶变换的周期性要求。如图3-40所示，原始的信号是不满足FFT变换的周期性要求的，变换后存在泄漏，如果施加一个窗函数，会在一定程度上减少泄漏。为了减少泄漏，用一个窗函数与原始周期信号相乘，得到加窗后的信号为周期信号，从而满足FFT变换的周期性要求。

使用不同的时间窗，它的时域形状和频域特征是不相同的。在这，介绍三种常见的窗函数的时域表达形式，以及它们的时域窗形状和频域特征。这三种窗分别是矩形窗、汉宁窗和平顶窗。它们的时域表达形式见表3-3，并且假设时间窗的范围为0≤t≤T，如果时间t的取值区间不同，窗函数的表达形式也会略有差异。

表3-3 窗函数的时域表达

矩形窗、汉宁窗和平顶窗的时域形状和频域特征如图3-41所示，可以看出，窗函数不同，时域和频域都是不同的。

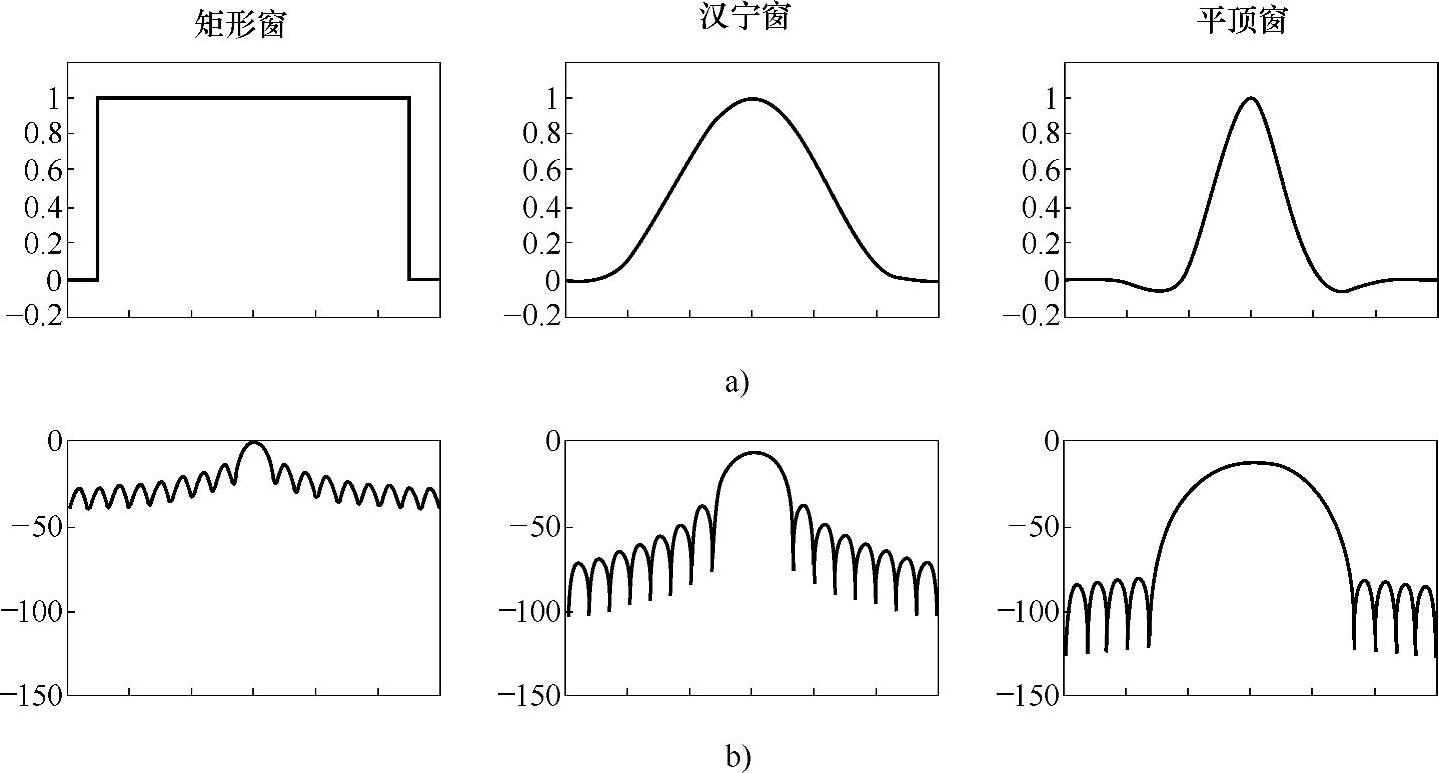
图3-41 三个窗函数的时域形状和频域特征

a）时域形状 b）频谱特征

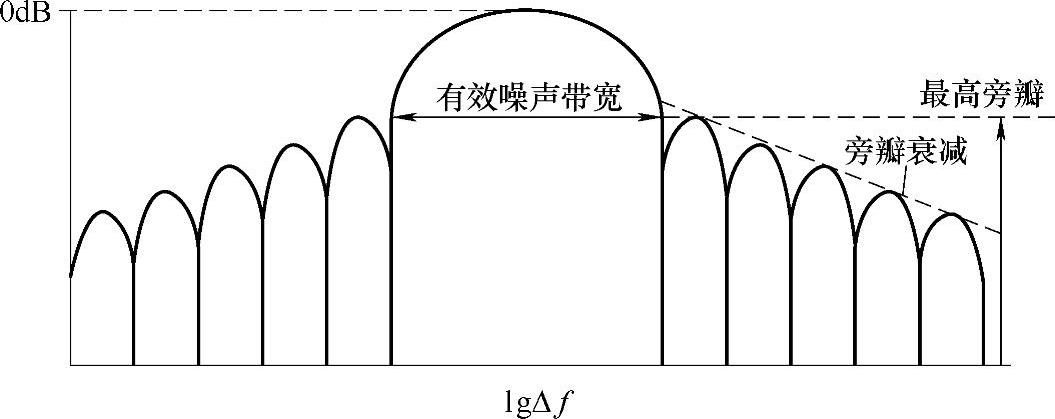
为了减少泄漏，可采用不同的窗函数进行信号截取，因而，泄漏与窗函数的频谱特征相关。窗函数的典型频谱特征如图3-42所示。

(www.xing528.com)

图3-42 窗函数的典型频谱特征

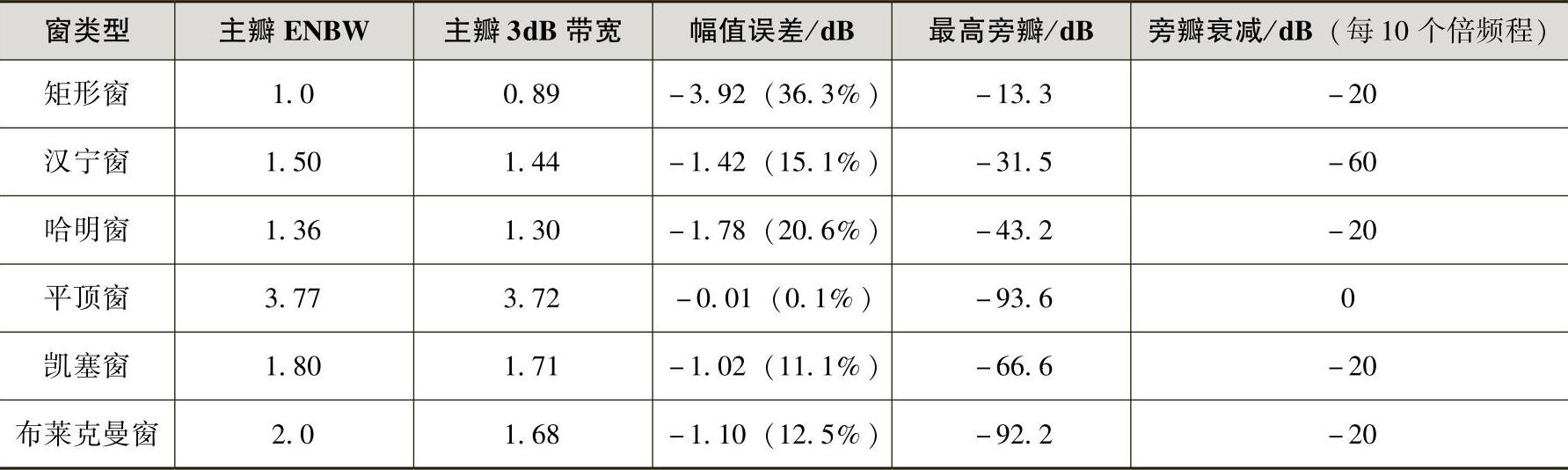
各种窗函数频谱特征的主要差别在于：主瓣宽度（也称为有效噪声带宽，ENBW）、幅值失真度、最高旁瓣高度和旁瓣衰减速率等参数。加窗的主要思路是用比较光滑的窗函数代替截取信号样本的矩形窗函数，也就是对截断后的时域信号进行特定的不等计权，使被截断后的时域波形两端突变变得平滑些，以此压低谱窗的旁瓣。因为旁瓣泄漏量最大，旁瓣小了泄漏也相应减少了。不同的窗函数具有不同的频谱特征，表3-4列出了一些常用窗函数的特征。

表3-4 常用窗函数的特征

主瓣宽度主要影响信号能量分布和频率分辨能力。频率的实际分辨能力为有效噪声带宽乘以频率分辨率。因此，主瓣越宽，有效噪声带宽越宽，在频率分辨率相同的情况下，频率的分辨能力越差。如图3-43所示，红色为平顶窗（3.77Δf），黑色为汉宁窗（1.5Δf），蓝色为信号频率。可以明显看出，主瓣越窄，频率分辨越准确。对于窗函数宽的主瓣而言，若有邻近的小峰值频率，则很难辨别出来。

旁瓣高低及其衰减率影响能量泄漏程度（频谱拖尾效应）。旁瓣越高，说明能量泄漏越严重，衰减越慢，频谱拖尾越严重。对50.5Hz（频率分辨率为1Hz）的信号分别施加矩形窗（红色）、汉宁窗（绿色）和平顶窗（蓝色），用对数显示幅值，加窗后的结果如图3-44所示。从图3-44中可以看出，矩形窗的频谱拖尾更严重，因为矩形窗的最大旁瓣高，旁瓣衰减慢。

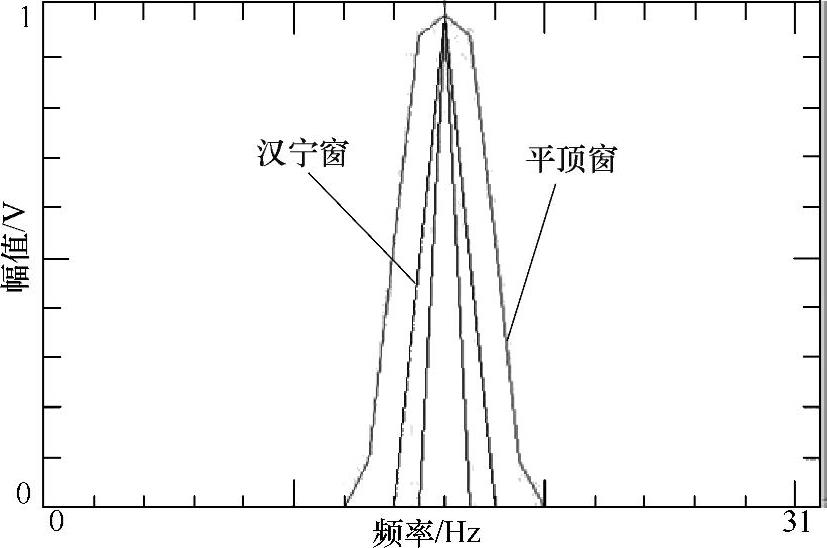
图3-43 加窗会影响频率分辨能力

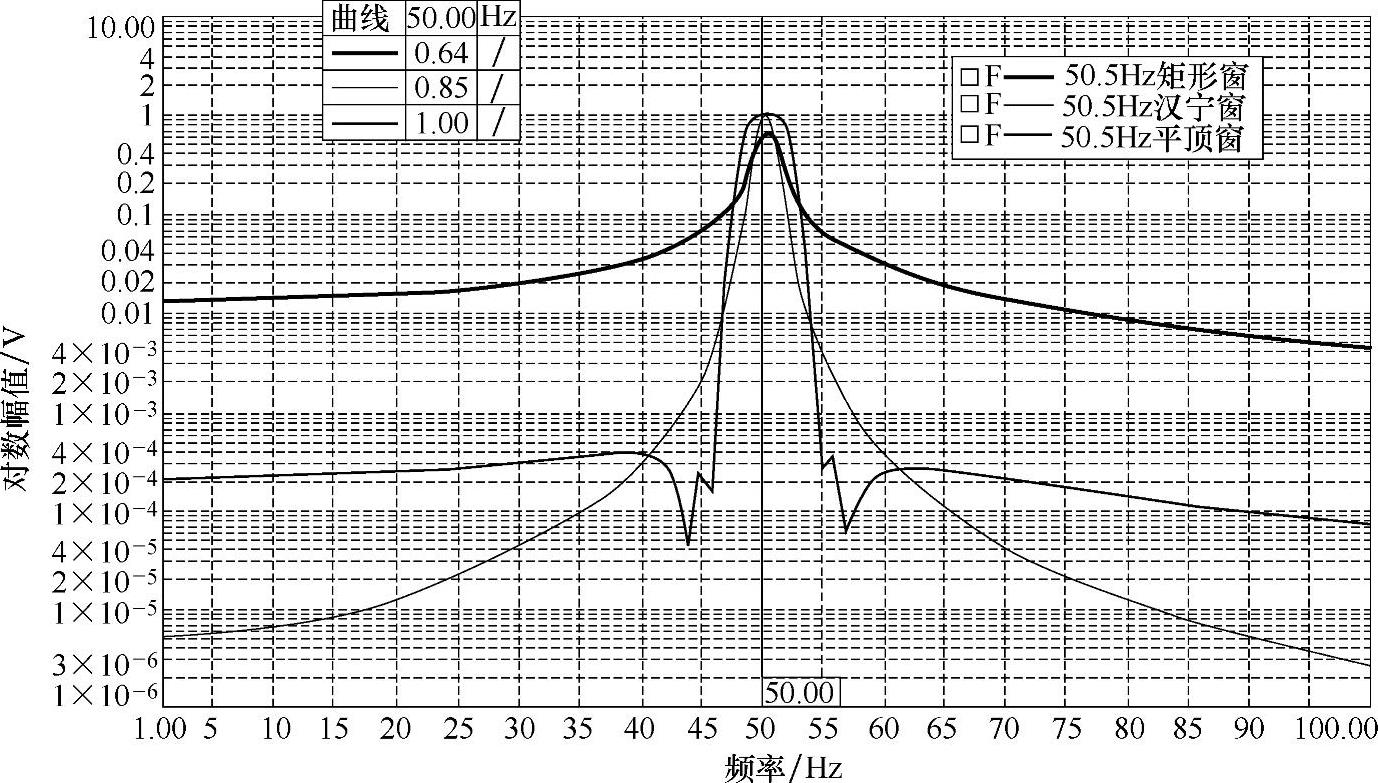
图3-44 三种窗函数的拖尾效应

相对而言，如果旁瓣能量较小，高度趋于零，使得信号能量相对集中于主瓣，则较为接近真实的频谱。不同的窗函数对信号频谱的影响是不一样的，这主要是因为不同的窗函数，产生泄漏的大小不一样，频率分辨能力也不一样。