倘若对一个正弦信号进行采样,如果采样频率等于信号频率,那么采样的时间间隔等于信号周期,因而,信号的每个周期只能采集到一个数据点,如图3-31所示,将这样的采样数据点连成线条,得到的线条将是一条直线,因而,对应的频率成分为0Hz。
如果采样频率为这个正弦信号频率成分的2倍,因而,采样的时间间隔为信号周期的一半,因此,信号每个周期内的采样点数为2个,也就是每个周期采集两个数据点,如图3-32所示。将这些采样点连成线条,得到的信号形状为三角波,虽然信号的频率成分没有失真,但是很难保证信号的幅值不失真。因为这两个采样点很难位于正弦信号的波峰与波谷处。也就是说,在很大程度上,采样后的信号的幅值是失真的。
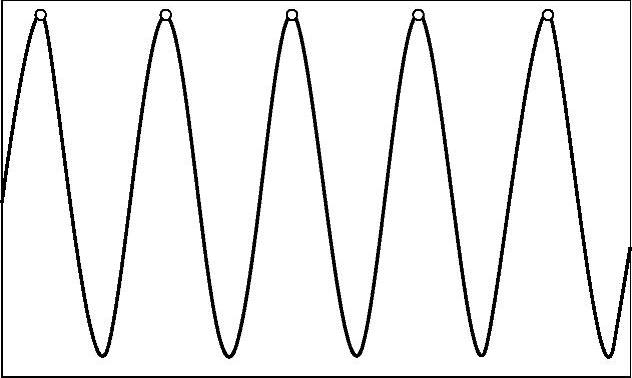
图3-31 采样频率等于信号频率
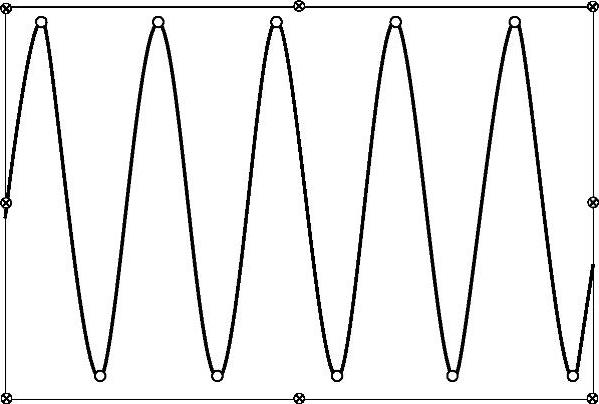
图3-32 采样频率等于信号频率的2倍
通常情况下,若采样频率fs小于2倍的信号频率fa,即fs<2fa,那么,采样后的信号将存在混叠。如图3-33a所示,由于信号中存在超出奈奎斯特频率的信号,采样后的信号将会使超过奈奎斯特频率成分之上的频率关于奈奎斯特频率镜像到奈奎斯特频率以下的可观测区域,如图3-33所示。
在这给出一个扫频的混叠实例。扫频信号为100~600Hz,采样频率为1000Hz,因而可观测到500Hz以内的信号成分。因此,对100~500Hz以内的信号进行采样,FFT变换后的频率是没有问题的,但是对于超出500Hz以上的频率成分(500~600Hz),由于混叠的原因,最终将导致这部分信号混叠成了400~500Hz。(https://www.xing528.com)
用于演示混叠现象的最经典例子之一是所谓的“车轮效应”。在影片里当马车越走越快时,马车车轮似乎越走越慢,然后甚至朝反方向运转。刚开始轮辐逆时针运转,然后逐渐变慢并开始顺时针运转。
与车轮效应相同的是转动的吊扇,小时候都见过家中的吊扇,当转速越来越快时,出现的现象是先顺时针旋转,然后静止,然后逆时针旋转。这是因为人眼在看物体时,人眼也有一定的采样速率。当人眼的采样速率跟不上越来越快的转速时,就会出现混叠现象。静止不动时的转速对应的频率就是人眼的采样速率。
人眼在观看转动的吊扇时,对于倒转现象是因为高速旋转的叶片转速非常快,在短时间内从0°顺时针旋转到330°时(假设的情况),人眼观察到的似乎是从360°逆时针旋转到330°,因此,看起来像是在反转。

图3-33 信号混叠
a)实际信号频率 b)采样后的信号频率
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




