拉普拉斯域与傅里叶域简介

通过上一小节已经明白传递函数和频响函数的区别：传递函数的自变量是实部和虚部，而频响函数的自变量仅仅是虚轴。现在如果我们绘出传递函数所对应的曲线图，该图将映射成一个曲面，因为这个函数是通过两个独立变量σ和ω定义的。因为这些数值是复数，所以，可以分别绘出它们的实部和虚部图，当然也可以绘出函数的幅值和相位图，如图3-14所示。

在这，传递函数的自变量取值是整个复平面，包括实部和虚部，因而，称实部与虚部为自变量的函数所在的域为拉普拉斯域。之所以称为拉普拉斯域是因为对传递函数进行变换的方法是拉普拉斯变换。

如果我们考虑系统传递函数沿jω轴估计的幅值，并且将其投影到沿jω轴的切片平面上，那么我们将看到如图3-14所示的投影切片。而这正好是我们用FFT分析仪测量得到的曲线：频响函数。并且可以看出，这只有一个独立变量jω用于描述频响函数。同时，我们也注意到我们仅用一条曲线，而不是一个曲面来描述系统的频响函数。把以虚部（频率轴）为自变量的函数所在的域称为傅里叶域，之所以称为傅里叶域，是因为变换方法为傅里叶变换。

频响函数是传递函数的特例，实际上我们也可以说傅里叶变换是拉普拉斯变换的特例。传递函数的自变量是整个复平面，也就是拉普拉斯域，而频响函数的自变量仅是沿虚轴，也就是沿频率轴，对应的是傅里叶域。(www.xing528.com)

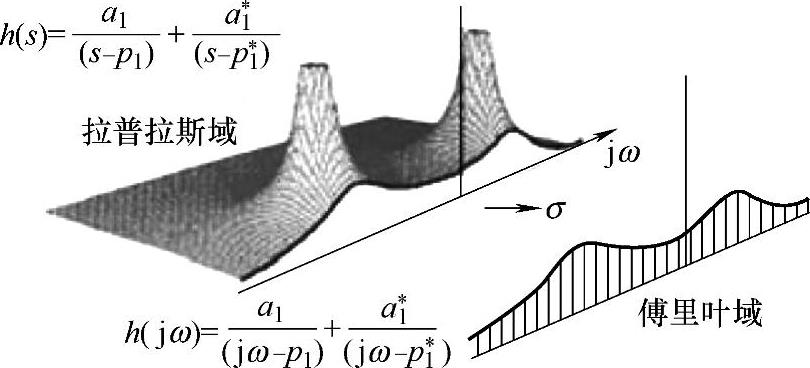
图3-14 拉普拉斯域和傅里叶域

在这你可能会问：傅里叶域不就是沿频率轴变化，那么，它跟频域有什么区别呢？频域仅仅是随频率变化，是从实数的角度来考虑的。而傅里叶域是从复数的角度来考虑的，频率轴是以jω为变量，注意是复数j与频率ω的乘积。