理解量化误差的产生和影响：以实例数据为例

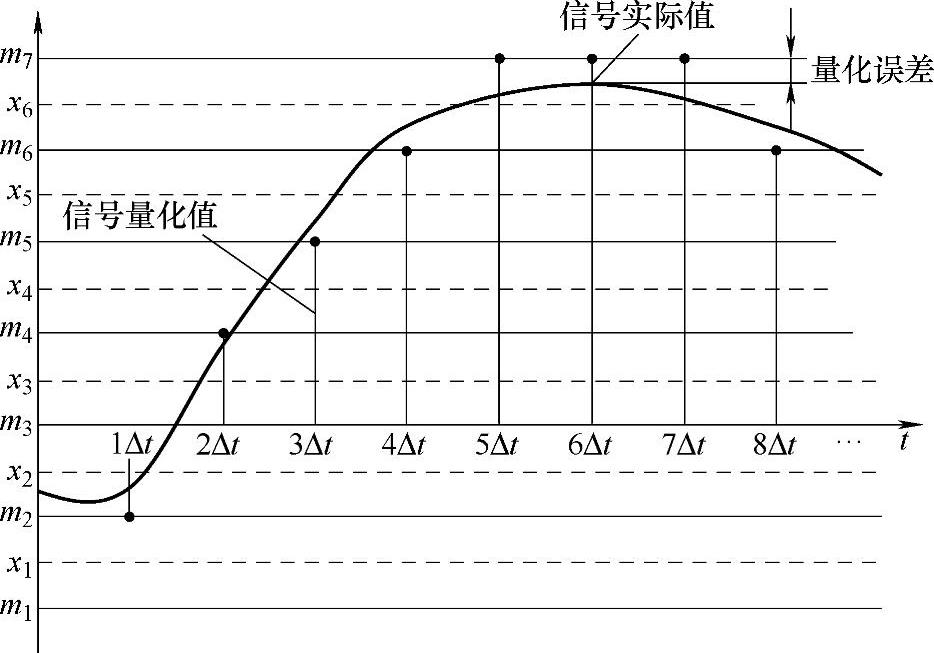
图2-28 量化误差实例说明

量化误差是模数转换过程中另一个重要的幅值误差源，前文2.4节已说明过采样频带也会给幅值带来误差。在模数转换过程中，实际模拟量值与量化数字值之间的差异称为量化误差或量化失真。这个误差归咎于取整（只能是量化量级的整数倍）或截断造成的，误差大小是随机的，在不同的采样点，这个误差大小也不相同。在进行量化时，是将信号的电压幅值按四舍五入的方式量化到最近的量化电平上。在这将通过一个实例数据来说明量化误差是如何产生的。

假设考虑如图2-28所示的采样过程，黑色曲线表示信号实际大小，采样间隔为时间Δt，每个采样点上的黑色实心点表示量化后的幅值。考虑第6个采样点的幅值量化误差。m表示量化电平，x表示相邻两个量化电平的平均值，从图2-28中可以看出，在采集第6个数据点时，信号的实际幅值大小位于量化电平m₆和m₇之间，但这个数据量化之后，幅值要么是m₆，要么是m₇。首先，将该幅值与m₆和m₇的平均值x₆进行比较，发现幅值大于x₆，因此，按四舍五入方式量化到最近的量化电平m₇上，m₇与信号实际值之差即是这个采样点的量化误差。

当AD位数越高时，量化电平间隔会越小，因此，量化误差会越小，转化后的幅值精度越高。理想的模数转换器，量化误差均匀分布于（-1/2量化量级）～（+1/2量化量级）之间，如理想的24位AD，其量化误差分布于-0.6～+0.6μV之间。对于理想的M位AD而言，信号与量化噪声之比（SQNR）（或称为动态范围）可由下式计算：(www.xing528.com)

SQNR=20lg2^M=6.02MdB

由上式可以明白，1位AD，对应的动态范围为6.02dB。可以这样理解，由于每一位只能存储0或1，对应的数字大小为1=2⁰和2=2¹，相差2倍。我们知道，线性2倍，对应6dB。因此，1位AD对应的动态范围为6dB，常见AD位数，对应的SQNR见表2-2。

表2-2 不同位数的SQNR