声强测量的原理与方法

声强测量的基本方法是在空间一点同时测量平均声压和质点速度，然后把它们相乘并对时间求平均。当用声压梯度法测量质点速度时，测量两点声压后用积分方法从声压梯度中导出质点速度

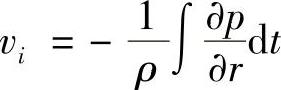
式中 ρ——空气密度。

当两个传声器的距离（隔离柱的长度）Δr小于被测声波最高频率分量的波长时，可以用差分替代微分。因此，在声波传播方向上的声压梯度可以用两个相距较小的传声器的声压差来近似

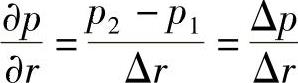
将上式代入质点速度公式，得

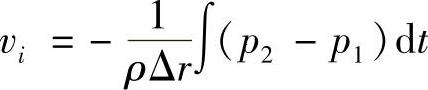
P-P探头结构如图1-69所示，由1#和2#传声器测量得到的声压分别为p₁和p₂，如果Δr<<λ，两个传声器连线中心处的声压近似值p和质点振动速度沿两个传声器连线方向的近似值v_i都可以用p₁和p₂来表示：

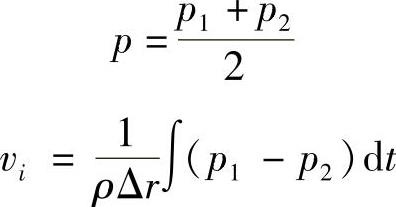
则声强沿两个传声器连线方向的近似值为

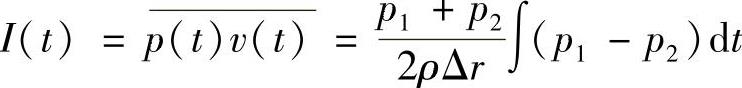
以上是声强的时域表达形式，实际上，也可以建立频域表达式。频域采用的是声压互谱来计算：

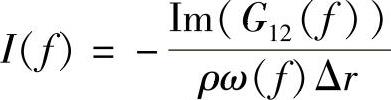
式中 G₁₂——声压p₁和p₂的互谱；

Im（G₁₂（f））——G₁₂的虚部；(www.xing528.com)

ω（f）——圆频率。

从声强的测量原理可知，在进行声强测试时，除了可以得到声强级，还可得到声压级。通过声压梯度来计算质点速度，可以用差分代替微分，但这是有频率限制的，正是这个

限制条件才导致声强测量时使用不同的隔离柱对应不同的频率范围。对于上限频率而言，如果隔离柱的长度远大于声波的波长，那么

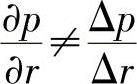
也就是说声音的频率很高，因而波长太短，导致声强计算出现明显的误差。如图1-73所示，如果声波的频率太高，必然导致差分代替微分的误差加大。对于精度要求在1dB以内，则要求

λ>6Δr如果满足这个条件，可以忽略高频误差。若隔离柱取12mm，即Δr=12mm，按上式求出来的频率上限为4778Hz（声速取344m/s）。如果Δr=λ/6，那么，通常隔离柱的相位变化为60°，相位误差在±0.3°，因而相位误差不明显。

图1-73 声强测量的上限频率

对于下限频率而言，主要考虑的是相位匹配。声波通过隔离柱时的相位改变量为

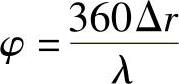
从上式可以看出，在低频段，频率越小，波长越长，而通过隔离柱的声波的相位变化将变小，如图1-74所示。例如，f=63Hz，λ=5.5m，Δr=12mm，相位变化等于0.8°。在这个例子中，声强测试将有明显的误差。如果隔离柱越长，如Δr=50mm，相位改变等于3.3°，声强测量结果将更精确。

我们知道，P-P探头由两个精选的相位匹配的传声器组成，理论上要求二者的相位差为0，但实际上二者还存在相位差，因此，声波通过隔离柱的相位改变量越小，误差越大，也即是低频声强测量需要使用更长的隔离柱，获得的相位改变更大，测量结果越精确。

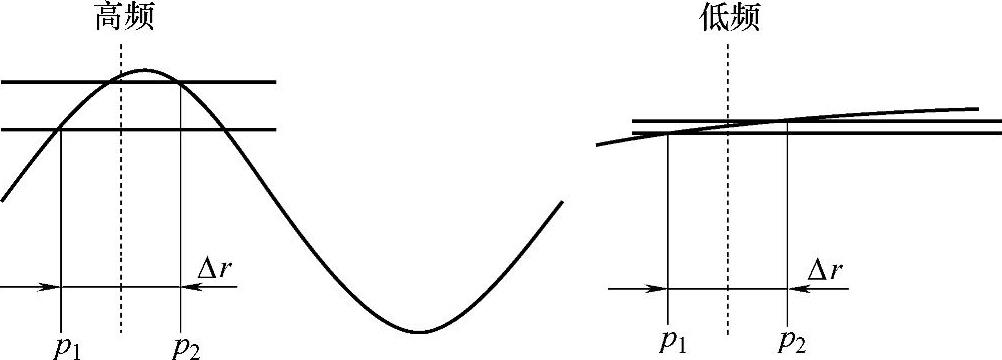
图1-74 声强测量的下限频率