声压级的定义与计算

通过前文1.1什么是声波的介绍，我们已经明白波动的声压是叠加在大气压之上的，但相较于大气静压强，声压的幅值波动非常小。如大气静压强为1.01325×10⁵Pa，而人耳可听的声压的幅值波动区间只有20μPa～20Pa，人们常处的声压环境和感受如图1-24所示，可以看出声压的幅值波动非常小。如教室内的声压值只有0.0063Pa，车内的声压值也只有0.063Pa，即使重型货车发出的声压值也只有0.63Pa。这些现实世界中的声压波动值远远小于大气静压强。

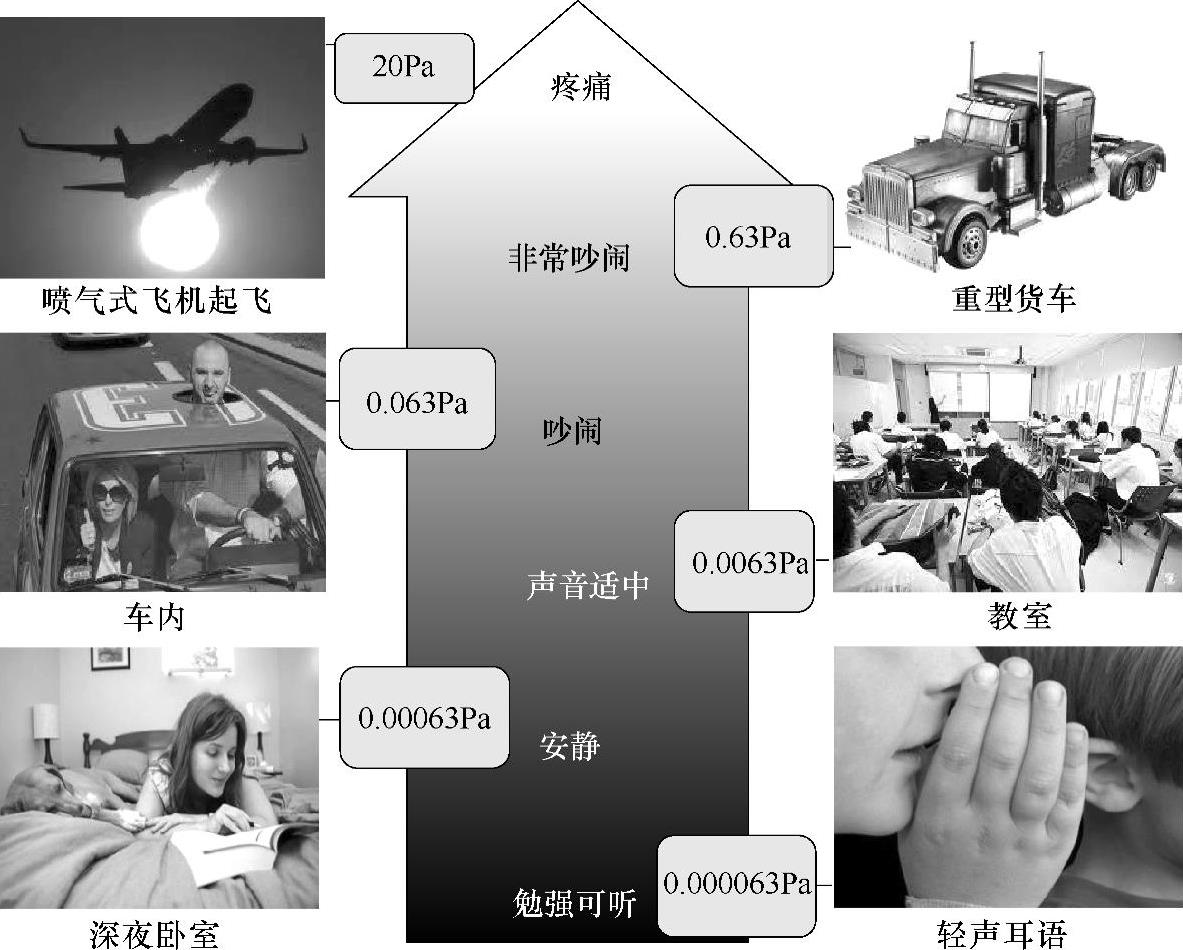
图1-24 常见各种声学环境下的声压值

在讲述声压级之前，我们先对比一下线性尺度和分贝尺度。如图1-25a所示为线性尺度，对应的声压分别为1Pa和0.001Pa，二者相差了1000倍。图1-25b所示为这两个线性声压的分贝表示形式（基准为1），对应的分贝分别为0dB和-60dB。可以看出，在线性尺度下，相比较1Pa的声压，0.001Pa的声压幅值几乎看不出来，但在分贝尺度下，0.001Pa的分贝值仍较高。也就是说，在分贝尺度下，更易于对比变化巨大的线性幅值。从图1-25中可以看出，线性幅值相差1000倍，分贝值只相差60dB。

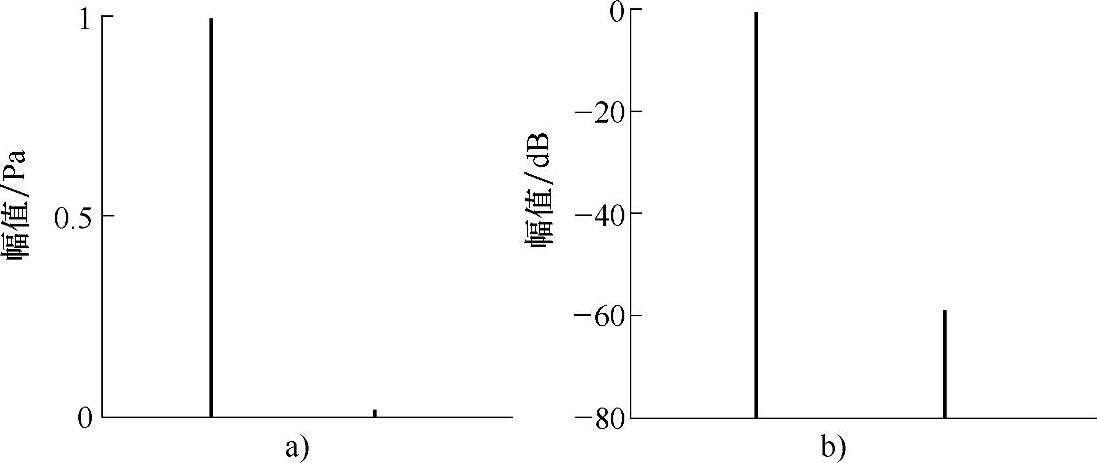
图1-25 不同尺度下的幅值

a）线性尺度 b）分贝尺度

从另一方面来讲，人的大脑对瞬时声压幅值波动没有响应，但对动态声压的均方根值（RMS）有响应，平均响应时间间隔约为35ms。时间T内的声压的均方根值计算如下：

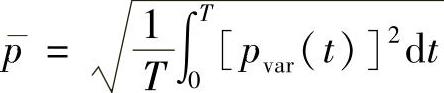
式中，p_var为波动的声压瞬时幅值。注意，由上式计算出来的均方根值不等于瞬时声压幅值。对于一个纯音而言，均方根值等于其幅值的0.707倍。(www.xing528.com)

人耳听觉系统也近似是对数尺度，因此，引入了以dB形式定义的声压级

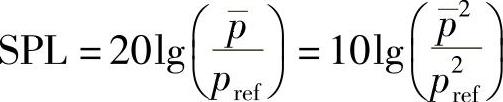
式中，p_ref表示1000Hz处人耳可听的最小声压幅值20μPa。上式中声压级计算所用的声压p一定是声压的均方根值，或者是声压的均方值（如果采用10倍的对数形式）。在传声器校准时，常用94dB和114dB，对应的声压有效值分别为1Pa和10Pa，见表1-4。

表1-4 常见声压级、声压有效值及作用

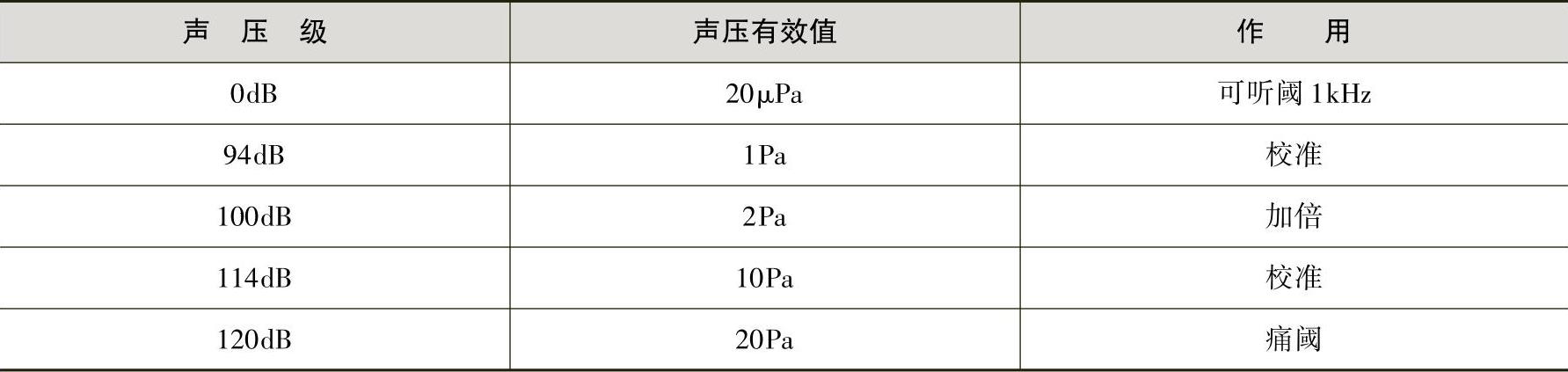
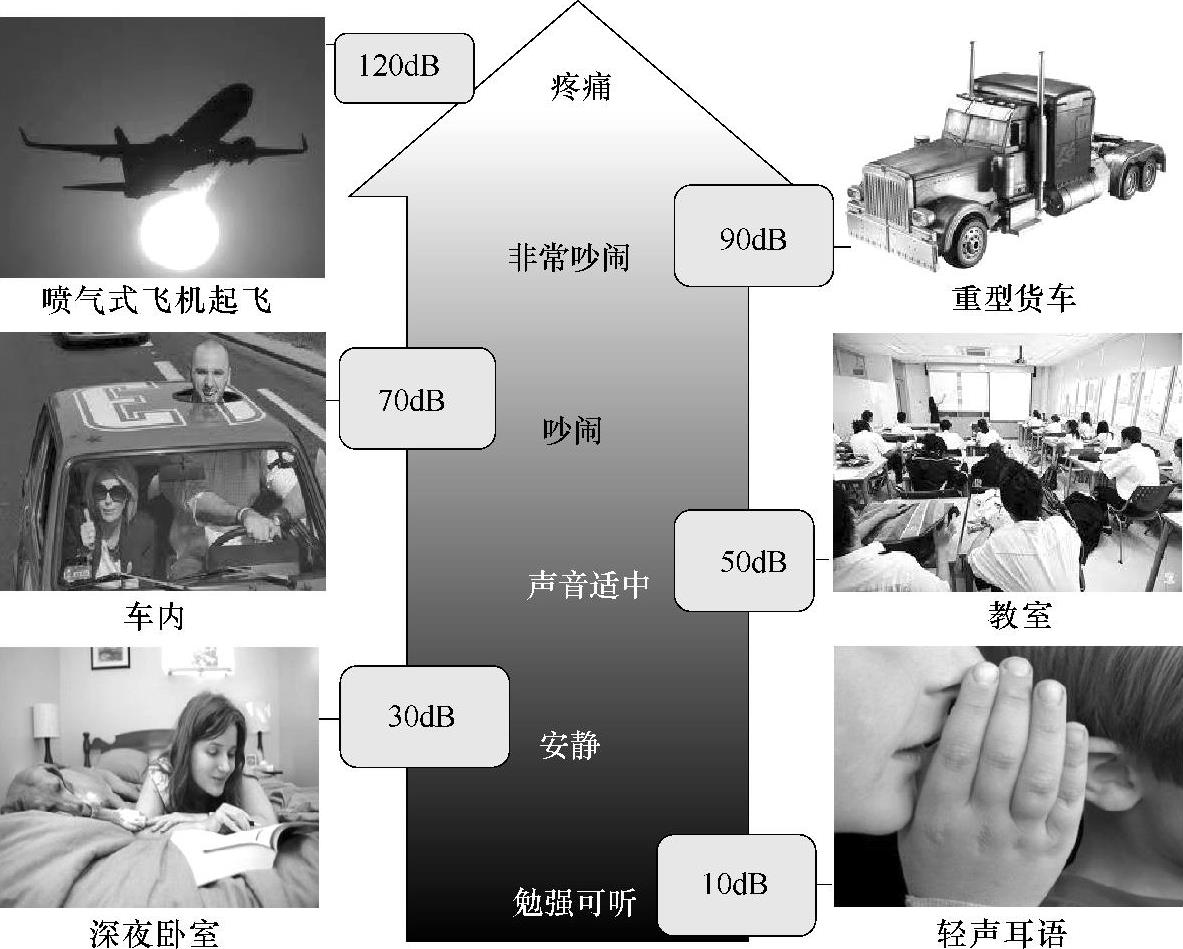
图1-26 常见各种声学环境下的声压级

声压级常用符号SPL来表示，但也有用其他符号，如L_p、L、LdB，L（dB）或L（dBA）等形式，A表示A计权。将前面用声压表示的声学环境采用声压级来表示，则如图1-26所示。从这两幅图中也可以看出线性声压变化关系在dB中的变化幅度，关于更多dB知识，请参考本章1.5什么是分贝dB。