声波描述参数简述

相应于振动，声波也分为周期性声波和非周期性声波，最简单的周期声波是单频的声波，

也称为纯音。它是由简谐振动产生的频率固定、并按正弦变化的声波。与单频音相对应的是

复合声，复合声（也称为复声）是由一些频率不同的单频音组成的，由傅里叶变换（FFT）

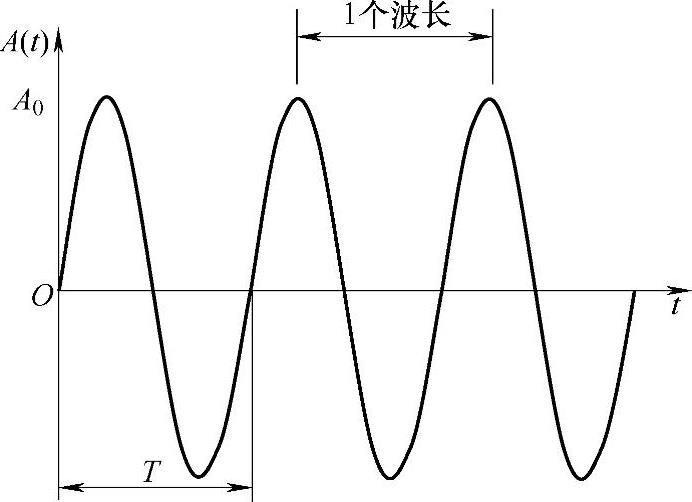
可知，可将任何复声分解为一系列单频音。集中质量-弹簧模型的振动形式为简谐振动，其运动方程为正弦表达形式。同样，单频声波（见图1-4）也可以用这个函数来表示，即

A（t）A₀sin（2πft+θ）

式中 A₀——振动幅值；

f——每秒的循环次数，也等于1/T，T为完

成一个振动循环所需要的时间；

θ——初相位。

对于声波而言，除了以上参数之外，还有另外两个参数：波长和波数。波长是指周期声波中相邻的等声压点之间的距离，通常用λ表示。波长等于声速c与声波频率f之比，也等于声速c与周期T之积，即

(www.xing528.com)

图1-4 单频声波的定义

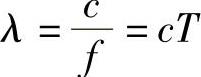
也即是波长等于声波在一个周期内传播的距离，如图1-4所示。从上式可以看出，由于空气中的声速是确定的，因而，声波频率越高，波长越短。低频声波波长长，高频声波波长短。

波数是指2π弧度内波长的个数，因为正弦（或余弦）函数是周期函数，每增加2π弧度，函数值就重复，因此，有

k=2π/λ

而λ=c/f，代入上式，得到波数k的另一种表示形式

k=ω/c

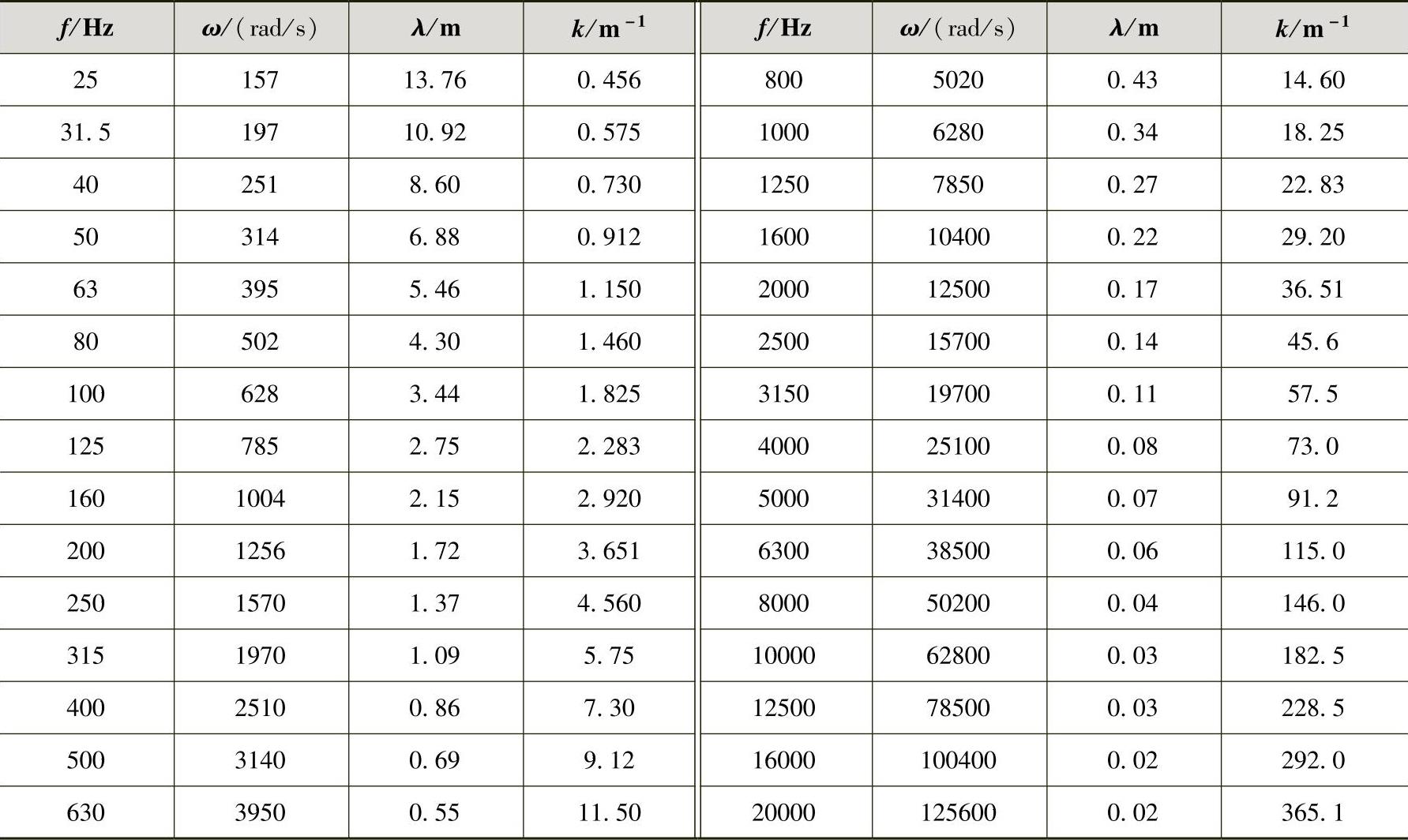
给定频率下的圆频率、波长与波数见表1-2，此时取空气中的声速为344m/s。

表1-2 给定频率下的圆频率、波长与波数