【摘要】:计算法是对虾米腰直角弯头的形状特点进行分析,归纳出一套求表面实形所有邻边线段实长的公式,由它的已知条件求出这些邻边线段的实长,并用这些实长来画展开图。用以上公式可以计算出各等分线上的高Hi、圆管展开全长S、圆管每等分展开长度L、虾米腰小节内侧高度H、虾米腰小节外侧高度H1。这种方法随着袖珍计算器的普及,日益被人们重视和应用。
计算法是对虾米腰直角弯头的形状特点进行分析,归纳出一套求表面实形所有邻边线段实长的公式,由它的已知条件求出这些邻边线段的实长,并用这些实长来画展开图。
图1-2是虾米腰直角弯头的数学模型。
已知:n、n1、d、r,i=1,2,…,n。
求:Hi、S、L、H、H1。
n——等分数,它和圆管直径大小成正比,一般取8、12、16、24、32等。
n1——虾米腰口数,虾米腰节之间的连接数,即虾米腰节数减一;
d——圆管直径,可以是内径、中径、外径等;
r——弯曲半径,即虾米腰中心半径;
Hi——各等分线号上的高度;
S——圆管展开全长;
L——圆管每等分展开长度;
H——虾米腰小节内侧高度;(https://www.xing528.com)
H1——虾米腰小节外侧高度。
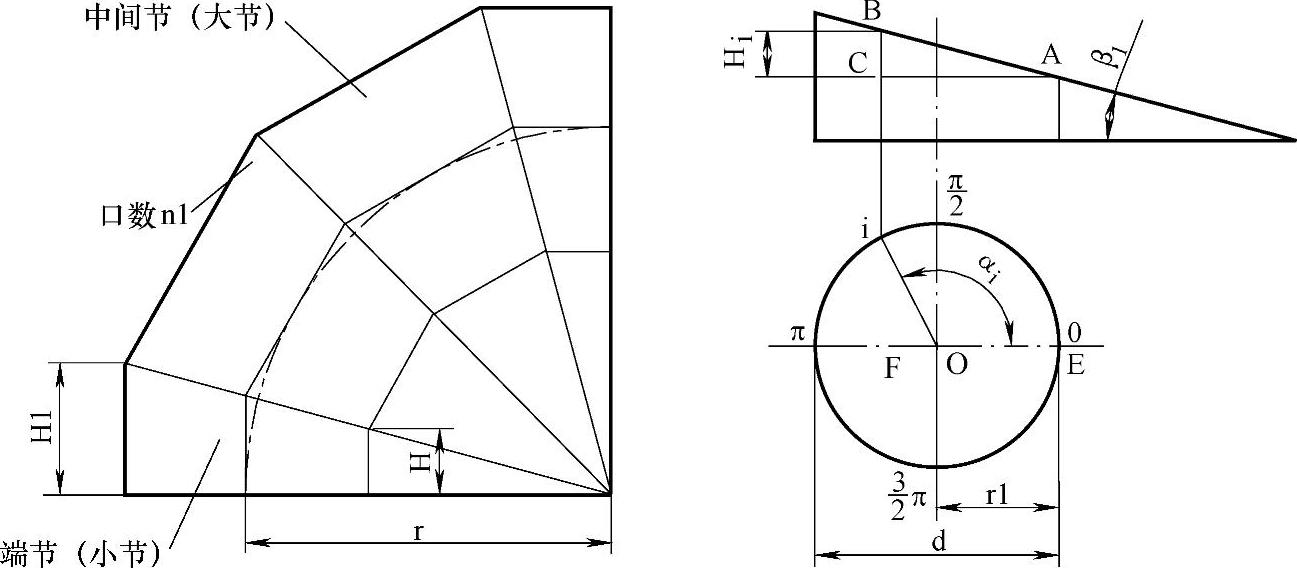
图1-2
解:因为
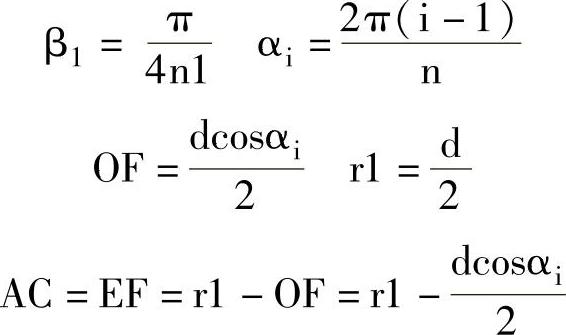
所以

假如口数为3、等分数为12,式(1-1)就可以演算成以下求各等分高(实长)公式。

用以上公式可以计算出各等分线上的高Hi、圆管展开全长S、圆管每等分展开长度L、虾米腰小节内侧高度H、虾米腰小节外侧高度H1。使用这些数据可以直接在圆管上展开放样。目前有不少书籍已经总结推导出各种情况的公式,作业人员不需自行推导公式,直接使用即可。这种方法随着袖珍计算器的普及,日益被人们重视和应用。因此这种方法不仅减少了劳动强度,而且可节约施工现场放大样所花费的时间。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




