FDM-GRA方案的评价方法

1.FDM-GRA总体流程

GRA在计算灰色关联度时,可为各个评价指标赋予不同的权重。虽然GRA本身并没有提供相应的赋权方法,但是这项权重系数的存在却可以起到接口的功能,为GRA与其他方法的融合提供了可能,从而提高整体评价性能。因此,本书提出的FDM-GRA方案评价方法同样以指标权重的方式实现FDM与GRA的融合,即将FDM所得到的各个评价指标的全局权重作为灰色关联度计算中的指标权重,从而建立FDM-GRA方案评价方法的总体流程,如图6.9所示。

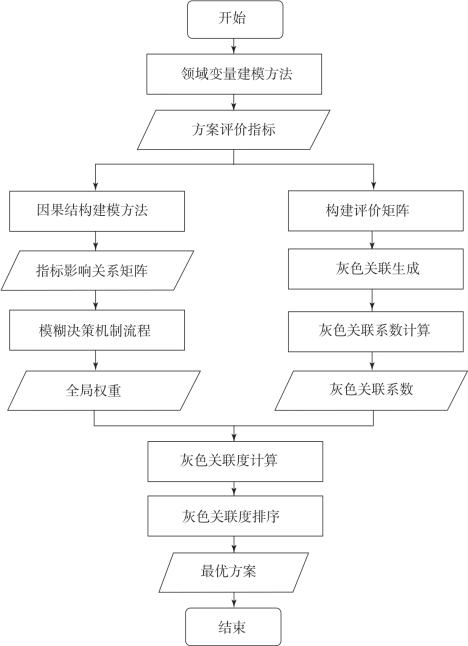
图6.9　FDM-GRA方案评价方法总体流程

该方案评价方法以模糊决策机制(FDM)作为赋权方法来表达评价指标之间的综合影响关系,以灰色关联分析(GRA)作为方案评价主体方法对备选方案进行评价,最后根据计算出的各备选方案的灰色关联度的排序确定最优方案,实现了模糊决策机制与灰色关联分析的优势互补,从而形成了一套完整的、可以表达评价指标之间综合影响关系的方案评价方法。

2.FDM-GRA具体步骤

基于FDM-GRA的方案评价方法总体流程嵌入了领域变量建模方法、因果结构建模方法和模糊决策机制流程,并融合了灰色关联分析的方法流程。本节详细阐述方案评价过程。

步骤1:确定方案评价指标。

针对具体问题确定方案评价的总目标及各项评价指标,详细流程可参见6.2.2节领域变量的建模方法。设针对某一具体方案评价问题,总目标为“选择××综合最优设计方案”;共有n个评价指标,则该方案评价问题的评价指标向量为

Y=[y1,y2,…,yj,…,yn]

式中,yj代表第j个评价指标。

步骤2:构建模糊认知图。

请领域专家对方案评价指标之间的影响关系进行判断和确定,并为影响关系赋权,得到方案评价指标的模糊认知图,详细流程可参见6.2.2节因果结构的建模方法。

其中,方案评价体系中的j个评价指标作为模糊认知图的j个节点。若专家认为某两个评价指标存在关联,则为代表这两个评价指标的节点连线,表示两者相互影响,并为该连线赋予一定的权重,以表达相互影响的程度。该影响关系权重可用定量化的数值[-1,1]来表达。其中正数代表两个评价指标正相关,即一个评价指标增大或减小会导致另一个评价指标增大或减小;负数代表负相关,即一个评价指标增大或减小会导致另一个评价指标减小或增大。数值的绝对值越大,即越接近1或者-1,代表两个评价指标间的影响程度越高。

步骤3:将影响关系转换为影响矩阵E。

根据步骤2所得的指标影响关系模糊认知图将评价指标间的影响关系转换为影响矩阵E:

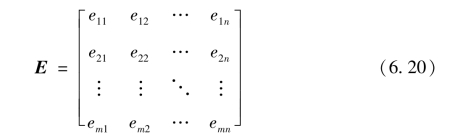
式中,eik代表评价指标yj对评价指标yk的影响,eik∈[-1,1];特殊地,当j=k时,ejj=0。

步骤4:构建局部权重的判断矩阵Z。

在步骤1所确定的方案评价指标的基础上,请设计人员两两比较每个评价指标对于总目标的重要程度,得到局部权重的判断矩阵Z:

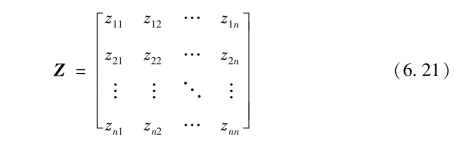
式中,zjk代表评价指标yi相对于评价指标yk对于总目标的重要程度,且zjj=1,zjk与zkj的值互为倒数。

具体评分可采用“五分制”方法,即评分集合为[1,2,3,4,5],评分越高,则代表越重要。例如,如果zjk=2,则代表当评价指标yj与评价指标yk相互比较时,评价指标yj对于总目标会更加重要一些,同时也就意味着(www.xing528.com)

步骤5:计算局部权重。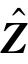

利用求矩阵特征向量的方法,计算局部权重判断矩阵的特征向量,并对结果进行一致性检验,若检验通过,则此特征向量中的每一个值zj即评价指标yj的局部权重。具体方法参见6.3.1节。

步骤6:通过迭代运算得到全局权重W。

步骤3中的影响矩阵E只是对评价指标两两之间的直接影响关系进行了表达,并不能表达出评价指标之间的综合影响关系。而此步骤的目的正是利用模糊认知图(FCM)关于迭代运算的理论,计算出各个评价指标在两两相互影响的基础上,通过影响的传递性作用而最终形成的综合影响关系。

迭代运算以局部权重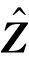作为初始迭代向量,即C(0)=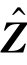,取阈值函数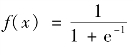,根据迭代公式(6.2)进行迭代运算。当系统达到最终状态,得到输出向量。对输出向量进行归一化处理,得到全局权重W。

步骤7:构建评价矩阵。

设有m个备选方案。根据方案评价指标,请评价人员为每一个备选方案进行打分。如果是定量指标,则评分为具体的数值;如果是定性指标,则可根据1~10的评分等级为备选方案评分,分值越高代表该备选方案在此评价指标下的表现越好。从而建立指标矩阵X:

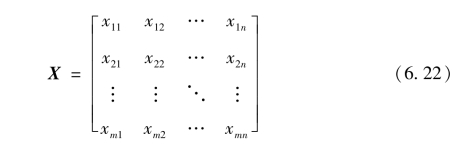
式中,xij表示第i个备选方案在第j个评价指标下的评价值。

步骤8:灰色关联生成。

在指标矩阵的基础上,考虑各个评价指标的极性,对指标矩阵进行等极化与归一化处理,从而得到决策矩阵。等极化处理的目的是将所有评价指标统一变成极大型指标以利于相互比较,归一化处理的目的是将所有评价值标准化处理为[0,1]的数值。等极化处理与归一化处理统称为灰色关联生成。经过灰色关联生成后,各备选方案在各评价指标下的表现优劣可以直接通过比较其评价值的大小来判断。详细流程和公式可参见6.3.2节。

经过等极化处理后得到的矩阵称为等极化矩阵:

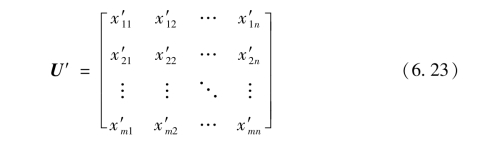
对等极化矩阵进行归一化处理后得到决策矩阵:

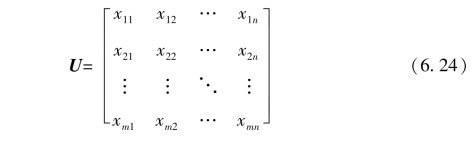
步骤9:灰色关联系数计算。

灰色关联系数的本质是以数值的形式表达各备选方案在各项评价指标下的评价值与最优参考值1之间的距离,以模拟评价数据序列的几何关系与参考曲线之间的相似程度。曲线间的相似程度越大,则证明关联度越大,备选方案越优。因此,其运算结果是决定后续灰色关联度计算的基础。详细流程和公式参见6.3.2节灰色关联分析介绍。

步骤10:灰色关联度计算。

在全局权重及灰色关联系数的共同基础上,利用灰色关联度计算公式计算出各项备选方案的灰色关联度R。

步骤11:获取最优方案。

将各项备选方案的灰色关联度按数值大小进行排序,数值最大者为最优方案。同时,如果某一备选方案的灰色关联度与最优方案的灰色关联度极为接近,按照情理应该也可被列为值得推荐的优秀方案。因此,这里设定一个“最优方案差异系数”D。

式中,Dj代表第j个备选方案的最优方案差异系数,rj代表第j个备选方案的灰色关联度,rmax代表各备选方案中的最大灰色关联度,即最优方案的灰色关联度。若D＜0.01,则认为此方案与最优方案之间并无重大区别,可被列为值得推荐的优秀方案。