模糊决策机制的应用及优化方法

1.模糊决策的基本思路

图6.6　全局指标权重的推理

模糊决策机制的构建依托于模糊认知图理论中的推理迭代机制。由6.2.1节的介绍可知,模糊认知图的推理迭代机制可以概括为:输入一个初始状态向量,在影响矩阵的作用下,通过若干次迭代,得到一个输出向量。结合方案评价的背景,通过类比可以建立模糊决策机制,如图6.6所示。因此,模糊决策机制的基本思想是:首先通过某种手段获得指标重要程度初始表达向量,该向量的元素个数等于方案评价指标总数,各个元素分别代表指标的权重,各元素之和为1。然后,将这个向量作为初始状态向量,将模糊认知图模型表的指标影响关系作为影响矩阵,代入模糊认知图的迭代公式中进行推理。这个推理过程的实际含义是:初步表达指标重要程度的向量在影响矩阵的作用下,会因为影响关系的传递而不断发生变化,当整个系统达到稳定模式时,就意味着各个指标的重要程度已经在错综复杂的彼此影响作用之后重新达到平衡状态。那么,此时的输出向量就可以作为最终所需要的指标权重,因为它已经代表了指标之间的综合影响关系。

定义1　局部权重

在未考虑评价指标之间的相互影响时,每一个评价指标的重要程度用z来表示。

定义2　全局权重

在考虑评价指标之间的综合影响关系后,每一个评价指标的重要程度用w来表示。

图6.6中的“可以初步表达指标重要程度的向量”即局部权重,最终所要获得的指标权重即全局权重。

2.模糊决策的运行过程

局部权重的获取方法采用单层次分析法,即以评价目标作为目标层的总目标,如“选择×××设计方案”;以各个方案评价指标作为准则层,构成总目标下的单层次结构,如图6.7所示。然后根据层次分析法的相关方法计算局部权重,具体流程如下:

(1)采用“成对比较法”请专家两两判断各评价指标相对于总目标的重要程度,构成局部权重的判断矩阵。判断值的大小可采取五分位比率,即取值为1,2,3,4,5及相应的倒数1,1/2,1/3,1/4,1/5。

(2)计算判断矩阵的最大特征值λ和特征向量A。

图6.7　局部权重的单层次结构(www.xing528.com)

(3)对计算结果进行一致性检验。

(4)若通过一致性检验,则对特征向量进行归一化处理得到局部权重;否则请专家重新建立判断矩阵。

一致性检验分为三个步骤,具体如下:

(1)计算一致性指标CI,计算公式为

式中,λ为判断矩阵的最大特征值;n为评价指标的个数。

(2)确定随机一致性指标RI,RI的取值根据n值的不同而不同,可从表6.3中查得。

表6.3　RI取值

(3)计算一致性比率CR,用于确定判断矩阵不一致程度的容许范围,公式如下:

当CR＜0.1时,表示判断矩阵的不一致性程度在容许范围内,可用判断矩阵的特征向量作为局部权重向量。

得到局部权重向量后,利用式(6.2)进行迭代推理。当系统达到最终模式时,对输出向量进行归一化处理,即可得到全局权重。该全局权重就是可以与灰色关联分析相结合的指标权重。综上所述,模糊决策机制的整体流程如图6.8所示。

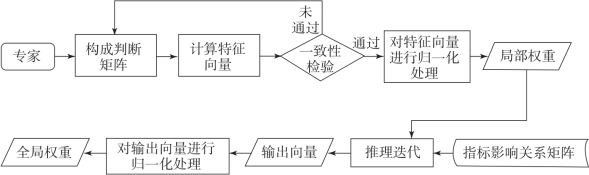
图6.8　模糊决策机制整体流程