数值型指标的相似度计算方法优化

数值型指标是需求信息中最常见的指标表达形式,通常是对某一指标的定量化描述,数值型指标通常有一定的变化范围。本书在已有数值型参数相似度计算方法的基础上,提出了改进的计算方法,其相似度计算如式(5.1)所示。

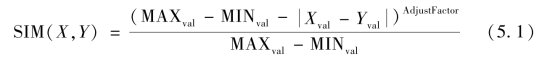
式中,X,Y表示同一数值型指标;MAXval,MINval分别为X、Y取值范围的上下限;Xval,Yval分别为X、Y的具体取值;AdjustFactor为调整系数,其值由式(5.2)计算得到。引入调整系数后可以显著地增大数值型指标在微小差异情况下的相似度差异,能够较好地区分相似案例。图5.1所示为引入调整系数AdjustFactor前后的相似度对比图。

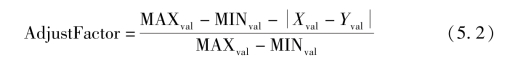(www.xing528.com)

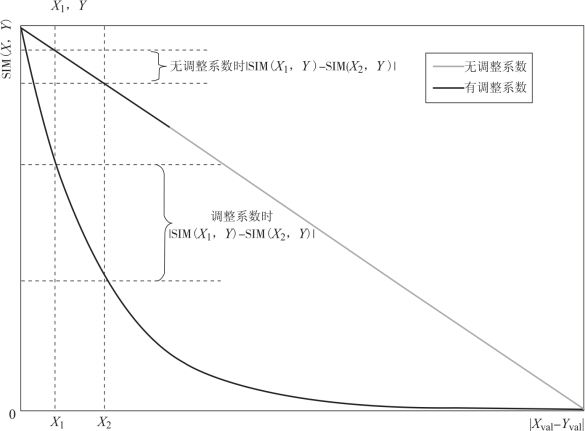
图5.1　引入AdjustFactor前后数值型指标相似度对比图

举例说明,口径7~15 mm的枪械,其理论射速范围为400~1 100发/min。知识库中的两案例理论射速分别为700发/min和750发/min。若当前需求指标理论射速为800发/min,则没有调整系数情况下两者相似度差异约为0.072,引入调整系数后两者相似度差异约为0.243;若当前需求指标理论射速为500发/min,则没有调整系数情况下两者相似度差异约为0.071,引入调整系数后两者相似度差异约为0.009 5。可以看到,当案例理论射速与当前需求接近时,调整系数放大了数值型指标的差异,提高了案例选择的区分度;而当案例理论射速与当前需求差距较大时,虽然缩小了指标相似度差异,但其相似度本身亦很小,对总体相似度的影响甚微。