光伏发电并网的结构及控制技术

光伏发电系统的运行方式分为独立光伏发电系统和并网光伏发电系统两种。独立光伏发电系统直接给负载供电，不与电网联网，而并网光伏发电系统接入电网中，光伏电源与电网一起向网络中的负载供电。

根据有无隔离变压器，并网光伏发电系统分为隔离型和非隔离型两大类，隔离型并网光伏发电系统可以避免直流电流注入电网中，但隔离变压器的损耗降低了光伏发电系统的效率。在不需要强制电气隔离的条件下，可以采用无隔离变压器的光伏换流器，它具有体积小、效率高、成本低的优点。

非隔离型光伏换流器常有双级变换结构和单级换流结构两种。双极换流结构由DC-DC换流器和DC-AC逆变器两级换流器组成，单级结构则仅有DC-AC逆变器。无论何种结构形式并网，控制功能都包括最大功率点跟踪控制、电网电流控制和直流母线电压控制。

6.2.3.1 双级换流结构

图6-8给出了两级式光伏发电并网的主电路及控制电路。前级DC-DC换流器通常采用Boost电路，以便为后级逆变器提供所需的电压，其控制目标是实现MPPT。后级并网逆变器通常采用两电平或三电平电压源换流器，其控制目标为稳定直流母线电压，一方面维持电压源换流器的直流电压水平，另一方面实现前后级的功率随动平衡。这种控制方式下，前级与后级在控制上是相互独立的。

（1）前级升压控制

如图6-8所示，Boost电路由储能电感L₁、二极管VD₂和直流滤波电容器C_dc组成，并且假设电容C_dc和电感L₁足够大。当开关管VI₀开通时，设开通时间为t_on，光伏电池以基本恒定的电流I_L使L₁储存磁能，电容C_dc上的电压U_dc基本恒定，并向逆变器供电，此过程中，电感L₁储存的能量为U_PVI_Lt_on；当开关管VI₀关断时，设关断时间为t_off，光伏电池和电感L₁同时向电容C_dc充电，并且向逆变器提供能量，此过程中，电感L₁上释放的能量为(U_dc-U_pv)I_Lt_off。根据能量守恒定律，当Boost电路处于稳态时，在一个开关周期内，电感L₁上释放的能量和储存的能量相等，即

U_PVI_Lt_on＝(U_dc-U_PV)I_Lt_off

于是可得

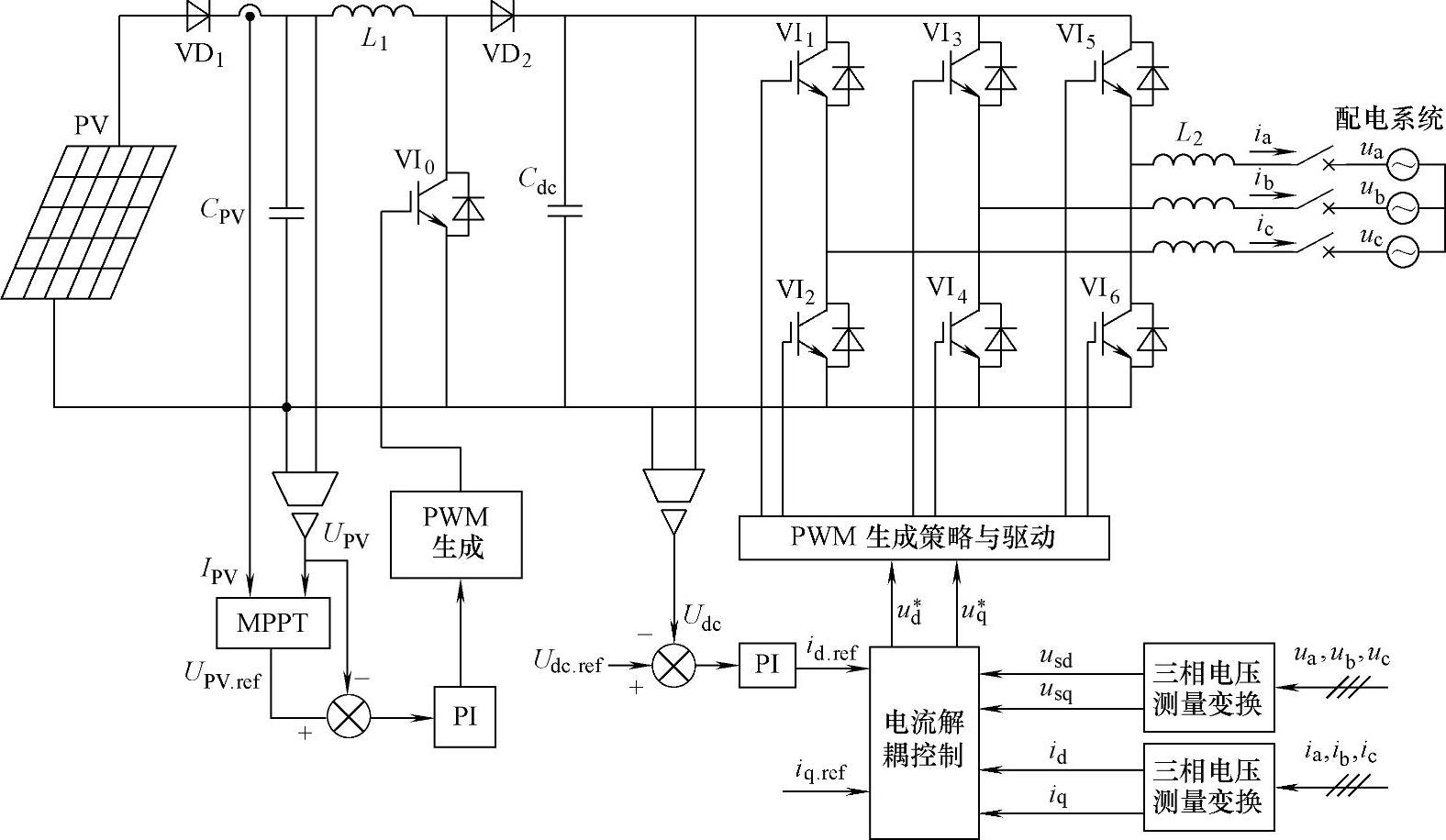
图6-8 两级式光伏发电并网的主电路及控制电路框图

式中 d——占空比。

显然，通过控制占空比d就可以控制Boost电路的输出电压。设开关周期为T_s，则

d＝t_on/（t_on＋t_off）＝t_on/T_s

前级DC-DC换流器的MPPT控制策略如图6-8所示，通过采集光伏电池阵列输出的电压和电流，进行最大功率点跟踪，可得到光伏输出参考电压U_PV.ref，与电池实际输出电压U_PV比较后，经PI调节器控制Boost电路开关占空比。这里因为直流母线电压稳定是由后级控制的，那么调节Boost电路占空比相当于调节光伏输出电流，实现光伏功率的最大化输出。

根据增量电导法，如果功率跟踪搜索运行在光伏电池P-U曲线的左侧，则令sgn（ΔP_PV/ΔU_PV）＝1；运行在曲线的右侧时，令sgn（ΔP_PV/ΔU_PV）＝-1；运行在最大功率点处时，令sgn（ΔP_PV/ΔU_PV）＝0。于是，基于电导增量法的最大功率点跟踪算法可表示如下：

U_PV.ref［n＋1］＝U_PV.ref［n］＋sgn（ΔP_PV/ΔU_PV）ΔU

因此，基于Boost电路的电导增量法最大功率点跟踪控制系统框图如图6-9所示。

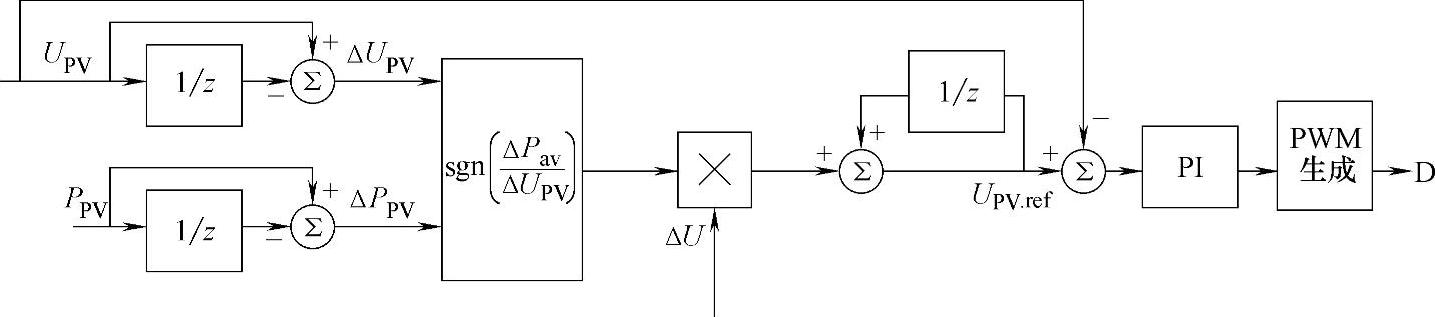
图6-9 基于Boost电路的电导增量法最大功率点跟踪控制

值得指出的是，如果Boost电路的电感L₁和开关频率配合不当，在VI₀导通状态下，光伏电池阵列的输出电流和电压可能变化较大，引起输出功率的波动，导致输出功率偏离最大功率点。此外，光伏系统设计中要协调选择光伏电池阵列开路电压和逆变器直流母线电压，使得Boost电路的升压比在2～3之间、开关器件占空比在30％～80％之间为宜。如果占空比D大于80％，由于电流限制和实际电路的各种非理想因素，Boost电路的升压比可能随D的增大而不升反降。

（2）后级逆变控制

如图6-8所示，后级逆变并网换流器是一个典型的两电平电压源换流器，主电路由IGBT（VI₁～VI₆）、直流滤波电容器C_dc和交流串联电抗器L₂组成。实际上，直流滤波电容器C_dc是前级Boost电路与后级逆变并网电路共用的，也起到两级换流器独立控制的解耦作用。

设来自光伏电池的功率为P_PV，逆变并网的功率为P_inv，若忽略换流器的损耗，则两级不平衡功率注入到直流电容器中，即

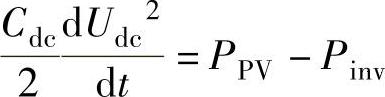
因此，如果保持直流母线电压稳定，则实现了两级功率平衡和最大功率点跟踪控制。如果P_PV＞P_inv，则直流滤波电容器充电，直流电压升高；如果P_PV＜P_inv，则直流滤波电容器放电，直流电压降低。为了维持前后级能量平衡，后级逆变器常采用定直流母线电压控制来实现能量的传递和平衡。为了确保后级对光伏输出能量及时调整而不会在直流母线上容量发生不匹配，在控制系统设计时，后级逆变器的直流电压控制速度应快于前级Boost电路的MPPT控制。

在实际系统中，应实时检测直流母线电压是否超出电压允许范围。当外界光照强度很低，以至于前级Boost电路无法升压到直流母线电压运行下限值时，应当关闭光伏发电系统。

逆变并网控制一般要实现网侧单位功率因数电流并网控制，在某些情况下，可以根据需要增加无功补偿和有源滤波功能。

逆变器控制可以采用三相自然坐标系下的直接电流控制，或采用两相静止坐标系下比例谐振控制，或采用两相旋转坐标系下的dq电流解耦控制。下面着重说明三相自然坐标系下的直接电流控制，如图6-10所示。

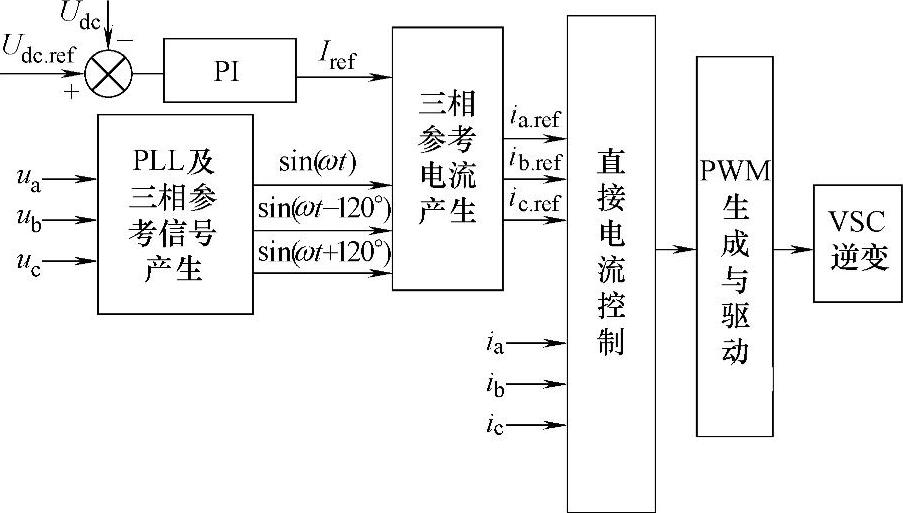
图6-10 三相自然坐标系下的直接电流控制

图6-10中，直流电压给定值U_dc.ref与直流电压采样值U_dc比较后，经过PI调节器，可以获得后级逆变并网参考电流幅值I_ref，电网电压经锁相环后得到三相参考电流的相位，电流幅值与相位合成产生三相参考电流。该参考电流与逆变器输出电流比较，经直接电流控制产生PWM信号。

直接电流控制可以采用滞环控制、三角波控制、定频控制、预测电流控制等方法来实现。其中，预测电流控制是一种基于电路模型的控制方法，其基本思想是根据本周期以前的采样值，用模型计算出要达到指定的状态和输出所需的方波脉冲宽度和极性，使输出电流值与下一时刻采样值相吻合。不断调整每一采样周期内方波脉冲的宽度和极性，就能使输出的实际电流波形接近于指令电流波形。该控制方法具有如下优点：暂态响应快，仅为数个开关周期，波形畸变率小，即使开关频率不是很高，也能得到较好的输出电流波形等。

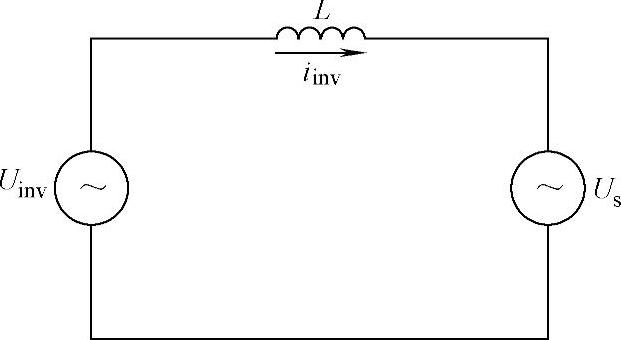
图6-11 并网逆变器等效电路

1）预测电流控制原理：图6-11是并网逆变器的等效电路。若忽略开关器件压降、串联电感上的寄生电阻和死区时间影响，逆变输出电压U_inv与电网电压U_s之间的关系可用下式来表示：

一般开关周期T_s较短，所以对于开关周期（k，k＋1）内，对式（6-4）进行离散化，可得

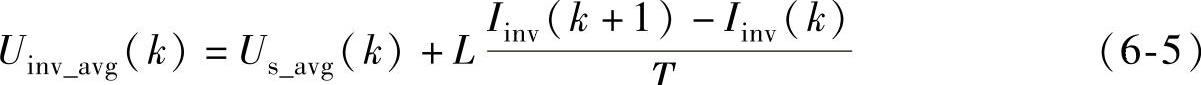
式中 U_{inv_avg}（k）、U_{s_avg}（k）——开关周期（k，k＋1）内逆变器的平均输出电压和电网的平均电压；

I_inv（k）、I_inv（k＋1）——逆变器在第k个开关周期和第k＋1个开关周期的输出电流。

假设在开关周期内，电网电压变化是线性的，并且第（k，k＋1）周期的电网电压变化等于第（k-1，k）开关周期的电网电压变化，则通过前2个开关周期所测得的电网电压可获得当前周期电网电压平均值U_{s_avg}（k），如下式所示：

U_{s_avg}（k）＝2.5U_s（k-1）-1.5U_s（k-2） （6-6）

在开关周期（k-1，k）中，I_inv（k）可用下式表示：

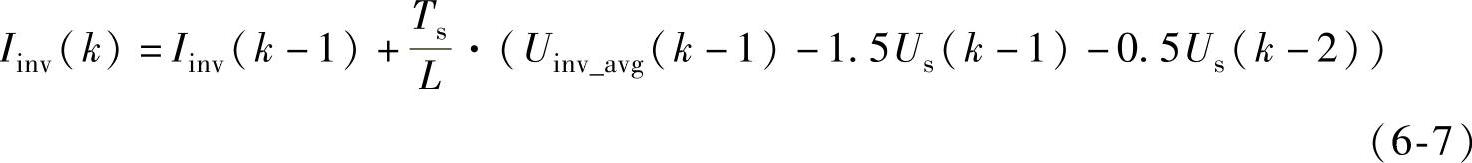
设I_inv（k＋1）＝I_ref（k＋1），根据式（6-6）和式（6-7），可得到式（6-8）。

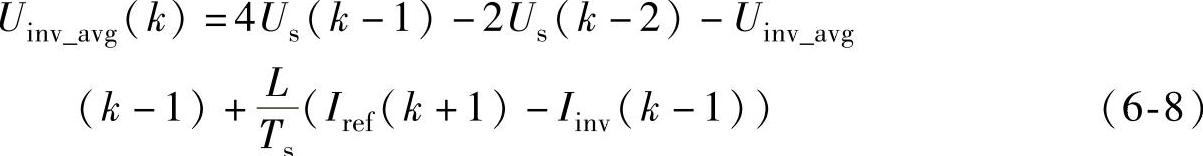
直流母线电压通过一阶惯性滤波环节滤波，用下式表示：

U_{dc_avg}（k）＝α·U_dc（k）＋（1-α）·U_{dc_avg}（k-1） （6-9）

式中 α——常数，且0＜α＜1。

调制系数m如下式所示：

(www.xing528.com)

由式（6-8）、式（6-9）和式（6-10）可以得到式（6-11）。

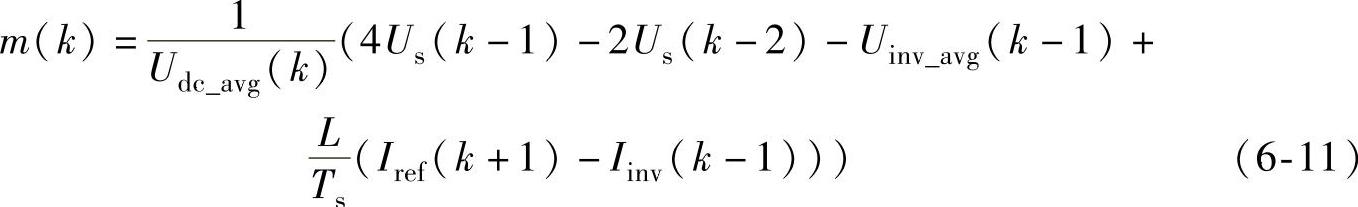
图6-12为两级式光伏发电并网系统仿真模型，图6-13给出相应的仿真结果。在1s时，光照从标准光照突变为1.2倍标准光照，此时直流母线能够稳定在800V左右，同时系统的光伏输出功率增加，逆变并网电流也增加，并具有单位功率因数并网功能。

2）串联电感变化引起的问题：假设直流母线电压恒定，电网电压正常，以及参考电流相位与电网电压相位一致。当实际电感等于标称电感L时，电感电压如式（6-12）所示。当实际电感变化时，电感电压如式（6-13）所示，由式（6-12）和式（6-13）可得出实际电感电压变化，如式（6-14）所示。

图6-12 两级式光伏发电并网系统仿真模型

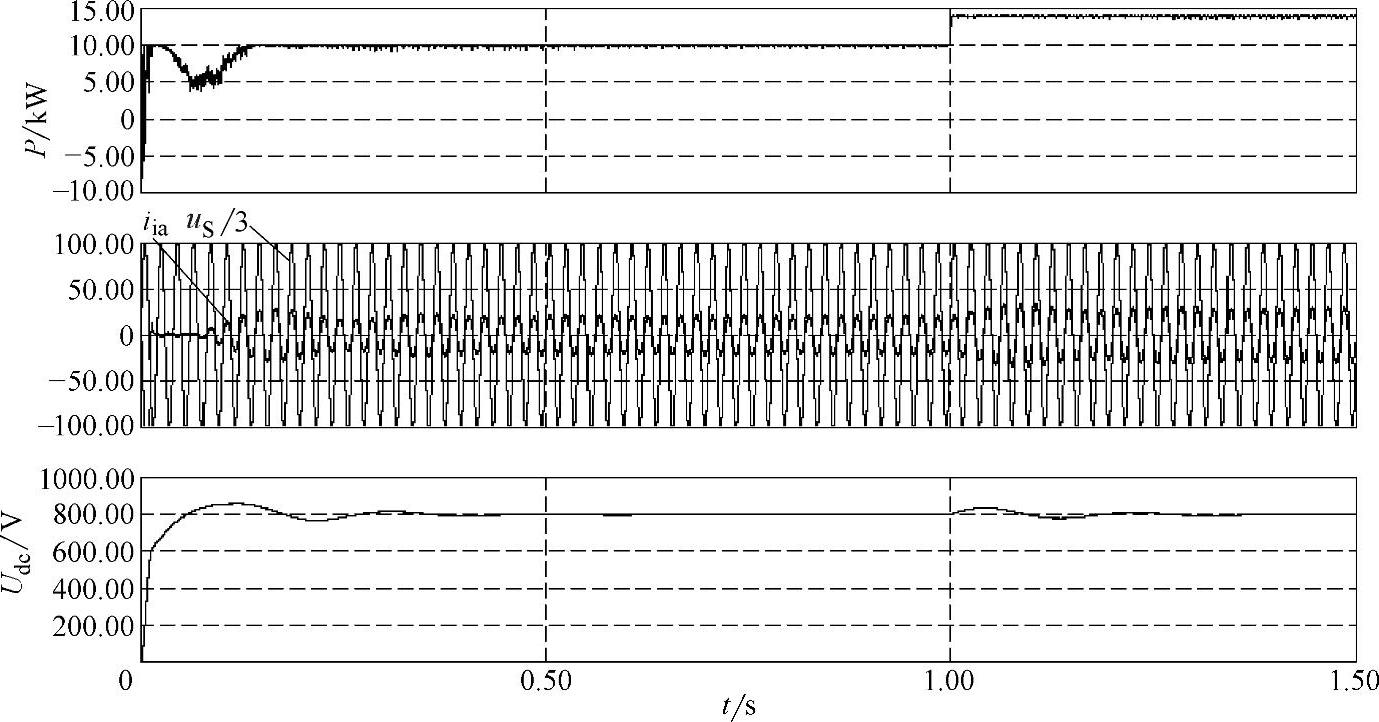
图6-13 光照突变时光伏发电并网系统输出功率以及交流侧并网电流和电压仿真波形

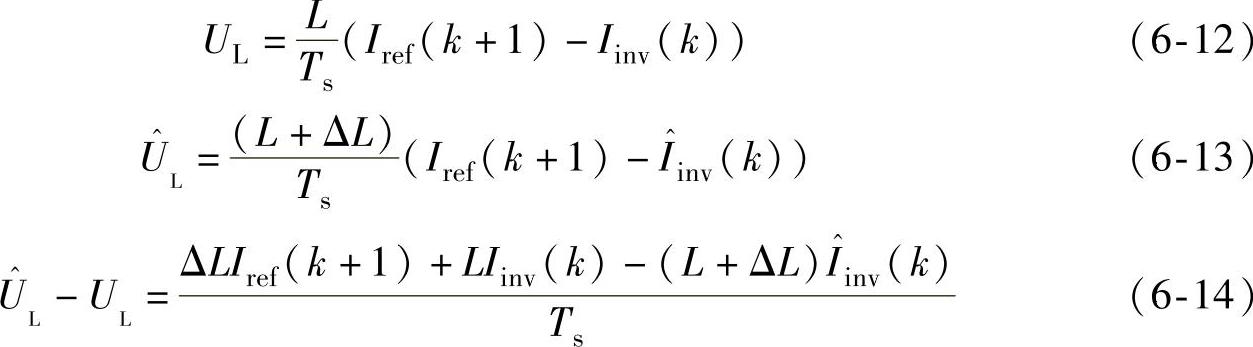
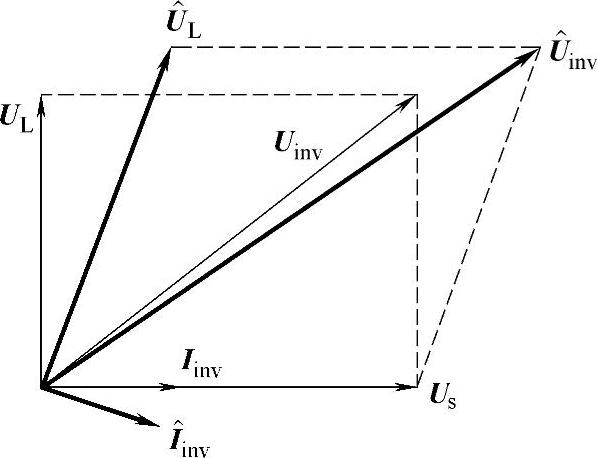
图6-14 电压矢量关系图

当ΔL＞0时，实际电流相对于使用标称电感时要平滑些，由于电流负反馈作用，所以由式（6-13）可知，电感电压幅值会有所增加，电压矢量关系如图6-14所示。其中，I_inv、U_L、U_s和U_inv分别表示实际电感等于标称电感时的逆变输出电流、电感电压、电网电压和逆变输出电压矢量。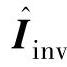、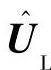和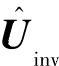分别表示实际电感大于标称电感时的逆变输出电流、电感电压和逆变输出电压矢量。当实际电感增加时，电感电压将由U_L变化到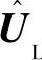,逆变输出电流由I_inv变化到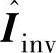，发生了滞后相移，因而参考电流和实际电流之差增大，以满足由式（6-8）计算所得的U_inv达到实际需要的电压水平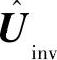。由此可知，当实际电感大于标称电感时，实际电流与参考电流之间存在稳态相位差。而且，当实际电感大到一定程度时，会出现电流幅值大幅下降，而导致系统失去稳定性的情况。

相反，当ΔL＜0时，由于串联电感作用以及单位功率因数控制，实际电流无法发生超前相位，而只能保持与参考电流相同的相位关系。实际电感变小，导致实际电流波动加剧，因此可以保持式（6-8）计算的U_inv在期望的电压附近波动。当实际电感小到一定程度时，导致电流波动达到甚至超出参考电流幅值水平时，电流谐波加剧，系统性能严重下降。

由此可见，预测电流控制是基于精确电路模型的一种控制方式，然而在实际应用时，系统电感参数在运行过程中会发生变化，这时若按照预先确定的控制模型进行控制，就会产生控制偏差，影响控制性能。

3）串联电感在线估计原理：由前面所述可知，预测电流控制是根据逆变输出电压和电网电压之间的关系，使输出电流跟踪参考电流，具有较小电流畸变和谐波含量的优点。该控制方法是在每个开关周期末，采样逆变器输出电流，计算逆变器调制系数，从而达到实时跟踪参考电流的目的，但是当串联电感参数变化超出一定范围时，整个系统可能会变得不稳定。

事实上，若能在线进行串联电感估计，则可以从根本上解决由于电感变化而导致的系统稳定性问题，因此，参考文献［7］提出了一种串联电感参数的在线估计方法。

从式（6-4）可以得出离散的串联电感表达式为

在开关周期（k-1，k）内的串联电感L可用下式进行离散化描述：

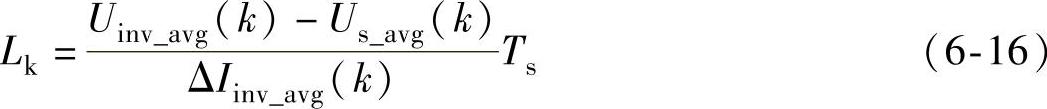
式中，ΔI_{inv_avg}（k）＝（I_inv（k）-I_inv（k-2））/2。

为了避免由于死区影响以及反孤岛检测等因素引起的输出电流过零点畸变对参数估计的影响，因此用于估计滤波电感的采样区间选择应远离电流过零点。考虑到采样区间越短，对采样信号噪声的影响越大，反之，考虑累积误差可能增大的因素，采样区间分别选择在同步旋转角正半周的（π／6，π／2）和负半周的（7π／6，3π／2）范围内。

对式（6-16）取绝对值，且假设在一个采样区间内包含N个整数开关周期，则采样区间内的滤波电感之和如下式所示：

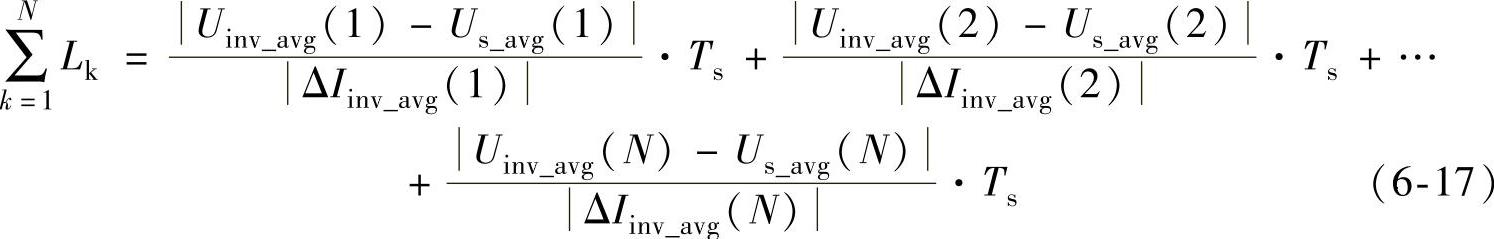
通过下式可以计算得出电流误差的绝对平均值ΔI_avg：

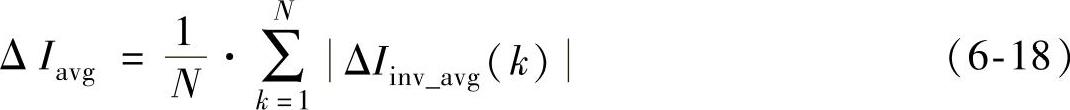
假设一个开关周期的电流变化满足式（6-19）条件，以及逆变器输出平均电压和电网平均电压之差的绝对值如式（6-20）所示，则在一个采样区间内的平均电感可用式（6-21）表示。

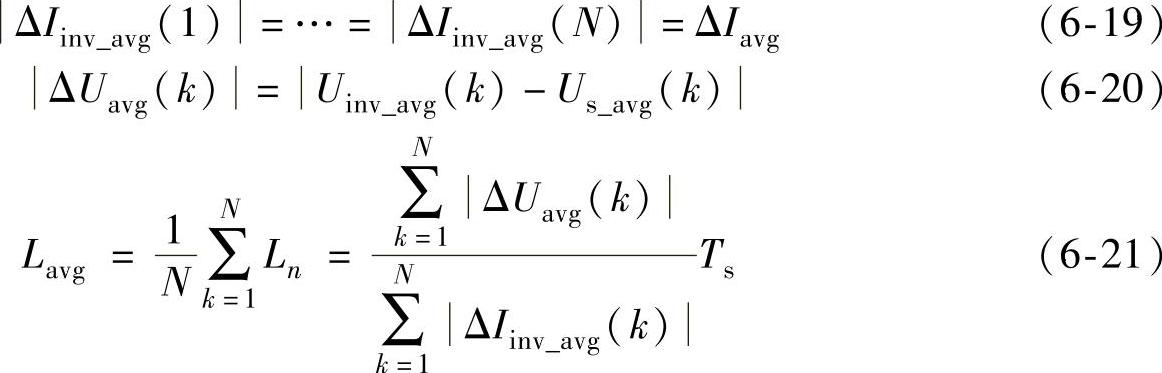
为了避免因尖脉冲噪声干扰以及电网电压突变或负载突变等因素对串联电感估计的影响，采用三点中值滤波法和正负半周两个采样区间进行对比判断的方法进行处理。

假设一个开关周期的电流变化满足式（6-22）条件，则在一个采样区间内的平均电感可用式（6-23）表示。

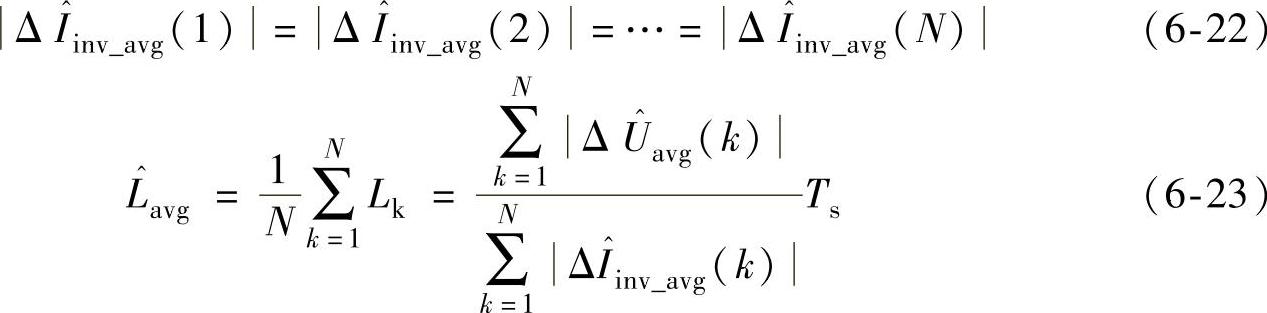
对于一个电网周期内的正负采样区间的电感平均值，若满足式（6-24）条件，则第j个电网周期的电感由正负采样区间电感的平均值表示，如式（6-25）所示。反之，放弃该次估计的电感值。

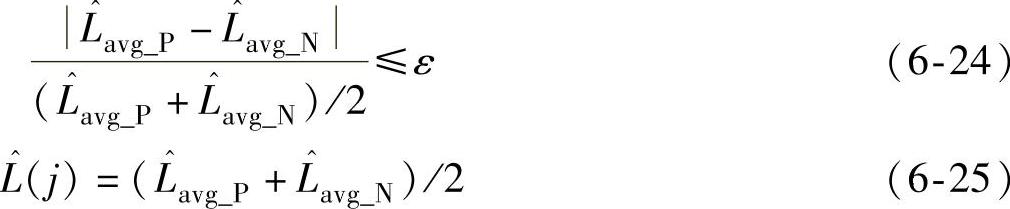
式中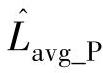、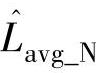——正负半周采样区间估计电感平均值；

ε——常数，一般选择在0.05以内。

利用电感在不饱和情况下必然存在缓慢变化的特点，因此最终的估计电感值采用式（6-26）低通滤波环节再次滤波获得。

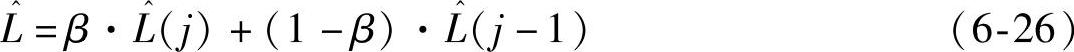
式中 β——常数，且0＜β＜1。

4）仿真结果

利用PSIM仿真软件，进行了仿真研究。仿真参数：标称电感L＝22.5mH，参考电流幅值i_ref＝5A。图6-15和图6-16是实际电感分别变为标称电感值的50％且没有电感估计情况下的仿真结果。图6-15表明实际电感减小50％时，电流波动增加，电流相位与参考电流相位基本一致。图6-16表明实际电感增加100％时，虽然实际电流幅值基本等于参考电流幅值，但是发生了明显的滞后相移。

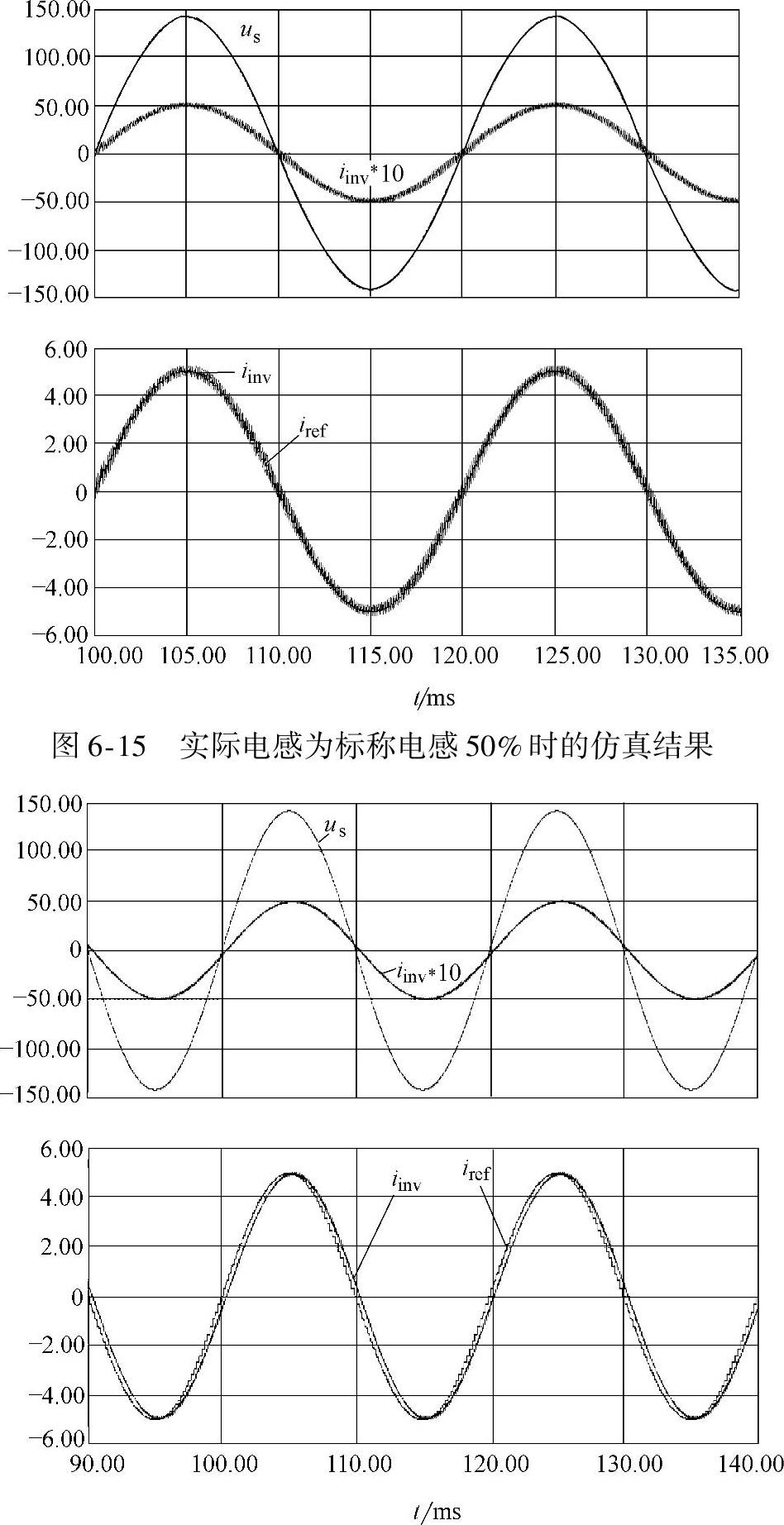
图6-16 实际电感增加100％时的仿真结果

图6-17和图6-18是采用在线电感估计的仿真结果。图6-17是电感L在0.1s和0.2s时刻，分别在45mH和22.5mH之间变化。从图6-17可以看出，尽管电感在很大的范围内变化，但电感估计值都非常准确，而且估计电感的延时时间在交流电网的1个周期以内。图6-18是在0.12s时刻，U_s幅值发生变化且含有15％的3次谐波。它表明电网电压幅值变化以及谐波电压对电感估计的影响很小。

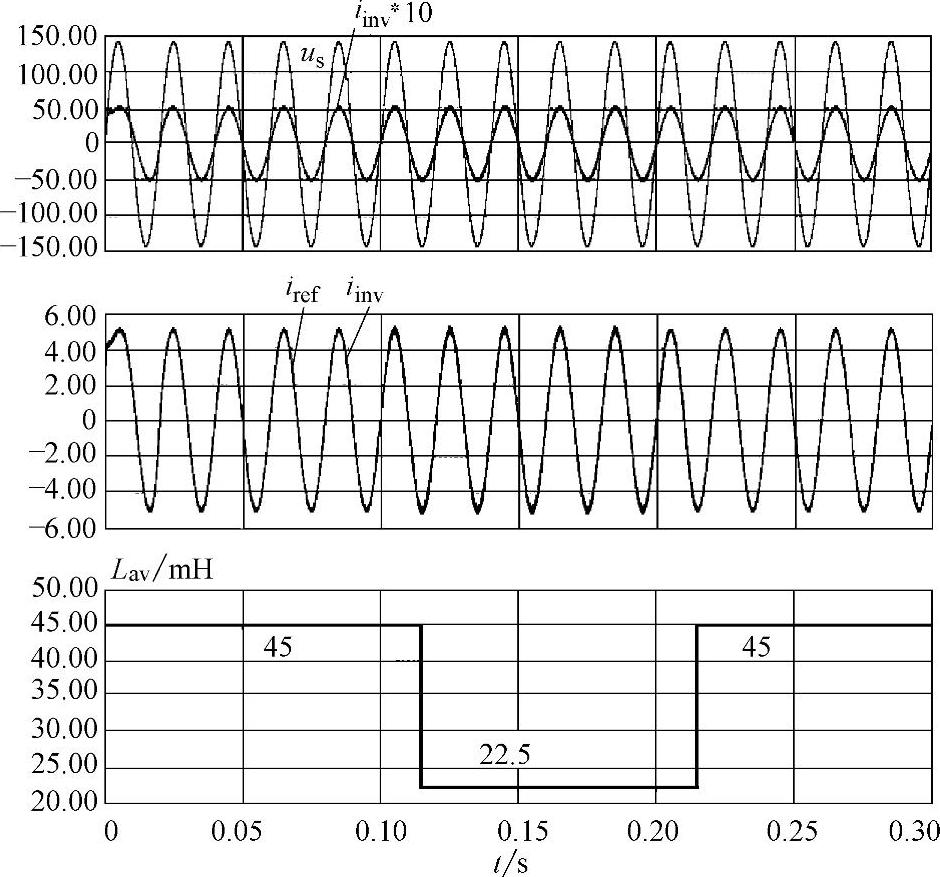
图6-17 电感L变化时的仿真结果

图6-18 电网电压U_s变化且含15％3次谐波的仿真结果

6.2.3.2 单级变换结构

在单级变换结构中，光伏阵列直接通过逆变器并网，省去了中间的DC-DC环节，降低了成本，提高了效率，简化了系统的结构，但最大功率跟踪、电网电压锁相同步和并网逆变控制功能都在一级实现，控制相对于双级结构来说更为复杂。如果该结构不需要变压器升压，则光伏阵列输出电压应满足能够逆变并网的幅值要求。

图6-19为单级结构的光伏发电系统原理框图。并网控制包括MPPT功率外环、直流母线电压中环以及电流解耦控制内环。控制中首先采集光伏阵列输出的电流和电压，经过MPPT运算获得参考直流电压U_dc.ref。根据实际直流电压U_dc与参考直流电压U_dc.ref之差，经过直流电压调节器得到并网有功电流的参考幅值i_d.ref。这里的直流电压调节器除了具有稳定光伏电池板输出电压值的作用外，还具有实现光伏电池板输出功率和并网有功功率的能量平衡作用。单级结构的电流内环控制方法和双级结构的相同，可以采用三相自然坐标系下的直接电流控制，或两相静止坐标系下比例谐振控制，或同步旋转坐标系下的电流解耦控制，这里不再赘述。

图6-19 光伏发电并网的单级主电路结构及控制电路框图