单次谐波电流检测在单相系统中的应用

由上面分析可知，基于瞬时无功功率理论的谐波电流分量检测法是建立在三相电流的α-β变换之上的，三相电流经过变换之后生成了一对正交矢量。因此，如果能够由单相电流生成一对包含电流谐波信息的正交矢量，即可采用相同的结构和策略。

（1）虚拟三相信号法

利用一个周波的单相电流采样数据前后推移120°，可以虚拟一组对称的三相电流信号，再利用图5-6所示原理就可提取单相单次谐波分量信号。设采样的单相电流为A相，每周波采样N点，一个周波的采样数据循环保存在数组i_a［0］～i_a［N-1］中。若当前采样时刻为k，则当前时刻的A相数据为i_a［k］，而由i_a虚拟的当前B相和C相数据分别为

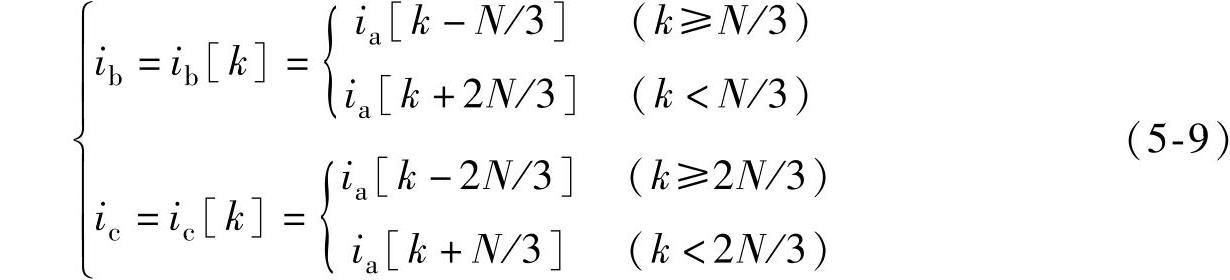
（2）Hilbert变换法

另一种方法是利用理想的Hilbert变换，对单相电流信号进行90°移相，从而构成一组正交矢量。离散Hilbert变换的频域传递函数为

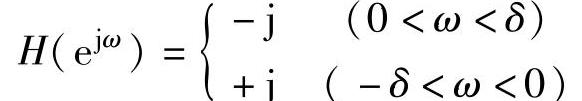
由于直接获得可实现的、稳定的Hilbert单输入单输出滤波系统较为困难，实际应用的数字Hilbert变换系统一般由两组离散实系数的滤波器HF₁和HF₂构成，如图5-7所示。

如果HF₁和HF₂的频率响应分别为HF₁（e^jω）和HF₂（e ^jω），则在所关心频带（ω₀，δ-ω₀）内，HF₁和HF₂的幅频特性应该是全通的，即

HF₁（e^jω）＝HF₂（e^jω）＝1 （5-10）

为了实现Hilbert的90°移相特性，HF₁和HF₂的频率响应还应该满足如下关系：

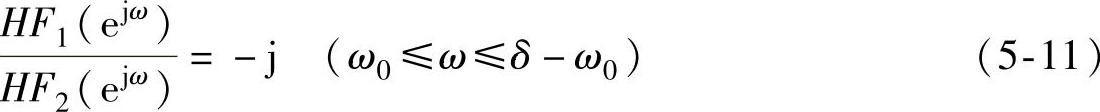
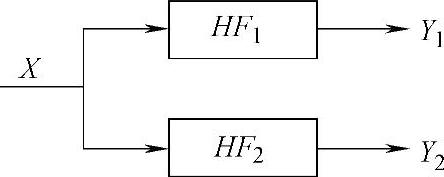
图5-7 Hilbert数字滤波器组

Hilbert滤波器组中的HF₁和HF₂两个模块既可以设计成有限冲击响应（FIR）型数字滤波器，也可以设计成无限冲击响应（IIR）型数字滤波器。Rashid Ansari提出的基于半带滤波器设计IIR型Hilbert滤波器的算法^［8］，在所关心的频带内以及满足幅值精度和相移精度的要求下，相对于其他一些设计方法比较简单，并具有阶次较低，计算量和数据存储量较小的优点。

对于50Hz工频基波信号，若考虑最高谐波次数为18，则本系统可将Hilbert滤波器关心的频率范围设计为40Hz～960Hz，在采样频率为2kHz、相移误差不大于0.0006rad的条件下，Hilbert滤波器组HF₁和HF₂的z函数为［7］

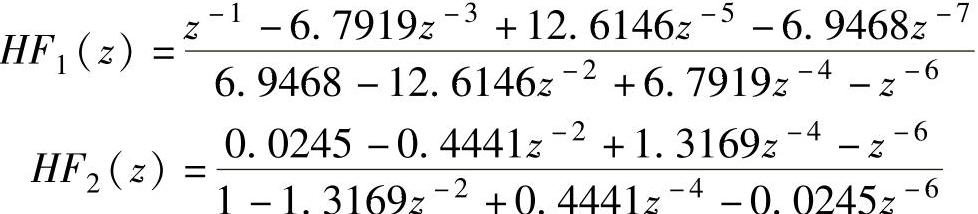
用MATLAB对Hilbert滤波器进行数字仿真，其幅相特性如图5-8所示。

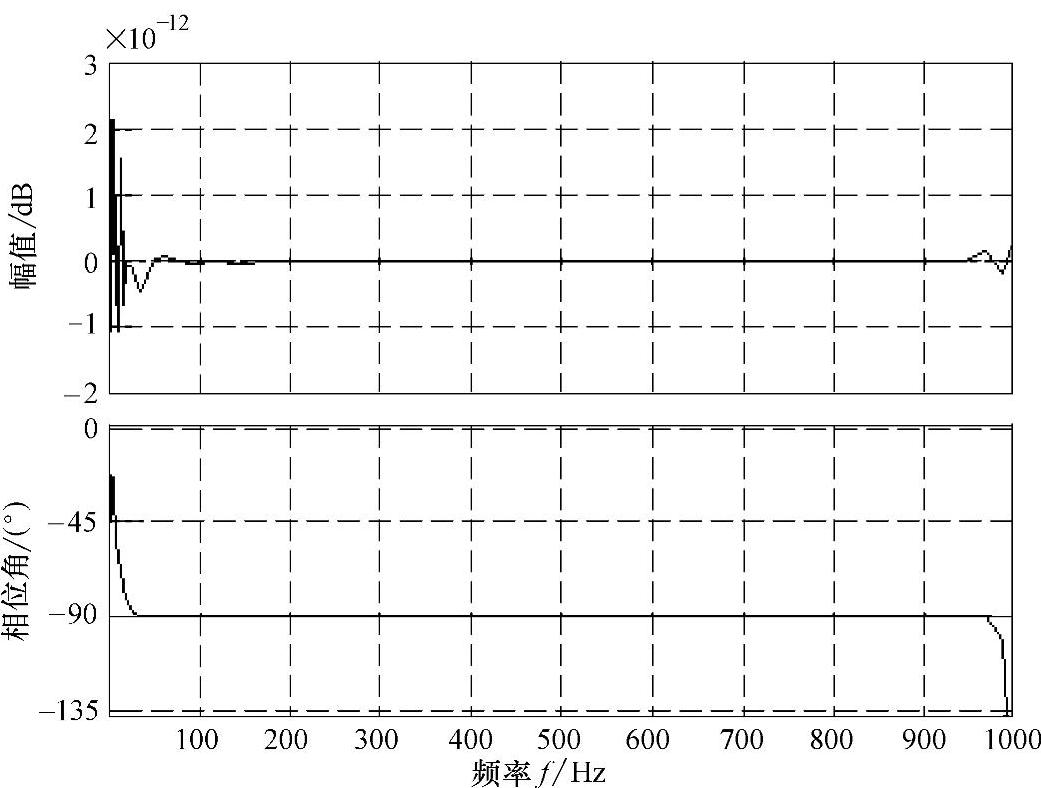
图5-8 Hilbert移相滤波器的幅频和相频特性

（3）傅里叶变换法

采用离散傅里叶变换亦可实现单相单次谐波分量的检测。下面介绍一种基于窗口平移傅里叶变换的单次谐波瞬时波形的检测方法^［9］。

假设原始信号f（t）中含有基波分量f₁（t）和一系列谐波分量f_n（t），其中h次谐波分量是要检测出来的目标谐波分量。以基波分量为相位参考基准，则原始信号f（t）可表达为

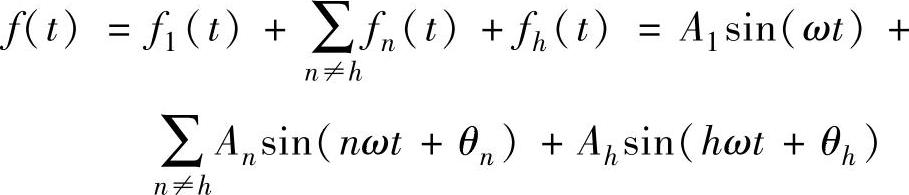(www.xing528.com)

将上式分解后可得

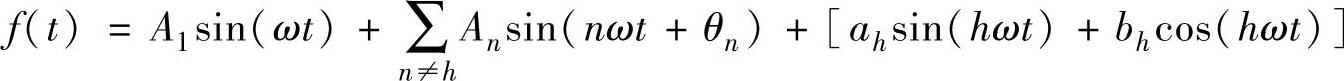
稳态情况下，h次谐波幅值在正弦和余弦正交坐标系上的分量a_h和b_h是恒定不变的常数，但在暂态情况下均为时间的变量，记作a_h（t）与b_h（t）。采用窗口平移傅里叶变换，在时刻t时的h次谐波幅值在正弦和余弦正交坐标系上的分量可以表示为

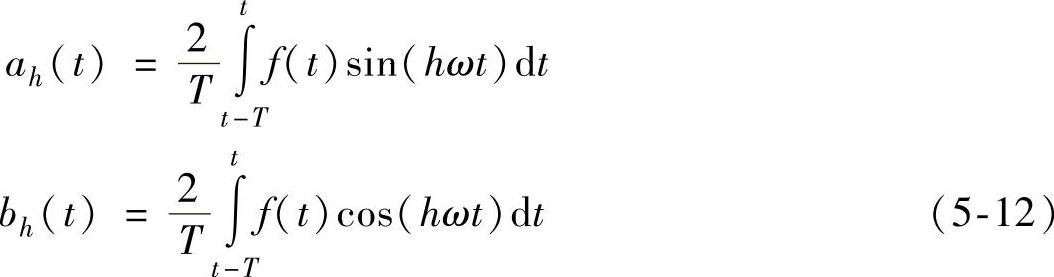
于是，h次谐波分量可以进一步按照下式求出：

f_h（t）＝a_h（t）sin（hωt）＋b_h（t）cos（hωt） （5-13）

根据式（5-12）和式（5-13），可以得到检测h次谐波电流的信号处理流程，如图5-9所示：

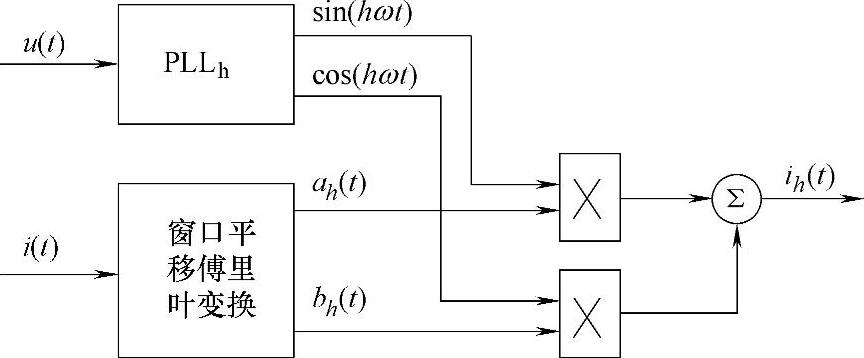
图5-9 基于傅里叶变换的单相单次谐波的检测

在数字信号处理中，采用增量式算法可以简化运算、提高处理速度。对式（5-12）作离散化处理，可得

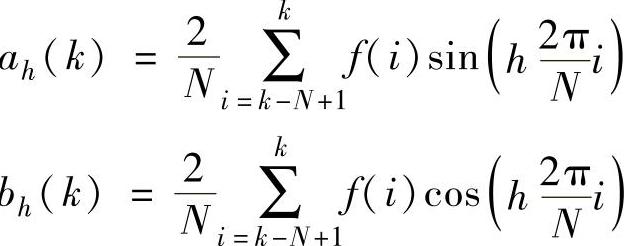
令

Δa_h（k）＝a_h（k）-a_h（k-1）

Δb_h（k）＝b_h（k）-b_h（k-1）

则可得一组适用于微控制器的递推增量式检测算法：

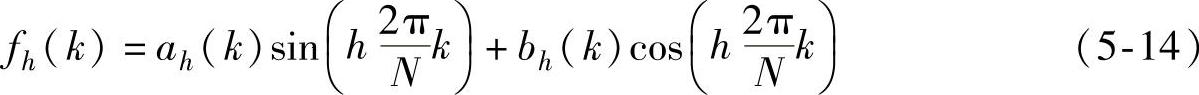
其中

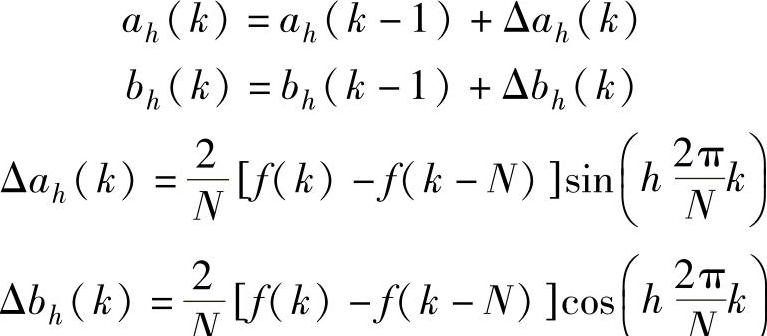
式中 N——离散傅里叶变换的数据长度，即一个基波周期中原始信号的采样点数。

图5-10给出了用DSP实现的单相单次谐波的检测结果，下面波形为基波与13次谐波合成的原始波形，上面波形为检测得到的13次谐波分量。在实际系统的应用中，需要考虑所检测的最高次谐波次数与采样点数的关系，谐波次数越高采样点数则应越多，但DSP本身的性能会约束采样点数的选取。采用TMS320F2812芯片时，一个基波周期内采样1024个点及以上，可以取得较好的检测效果。

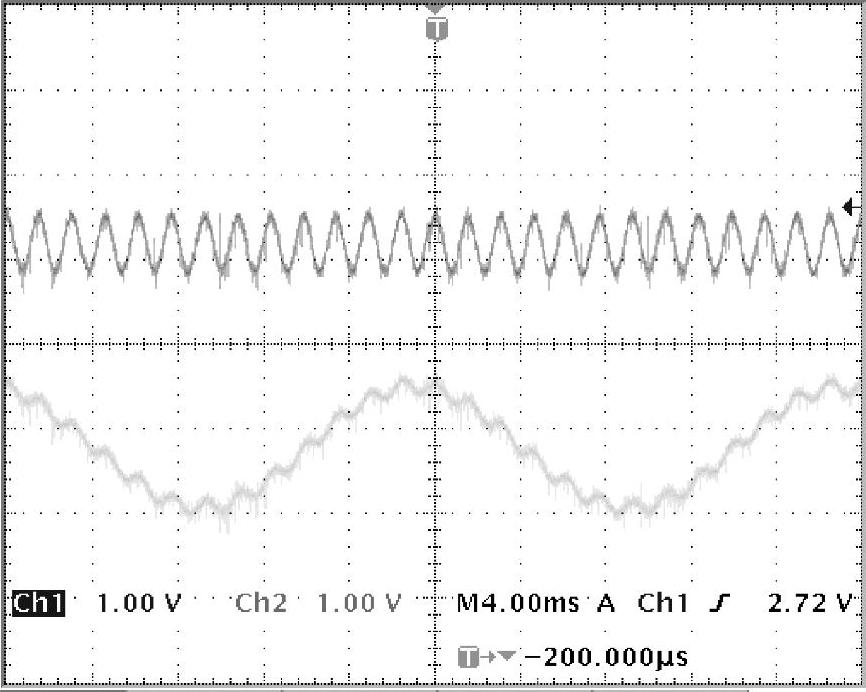
图5-10 基于傅里叶变换的单相单次谐波检测方法的DSP实现结果