VSC-HVDC的矢量控制技术

矢量控制就是将VSC输出的三相交流电压和电流分别用正交同步旋转坐标系中的两个正交分量来表示和分别控制。通常，旋转坐标系与三相电网电压同步旋转，且旋转坐标系的d轴与电网A相电压矢量重合，此时，电流的d轴分量即为有功电流分量，而电流的q轴分量则为无功电流分量。

矢量控制的目标是VSC输出电压的d轴分量和q轴分量，但是为了具有限流功能，矢量控制系统采用了电流内环控制和目标外环控制的双闭环结构。尽管HVDC的有功控制目标仅与电流的d轴分量相关、而HVDC的无功控制目标仅与电流的q轴分量相关，但是电流的d轴分量和q轴分量都与电压的d-q分量相关，存在严重的耦合关系。因此，常在电流内环控制中引入解耦算法。

在d-q同步旋转坐标系下，VSC换流器的数学模型为

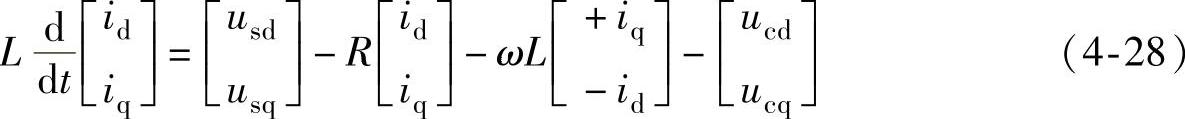
式中，u_sd和u_sq为三相电网电压的d-q轴分量，u_cd和u_cq为VSC三相逆变电压的d-q轴分量。显然，VSC输出电流的d-q轴分量与VSC三相逆变电压的d-q轴分量相互耦合。令

u_d和u_q为一对虚拟的中间变量，则式（4-28）可以改写为

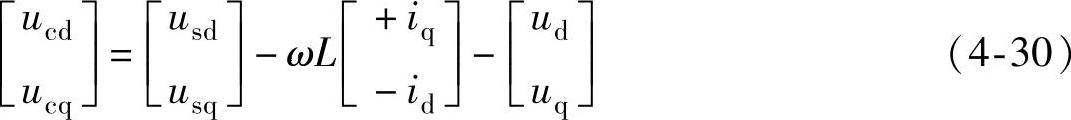
因此，若以u_d和u_q代替u_cd和u_cq作为VSC换流器的新的控制变量，将式（4-30）代入式（4-28），则换流器的数学模型变更为

显然，新模型中VSC输出电流的d-q轴分量仅与VSC三相逆变电压的虚拟同轴分量相关，而与异轴分量无关，即实现了控制上的解耦。解耦后的矢量控制系统结构如图4-23所示。

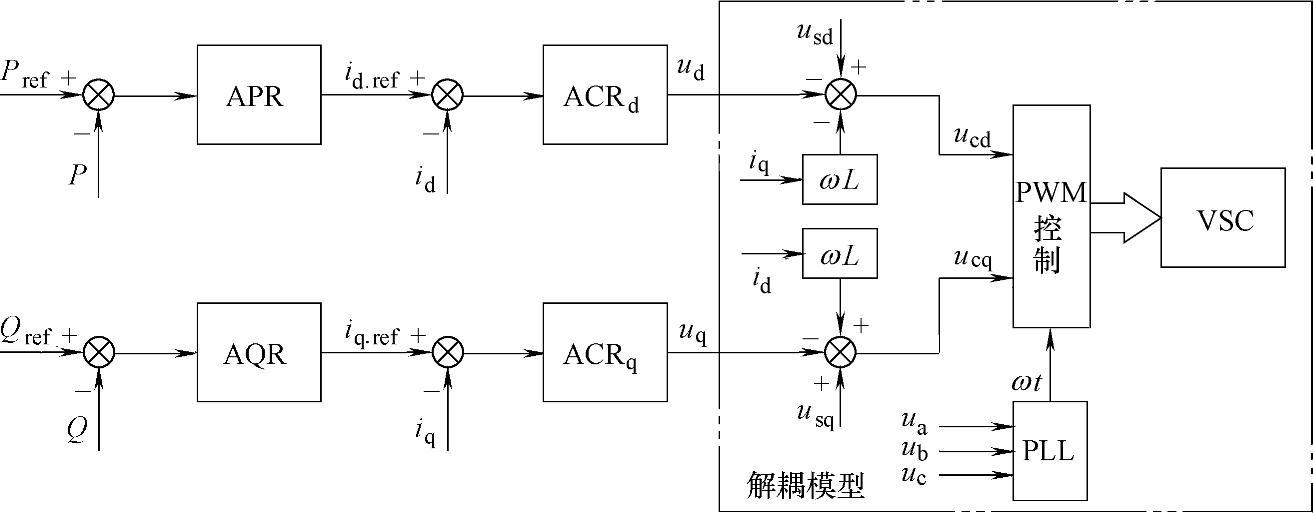
图4-23 VSC-HVDC的矢量解耦控制

电流解耦之后，由式（4-31）可得VSC换流器的传递函数如下：

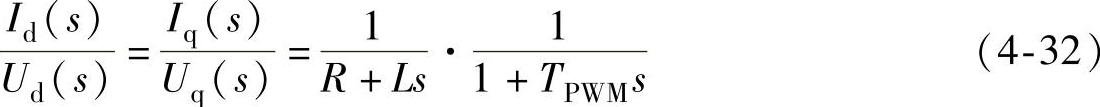
式中第二项惯性环节是考虑到PWM控制的延迟作用而引入的一个近似等效环节。实际中，PWM开关的延迟时间不等，这里可取其统计平均值：T_PWM＝T_s/2，T_s为PWM开关周期。

设U_s为电源线电压有效值，按照习惯取d-q旋转坐标系的d轴与A相重合，此时，u_sd＝U_s，u_sq＝0，且i_d为交流电流的有功分量，i_q为交流电流的无功分量，有功功率和无功功率可表示为

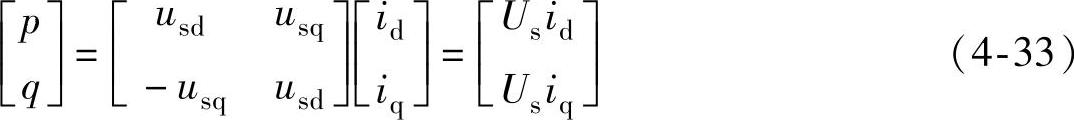
若所有调节器均采用PI控制规律，则VSC-HVDC的控制系统结构如图4-24所示。

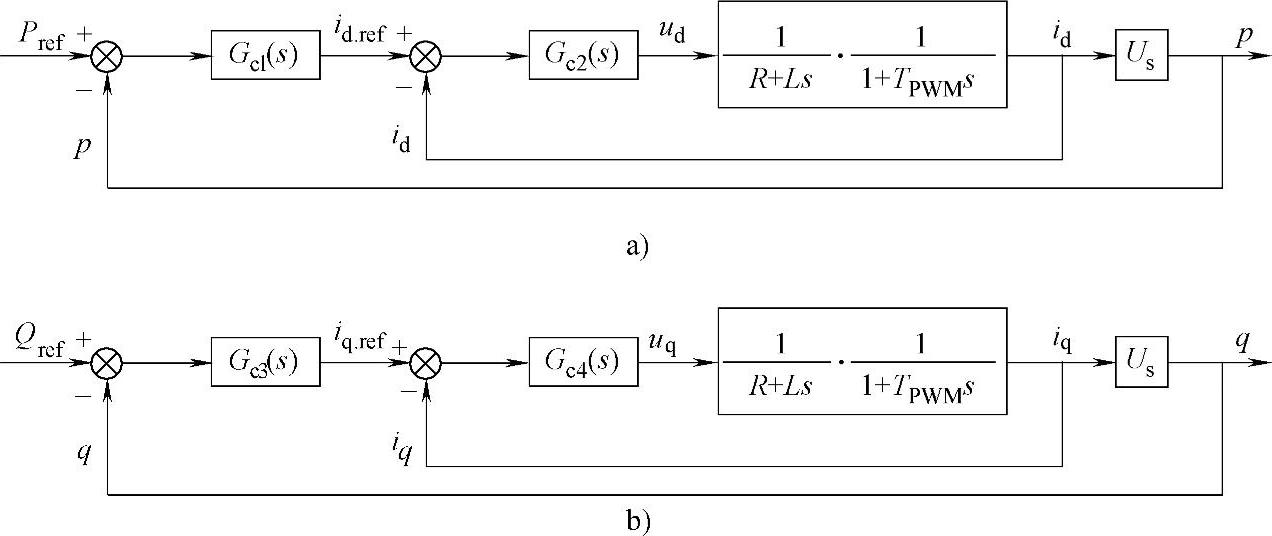
图4-24 VSC-HVDC的矢量解耦控制系统

a）有功功率控制 b）无功功率控制

（1）电流调节器参数设计

若电流内环采取PI控制策略：

则从图4-24可得电流内环的开环传递函数（以有功功率环节为例）：

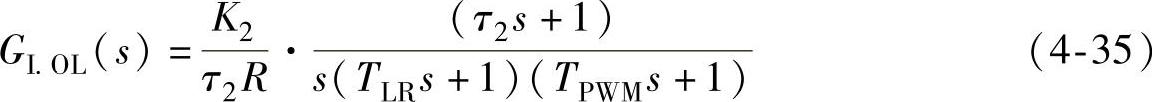
式中，T_LR＝L/R表征VSC交流侧系统的时间常数。选取τ₂＝T_LR，使校正装置引入的零点与原系统中的大惯性极点对消，此时，电流内环系统校正为典型I型系统：

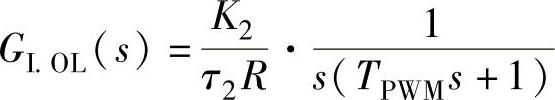
按照典型I型系统的最佳整定方法，取

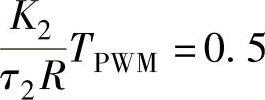
则可得电流内环的PI调节器参数整定值为

按照上述参数整定之后，电流内环的闭环传递函数为

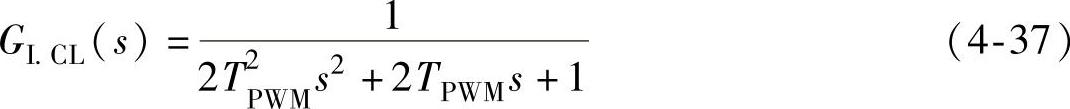
针对表4-5所示的VSC-HVDC仿真示例系统，计算可得电流内环的开环传递函数为

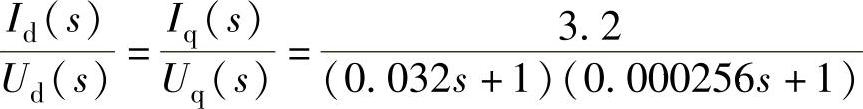(www.xing528.com)

按照上述参数整定原则，PI参数整定结果为：τ₂＝0.032，K₂＝19.5。

一般情况下，T_PWM＜0.001s，忽略式（4-37）中的平方微小项，可得电流内环传递函数的近似表达式：

（2）直流电压调节器参数设计

对于直流电压控制而言，可将另一端换流站等效为一个虚拟电阻R_eq。在额定工况下的虚拟电阻可由额定直流电压U_dcN和额定有功功率P_N按下式计算：

忽略直流传输线上的电阻和电感，则VSC-HVDC系统可以解列为一个常规的PWM整流器或逆变器，如图4-25所示。

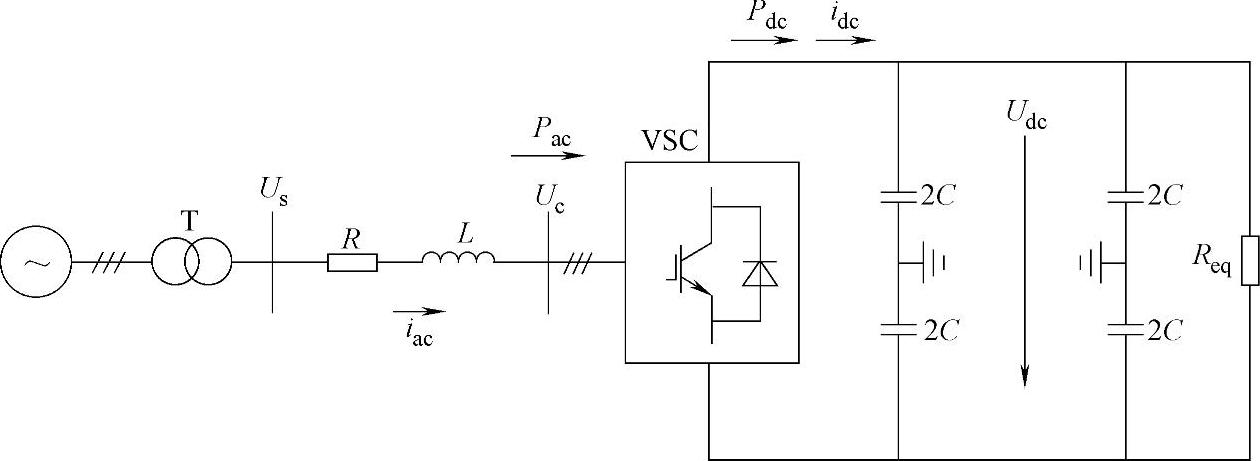
图4-25 定直流电压控制换流器的等效电路

由直流侧电路可得如下电路方程：

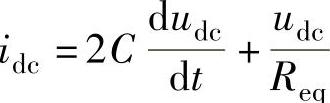
根据换流器交直流侧有功功率平衡，可列写如下方程：

U_si_d＝u_dci_dc

正常情况下，直流电压仅在额定值上下波动，因此上式中的瞬时直流电压可用额定值U_dcN近似替代。此时，由上面两式可以得到直流电压对交流电流d轴分量的传递函数：

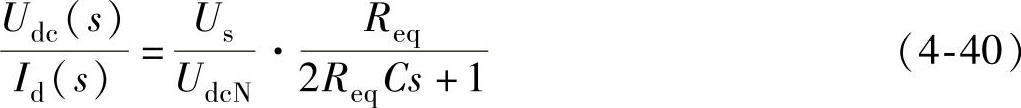
结合式（4-38），可得电流内环校正之后的直流电压外环的系统数学模型如图4-26所示：

图4-26 定直流电压控制环节

若采用PI调节规律，由此可得直流电压外环的开环传递函数为

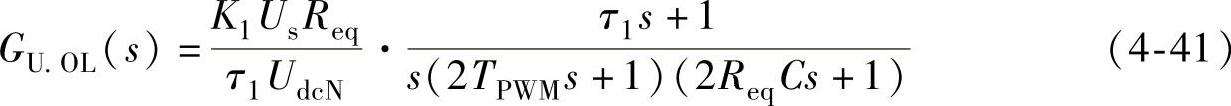
选取τ₁＝2R_eqC，使校正装置的微分零点与原系统中的惯性极点对消，此时，直流电压外环系统校正为典型I型系统：

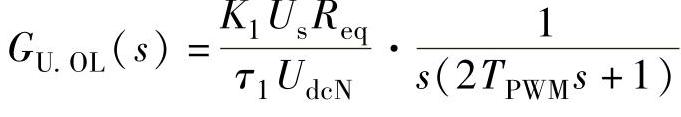
按照典型I型系统的最佳整定方法，取

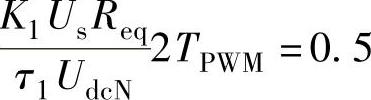
则可得电压外环的PI调节器参数整定值为

针对表4-5所示的VSC-HVDC仿真示例系统，计算可得PI参数为：τ₁＝0.08，K₁＝1.95。若忽略等值电阻的影响，直流电压外环控制系统也可按照典型Ⅱ型系统进行校正，此时的校正结果为τ₁＝0.002，K₁＝1.95。

（3）功率调节器参数设计

设功率调节器仍采用PI控制规律，由图4-24和式（4-38）可得功率外环的开环传递函数为

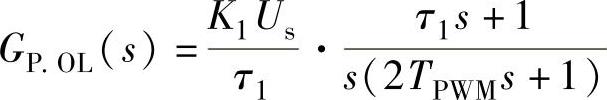
为了抑制PWM开关频率引起的谐波影响，积分时间常数可取τ₁＝10T_PWM，比例系数可按穿越频率来确定。功率外环的频率响应速度应该小于电流内环，同时应使幅频特性曲线以-20dB／sec斜率穿越零分贝线，可取ω_c＝1/（20T_PWM）。于是，功率外环的PI调节器参数整定值为

校正之后，功率外环的闭环传递函数为

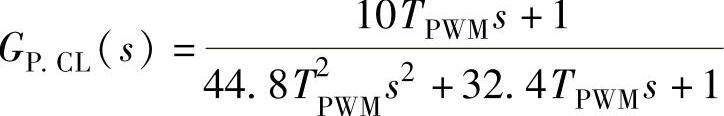
针对表4-5所示的VSC-HVDC仿真系统示例，按照上述参数整定原则，功率外环的PI参数计算结果为：τ₁＝0.00256，K₁＝4.46×10^-5。