VSC-HVDC幅相控制技术优化

幅相控制就是根据控制目标误差，按照反馈控制规律，由调节器直接得到VSC逆变输出电压的幅值和相位，幅相控制也称直接控制。对于基于PWM控制技术的VSC而言，电压幅值可用PWM调制深度λ来表征，而电压相位可用以电网电压实时相位为参考的相角差δ来表征。图4-18为换流器幅相控制系统的原理框图。图中，APR、AQR和AVR分别为有功功率、无功功率和交直流电压调节器，锁相环PLL用于捕获电网电压的实时相位。

在上图中，也可以将控制角δ更换为VSC电压矢量的q轴分量，将调制深度λ更换为VSC电压矢量的d轴分量，但仍属于幅相控制。幅相控制结构简单、响应速度快，主要缺点是没有限流功能，过电流保护困难。

（1）直流电压调节器参数设计

根据式（4-20），可得VSC-HVDC直流电压对控制角的传递函数：

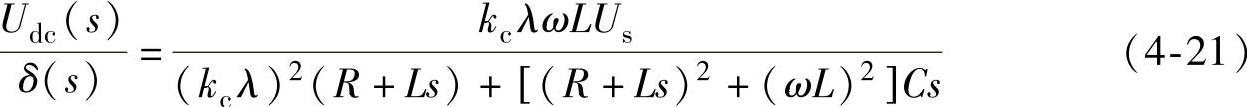
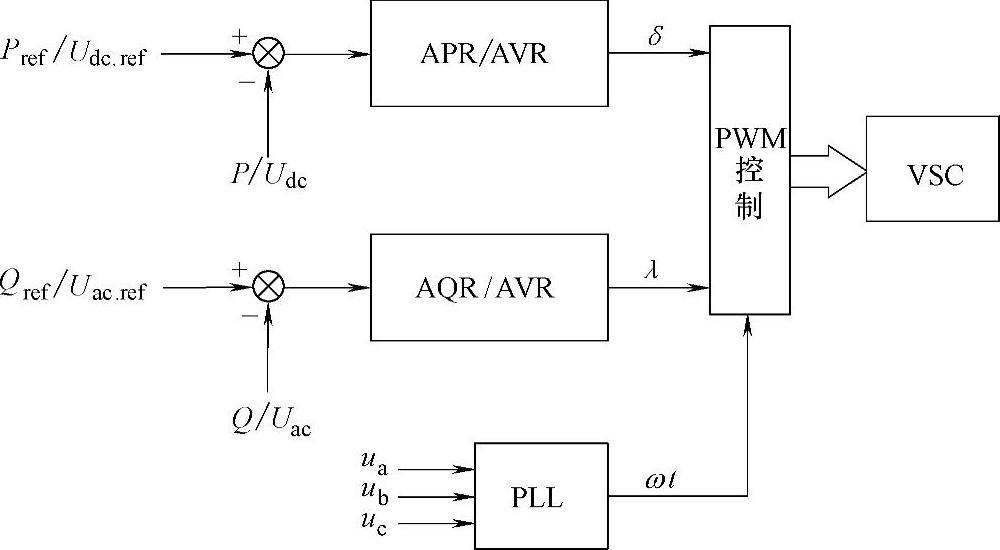
图4-18 VSC-HVDC的幅相控制系统结构

整理可得

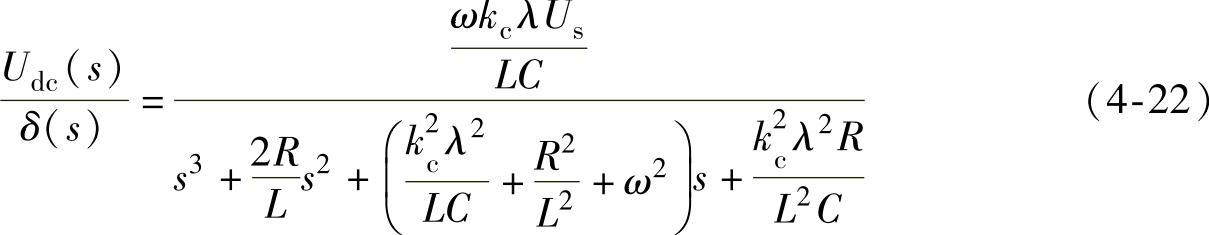
一般情况下，调制深度0.6≤λ≤1.0，因此，上式可按λ_av＝0.8近似处理。

根据系统的传递函数模型，可以按照频率响应法设计调节器的参数。对于上述三阶系统，若采用PI调节规律，根据频率特性与系统稳定性和响应速度的关系，可以参照如下原则计算：

1）选择调节器的积分时间常数等于系统的低频惯性环节的时间常数；

2）系统开环传递函数的幅频特性曲线的穿越频率选择在控制对象的最低两个转折频率之间，使得校正之后的开环幅频特性曲线以-20dB／dec斜率穿越零分贝线。通常，电压源换流器的外环穿越频率可选在10Hz左右^［13］。

针对表4-5所示的VSC-HVDC仿真系统示例，经过计算，可得幅相控制的直流电压系统的开环传递函数为

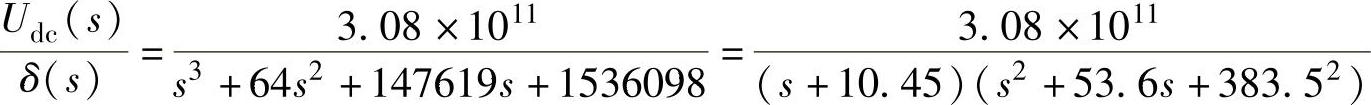
按照上述PI参数选择原则：τ＝1/10.45＝0.096，10.45＜ω_c＜383.5。取ω_c＝2π×10＝62.8rad／s，则计算可得K＝2.92×10^-5。校正之后，直流电压控制系统的开环传递函数如下式所示，图4-19给出相应的波特图，仿真结果详见4.4节。

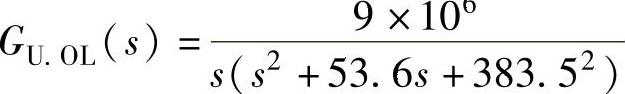
（2）功率调节器参数设计

对于功率控制外环的设计而言，可以认为直流电压由另一端换流器始终维持在

额定值U_dcN。此时，VSC-HVDC系统的两端换流器是解耦的，可以分别独立设计，但功率调节器的响应速度应低于直流电压调节器，以便抑制直流电压波动的影响。根据式（4-20），基于幅相控制的VSC交流侧数学模型近似为(www.xing528.com)

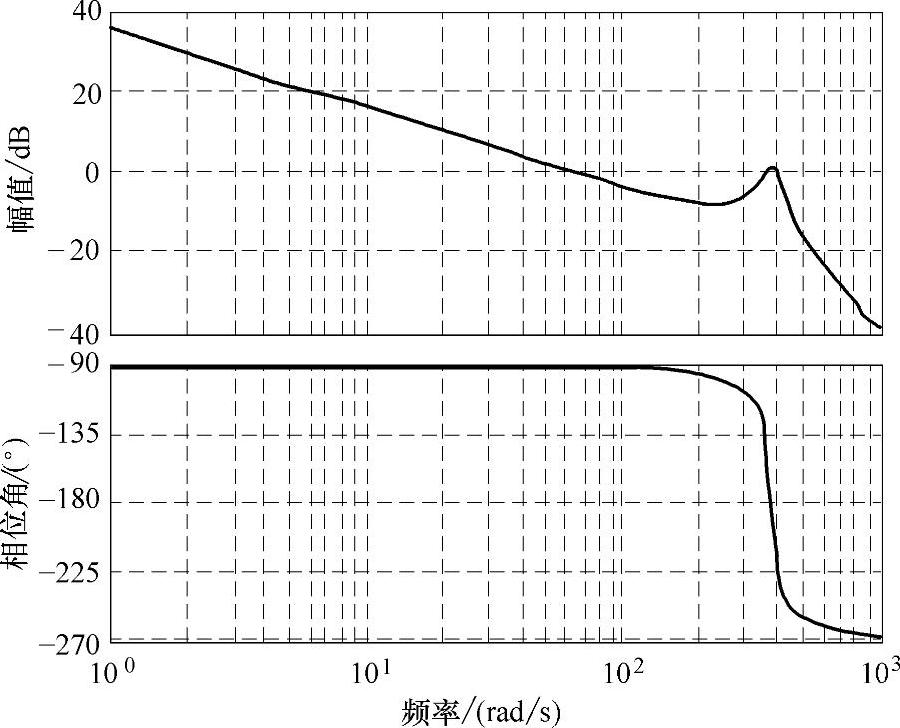
图4-19 校正后VSC-HVDC直流电压控制系统开环波特图

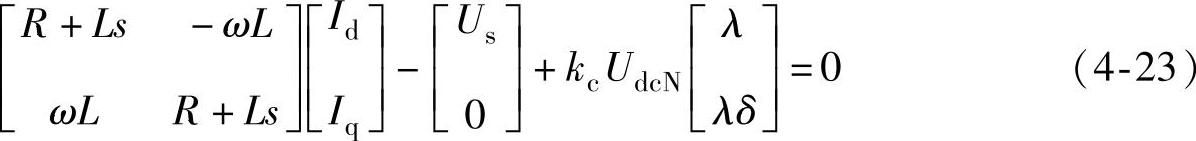
式中，U_s为电源线电压有效值，I_d为交流电流的有功分量，I_q为交流电流的无功分量。求解式（4-23），可得有功电流分量对控制角δ和无功电流分量对调制深度λ的传递函数：

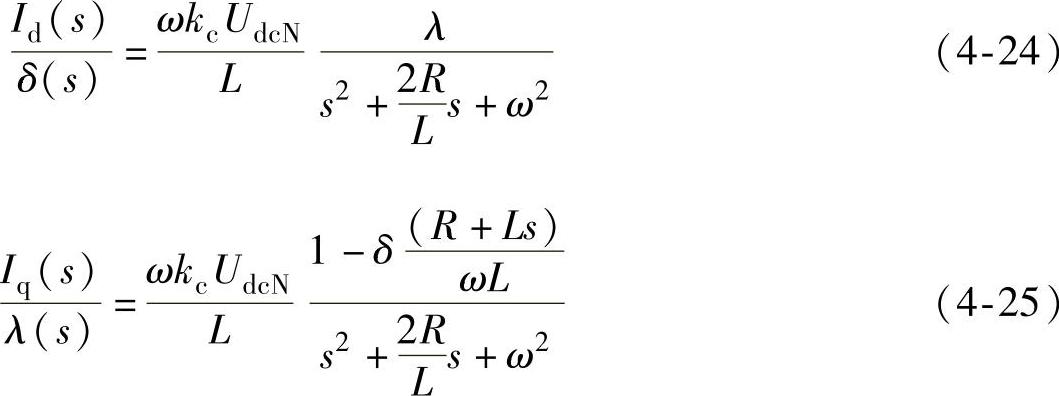
可以看出，有功分量与调制深度λ、无功分量与控制角δ存在一定的耦合。一般情况下，控制角δ≤0.26rad、调制深度0.6≤λ≤1.0，因此，上式可按δ₀＝0、λ_av＝0.8近似处理。显然，上述两式均为二阶振荡环节，转折频率为工频角频率。

设调节器的传递函数为G_c（s），忽略PWM调制引入的微小延迟的影响，则功率幅相控制系统的结构可表示如图4-20所示：

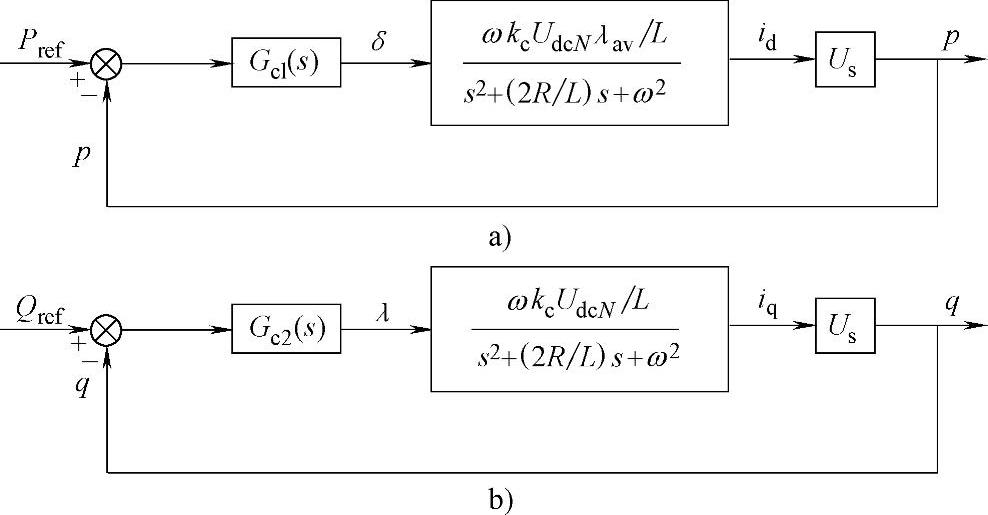
图4-20 VSC-HVDC的幅相控制系统结构图

a）有功功率控制系统 b）无功功率控制系统

若功率调节器采用PI控制规律，此时功率控制的开环传递函数如下式所示：

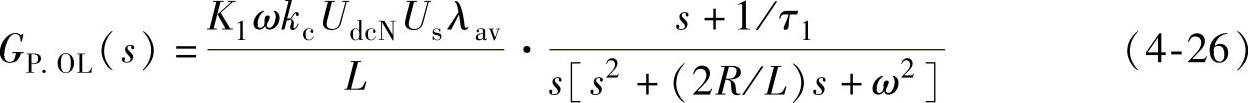
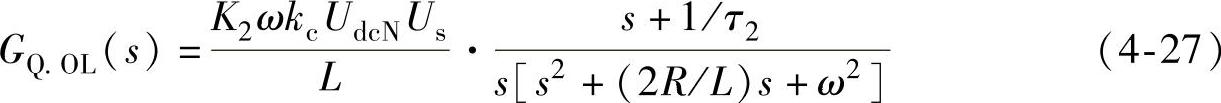
功率调节器的PI参数可按以下原则整定：

1）积分时间常数取为系统转折频率的倒数，即τ₁＝τ₂＝1/ω；

2）比例系数按照穿越频率来确定。在幅相控制中，功率控制系统的响应速度宜低于电压控制系统的响应速度。无功控制系统的穿越频率可取为电压控制系统穿越频率的五分之一，而有功控制系统的穿越频率可取为电压控制系统穿越频率的十分之一，以减缓功率波动对直流电压的影响。

针对表4-5所示的VSC-HVDC仿真系统示例，经过计算，可得幅相控制的功率系统传递函数为

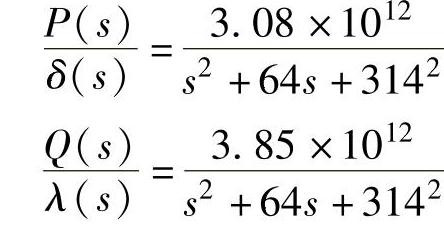
按照上述原则，计算可得τ₁＝τ₂＝1/314＝0.0032，ω_c1＝6.28rad／sec，ω_c2＝12.56rad／s，K₁＝6.4×10^-10，K₂＝1.6×10^-9。仿真结果详见4.4节。