电源电压谐波对直流侧电压和交流侧电流的影响

设电源电压中存在h次谐波电压u_sh，谐波线电压有效值为U_sh，即

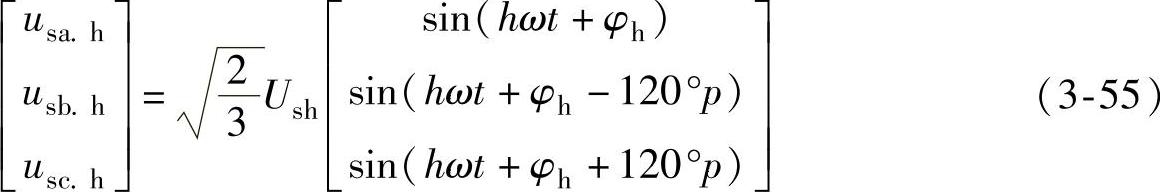
式中，p表示h次谐波电压的相序，正序时p＝＋1，负序时p＝-1。

定性分析已经表明：①电源电压中的谐波分量将引起直流电压的波动，直流电压的波动频率不仅与电压谐波次数有关，也与谐波的相序有关；②某一谐波频率的直流电压波动经过PWM调制将在交流侧产生上下相邻的两个谐波电压分量，进而产生两个谐波电流分量。譬如，5次负序谐波电压和7次正序谐波电压都将引起直流电压的6倍频的波动，反过来，直流电压的6倍频的波动通过PWM控制将在交流侧逆变输出5次负序谐波电压和7次正序谐波电压两个分量。因此，电源电压中的单一5次谐波将会在交流电流中引起5次和7次两个谐波成分。

为了便于定量分析，首先假定由电源电压h次谐波分量引起的直流电压波动分量表示如下：

Δu_dc.h＝d_hsin［（h-p）ωt＋φ₁］ （3-56）

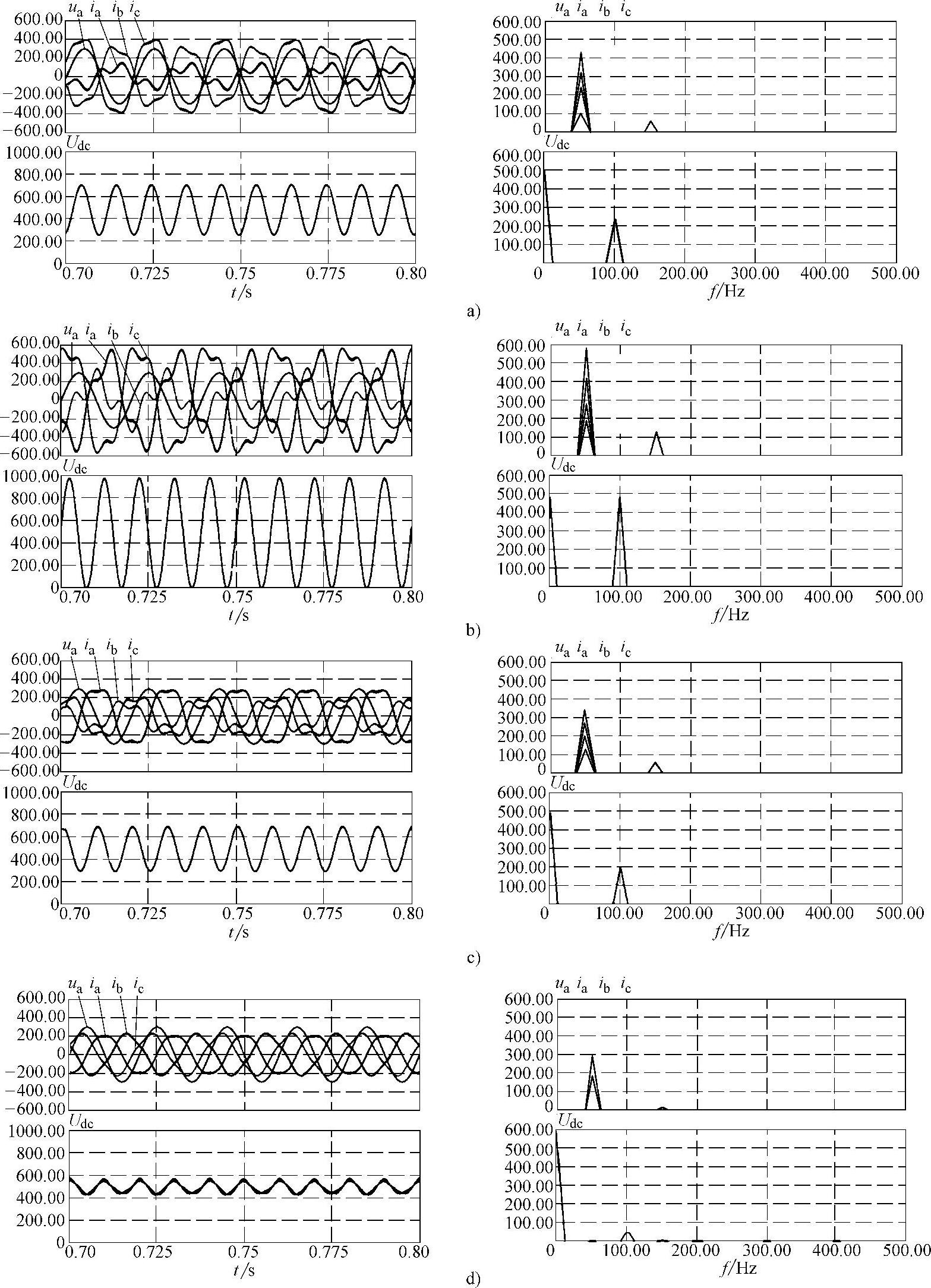
图3-24 电源电压不平衡时SVG交流电流、直流电压波形及其频谱

a）C＝1500μF b）C＝1267μF c）C＝1000μF d）C＝317μF

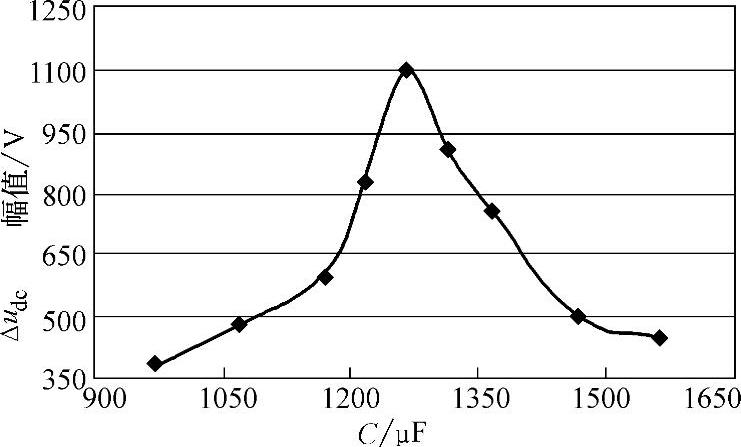
图3-25 直流电压波动随电容的变化关系

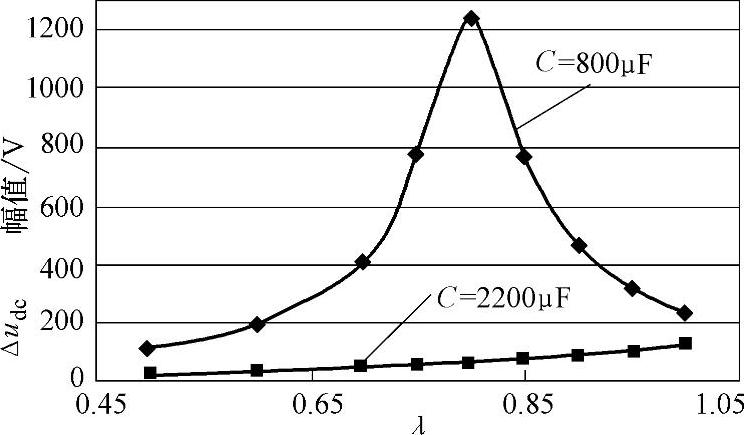
图3-26 直流电压波动随λ的变化关系

则经过PWM调制后，由直流电压波动引起的VSC交流电压的谐波分量u_ch为

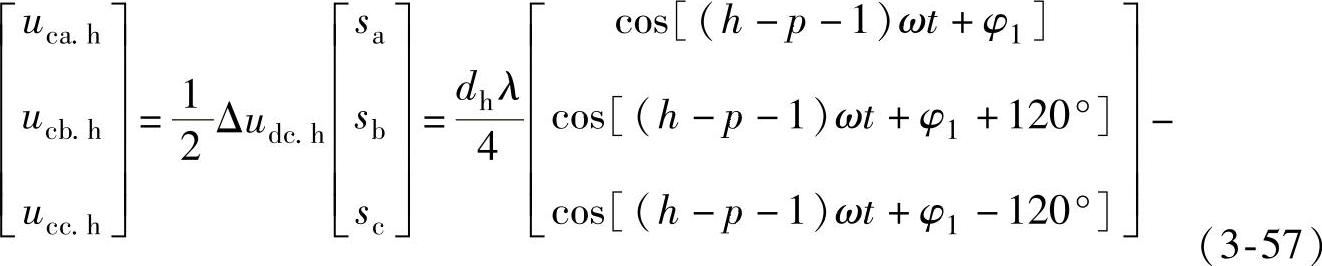(www.xing528.com)

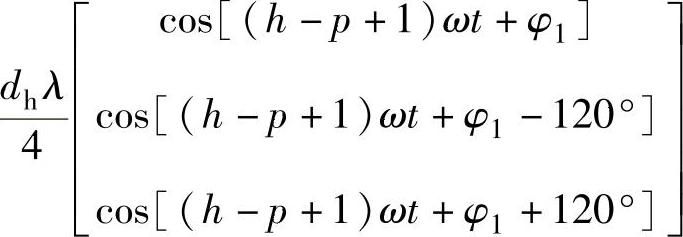
即频率为（h-p）的直流波动电压将产生（h-p-1）次负序谐波电压和（h-p＋1）次正序谐波电压。可以证明，一个谐波电压的次数为h，另一个谐波电压的次数为（h-2p）。于是，若忽略串联等值电阻的影响，由电网谐波电压u_sh引起的交流侧总谐波电流为

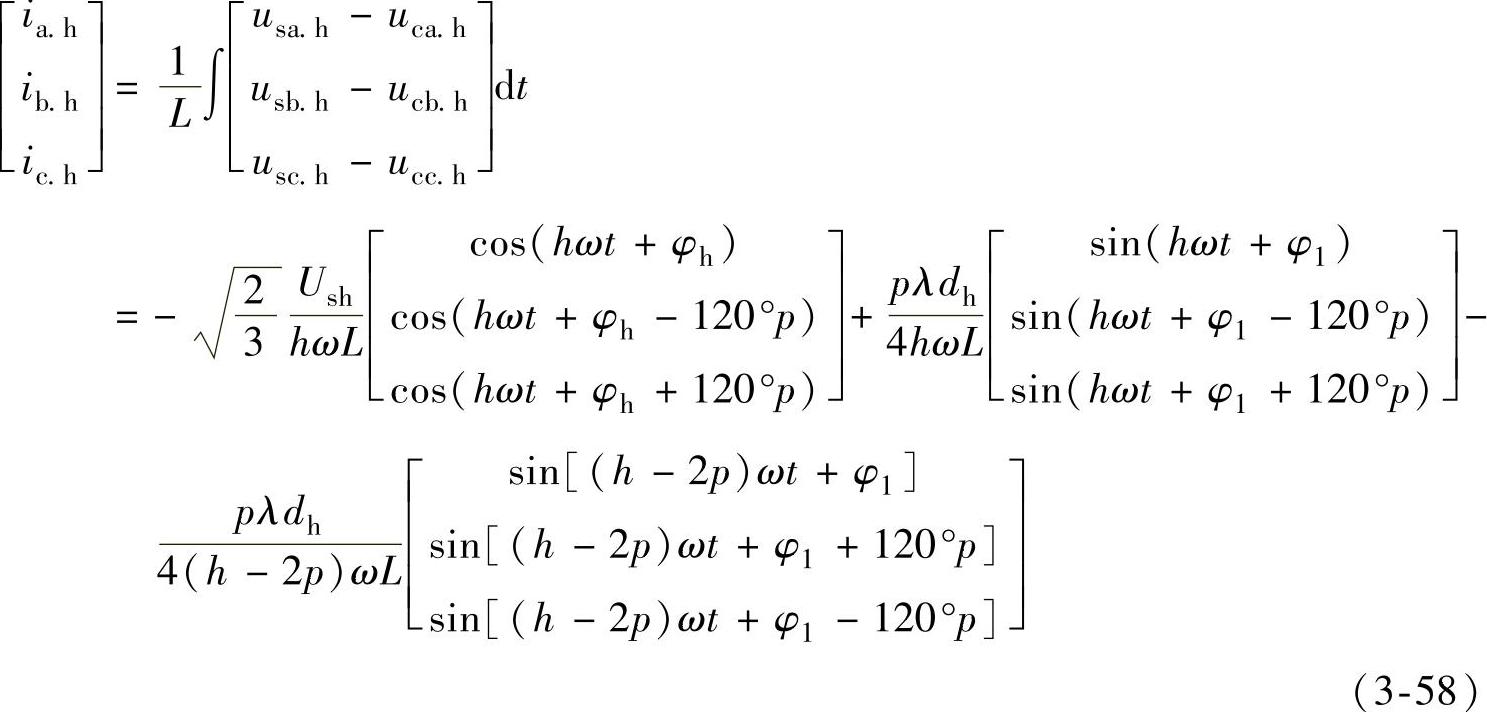
由此谐波电流引起的直流电流波动和直流电压波动分量分别为

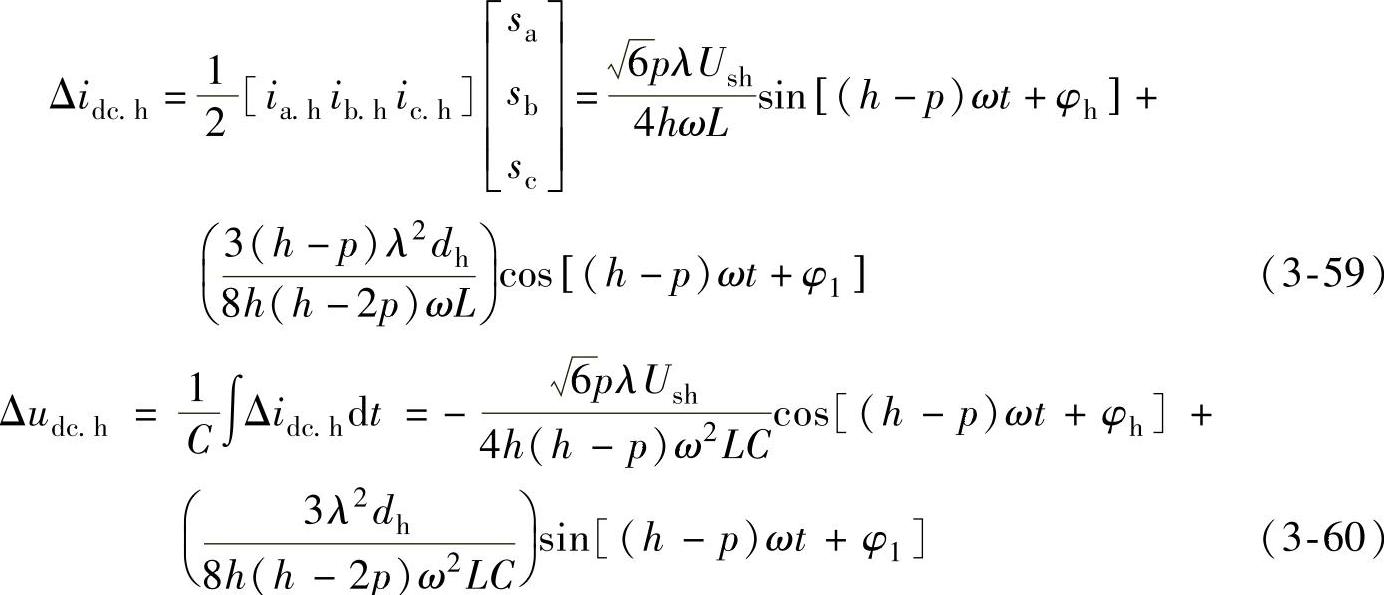
综合式（3-56）和式（3-60），则有

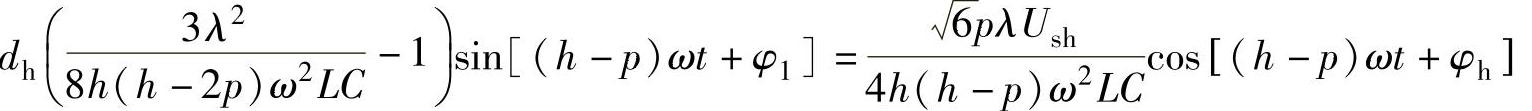
要使上式成立，应有φ₁＝φ_h±90°，于是由h次谐波电压引起的直流电压波动幅值为

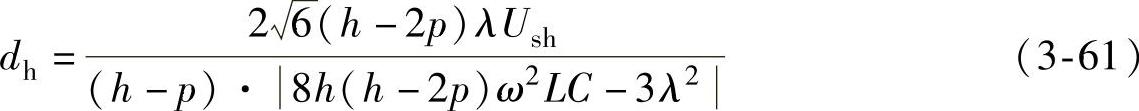
式（3-61）表明，当LC参数和PWM调制深度满足下式关系时

8h（h-2p）ω²LC-3λ²＝0 （3-62）

SVG对由电源h次谐波电压引起的直流电压波动发生了串联谐振。为了避免谐振，LC的取值必须躲过谐振点。

根据式（3-62），在λ＝1的情况下，当L＝1mH、C＝109μF时装置对5次负序谐波电压和7次正序谐波电压发生谐振。图3-27给出了在电源含有5次负序谐波或7次正序谐波情况下电容C取不同数值时直流电压和交流电流的仿真波形，明显可以看出：①直流电压出现严重的6倍基波频率的波动，交流电流同时含有5次和7次谐波分量；②当C＝109μF时直流侧电压波动最大，而当电容减小或增大时直流电压波动均下降。

对于他励控制系统而言，直流电压由外部决定，假设不受直流电流波动的影响而保持为一个常量，此时，VSC仅逆变输出基波正序分量，只有电源电压中的负序分量或谐波分量在串联电抗器中产生相应的负序电流和谐波电流，则不会存在谐振问题。另外，直接电流控制策略也不存在谐振问题。