自励单变量控制系统参数设计技巧

自励单变量控制实际是一种脉冲幅度调制方式，由于调制深度恒定不变，在一个基波周期内，各个脉冲的宽度同比不变，无功功率的调节是通过直流电压随动变化来实现的，这种控制策略可用图3-17表示。

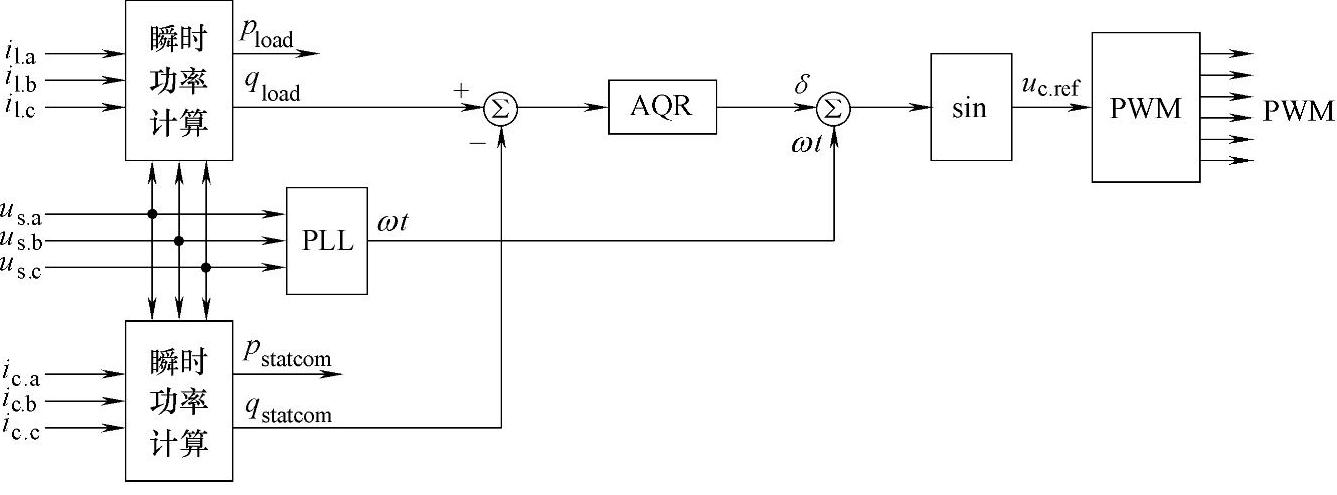
图3-17 基于控制角的自励单变量控制策略

图中，锁相环单元PLL用于提取电源电压的瞬时相位，瞬时功率计算单元分别求取即时负载无功功率和SVG发出的无功功率，根据无功功率误差的大小和方向，通过无功调节器AQR得到期望的控制角。由控制角查正弦函数表可以得到VSC的三相电压调制波形，进而由PWM产生单元生成PWM脉冲信号。PWM可以采用SPWM、SVPWM或优化PWM策略等。

无功功率调节器（AQR）可以采用不同的控制规律。近年来，学者提出了多种可应用于SVG的控制算法，如滑模变结构控制、无源性控制、非线性控制、神经元控制、模糊控制、自抗扰控制等。但是，由于电力系统参数的不可预见性和负载随机变化，要求应用于电力系统控制装置的控制算法具有很强的鲁棒性，因此工程实际中仍然以鲁棒性良好的PI控制规律为主。

根据式（3-32）所示的自励方式下SVG的数学模型，忽略PWM调制引入的微小开关延迟，可得无功电流对控制角的传递函数（略去由于无功方向定义而引入的负号）：

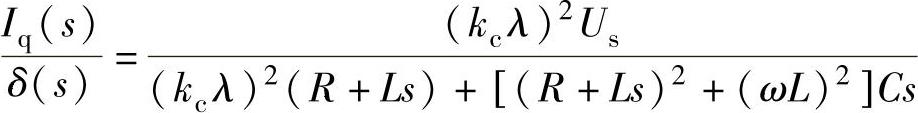
整理可得

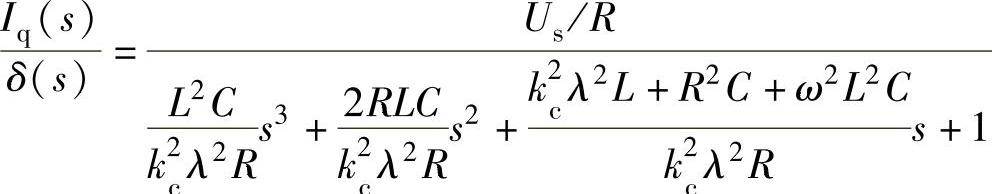
于是，无功功率对控制角的传递函数为

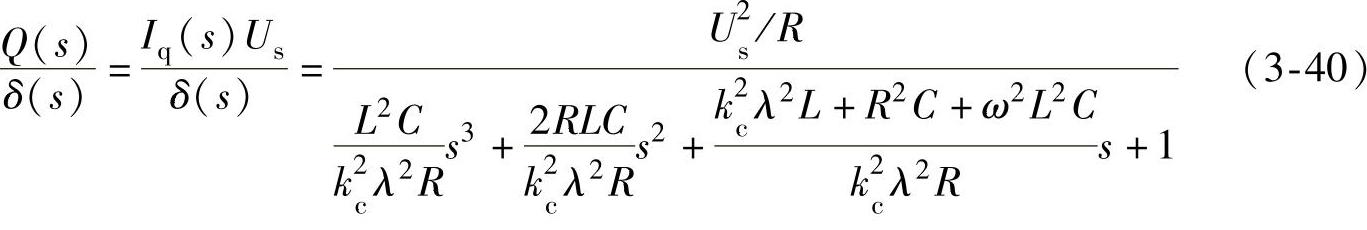
显然，式（3-40）是一个高阶系统。为了简化分析，可以根据SVG的实际情况进行化简和降阶处理。在SVG系统中，通常有如下关系：

L²C＜＜2RLC＜＜ω²L²C

R²C＜＜（ωL）²C因此，无功功率对控制角的传递函数可以简化为一个惯性系统：

式中(www.xing528.com)

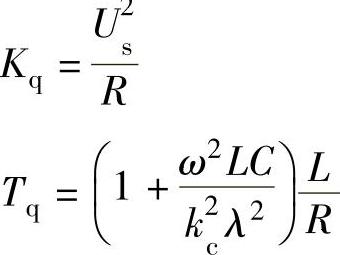
于是，可得图3-18所示的SVG自励单变量

控制系统简化框图。

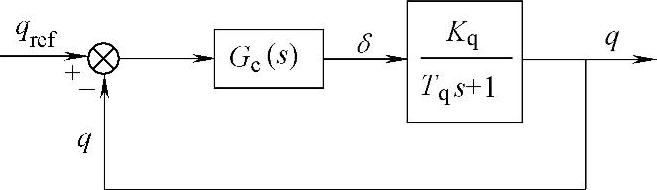
图3-18 SVG自励单变量控制系统简化框图

若调节器采用比例积分环节，则无功功率控制系统的开环传递函数为

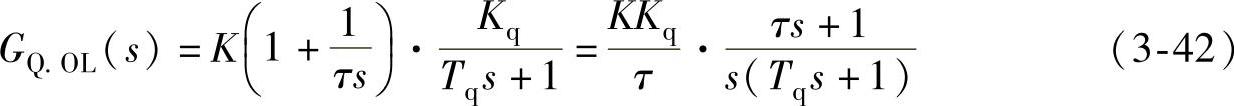
如果取积分时间常数

τ＝T_q/10 （3-43）

则无功功率控制系统可近似为一个典型I型系统。按照典型I型系统的二阶最佳整定方法：

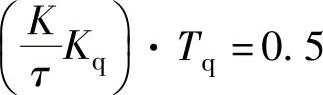
可得比例系数的计算公式：

按照上述校正方法，可以保证无功功率的幅频特性以-20dB／dec的斜率穿越零分贝线，使得系统稳定，但是穿越频率较低（ω_c≈1／2T_q），系统响应速度较慢。因此，也可把PI调节器的零点设置在惯性环节的转折频率处，使系统的微分零点与积分极点相抵消，再按照穿越频率确定PI调节器的比例系数，详见下节仿真示例的具体分析。