三相电力坐标变换和方向定义解析

在三相电力系统中，理想的三相电压和电流是三相对称的正弦波，在abc三相静止平面坐标系上彼此互差120°。若三相电压和电流平衡，则三相电压和电流可以用两相静止直角坐标系（常称αβ坐标系）或两相旋转直角坐标系（常称dq坐标系）下的一对正交分量来表示，从而简化分析。三相电压和电流在三相abc坐标系、αβ坐标系和dq坐标系下的表示可以相互转换，但是转换公式变化灵活，易于引起混淆，本书统一规定如下。

（1）三相电压和电流的表示

三相电压和电流统一用正弦函数来表示，并设abc三相参数依次超前120°。譬如，具有初相角φ的三相电参数x（x代表电压或电流）表示如下：

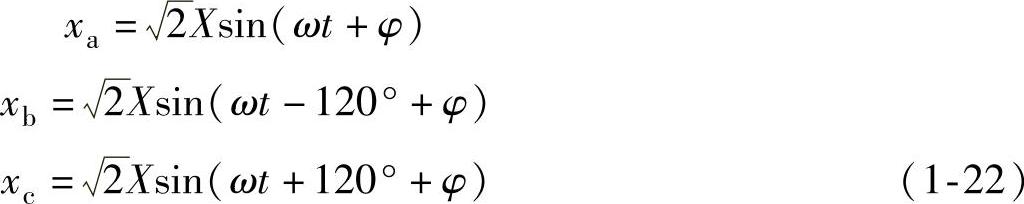
（2）三相abc坐标系与电压电流矢量

三相电压或电流可以用三相abc平面静止坐标系上的一个合成旋转矢量来表示：

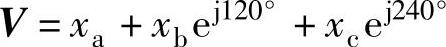
旋转矢量以角速度ω逆时针方向旋转，如图1-8所示。此时，旋转矢量V在abc三个静止坐标轴上的投影即为三相电压或电流。

（3）αβ坐标系及其变换

建立一个αβ静止直角坐标系，设α轴与三相abc静止坐标系的a轴重合，而且αβ轴的排列次序与abc轴的排列次序相同，如图1-9所示。此时，三相电参数（x_a，x_b，x_c）也可以用三相合成矢量V在αβ轴上的投影或分量（x_α，x_β）来表示。

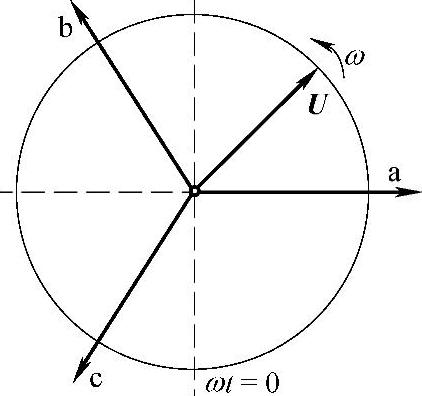
图1-8 三相abc静止坐标系

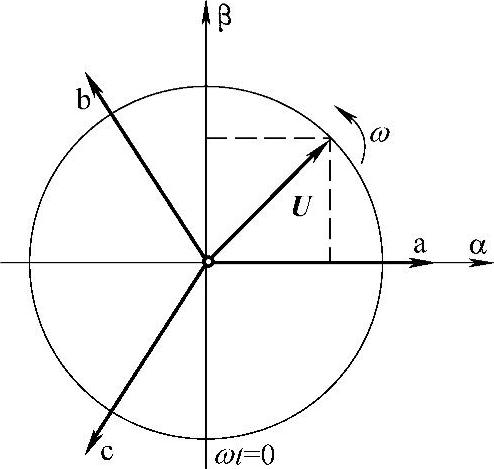
图1-9 αβ静止直角坐标系

由图1-9可知，两种坐标分量的变换关系如下：

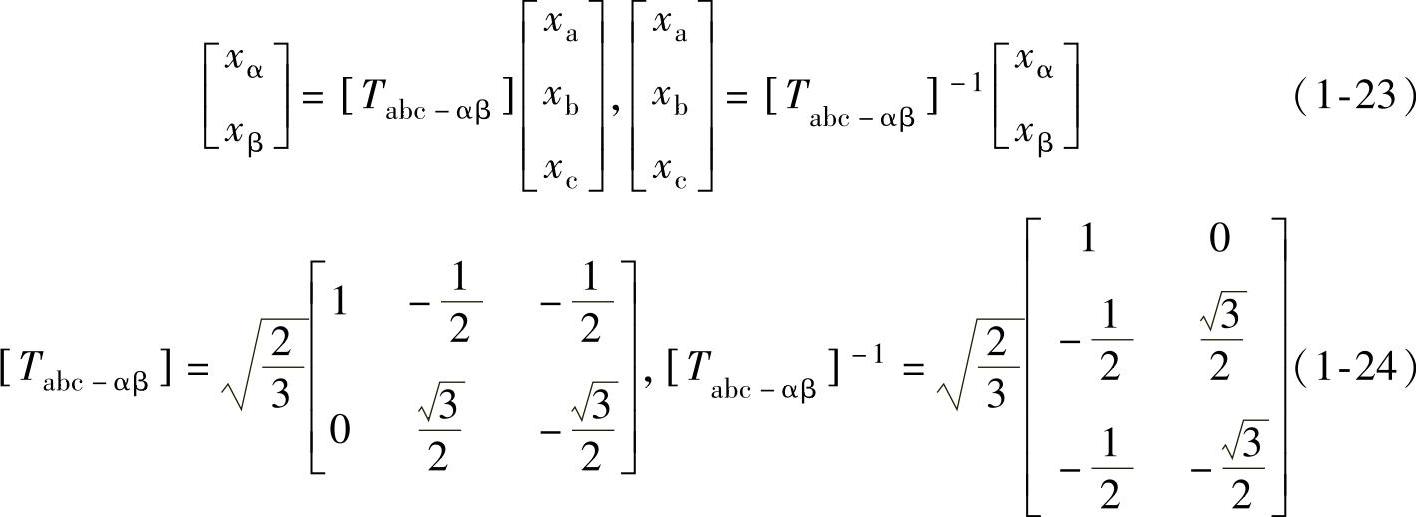
根据αβ坐标分量，瞬时功率可以计算如下：

(www.xing528.com)

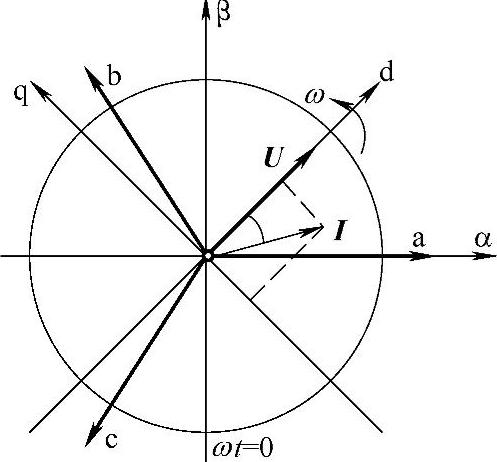
图1-10 dq旋转直角坐标系

值得指出，由式（1-25）计算所得的无功功率以容性无功功率为正。

（4）dq坐标系及其变换

建立一个dq旋转直角坐标系，dq坐标系以与电压电流矢量相同的角速度逆时针旋转，且设d轴与三相参考矢量（常选用电源电压矢量）重合，dq轴的排列次序与abc轴及αβ轴的排列次序相同，如图1-10所示。由于dq坐标系与旋转矢量同步旋转，因此旋转矢量在dq坐标轴上的投影不随时间变化，即dq轴上的电压电流分量为常量。

dq坐标分量与abc坐标分量的变换关系如下：

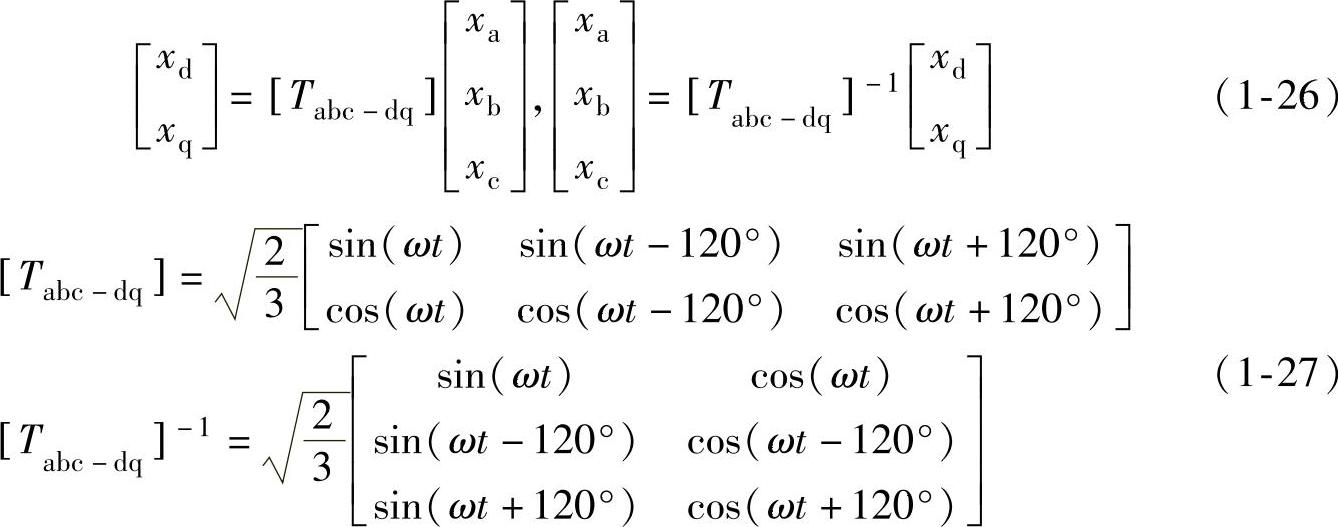
dq坐标分量与αβ坐标分量的变换关系如下：

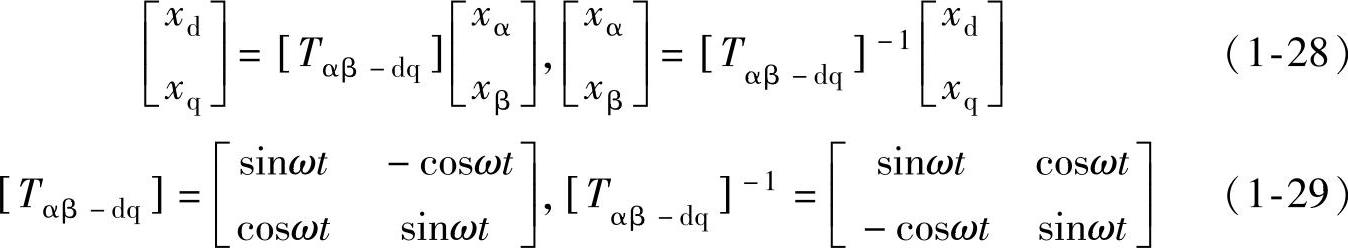
根据dq坐标分量，瞬时功率可以计算如下：

值得指出，由于d轴与电压矢量同轴，因而d轴分量为有功分量，q轴分量为无功分量。按照上述变换关系，q轴分量以容性无功功率为正，瞬时无功功率也以容性无功功率为正。

（5）相位角与功率方向

为了保持电参量的方向在经过坐标变换后的一致性，本书在涉及VSC的分析计算和控制中，对相角和功率的方向统一规定如下：

1）相角以逆时针超前为正；

2）有功功率以VSC工作于整流状态为正；

3）无功功率以VSC发出容性无功功率为正。