碾压遍数计算方法优化

碾压机械碾压时，按照一定次序不断地连接振动轮轴线构成连续相接的四边形，碾压过的区域可用这些四边形描述。碾压遍数是碾压机械碾压过程中通过同一空间位置的次数，也就是碾压过的区域覆盖该空间位置的次数。可用网格法来计算碾压遍数，它是将整个碾压区域划分为一个个阵列式的规则方格，每生成1个四边形则处于该四边形内的方格被碾压了1遍，其遍数累加1，其原理见图6.11。图中碾压区域含两块，采用不同颜色代表不同遍数。

碾压机械碾压中，每一个采样时刻振动轮位置数据都由测量机器人传输至计算机存储并计算。假设至计算碾压遍数时一共记录了N个采样时刻（t1，t2，…，tN）的数据，网格法计算碾压遍数的步骤如下：

（1）将整个碾压区域网格化，并将每个方格的遍数初始化为0，定义整数型变量count，i，j，令count=0，i=1，j=2。

（2）寻找满足如下条件的tj：①j＞i；②棱镜在ti和tj时间内移动的距离dij＞d0，d0为一给定距离常数；③ti和tj在时间上最接近。若找到tj，则令count=j，若找不到tj，则令count=j=N。将ti和tj时刻的碾压机械振动轮位置生成一个四边形S，然后，令i=j。

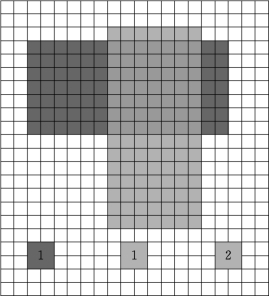
图6.11　网格法计算碾压遍数

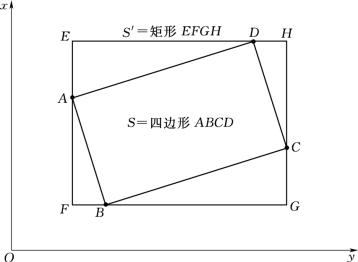
图6.12　方格的搜索区域S′(www.xing528.com)

（3）根据S确定方格的搜索区域S′（S′的确定方法见图6.12）。

（4）按照一定空间次序，遍历S′内每一个方格，判断其是否在S内，若判断成立则该方格遍数累加1。

（5）若count≥N，则计算碾压遍数结束，否则，转到步骤（2）继续。

在步骤（1）中，网格化时方格尺寸取值的大小，需要从碾压遍数计算速度以及图形显示方面进行综合考虑。方格取得较大（大于1.0m）时，由于方格数量较少，因而计算量也较小，速度较快，但是遍数图比较粗糙，无法分辨碾压带间的重叠区域；方格取得较小（小于0.1m）时，由于方格数量较大，因而计算量也较大，速度较慢，但是遍数图比较精细，可分辨碾压带间的重叠区域。系统软件最终选取方格大小为0.1m。

在步骤（2）中，没有采用连续的两个采样时刻的振动轮位置生成四边形，而是采用满足一定条件的ti和tj，它们之间可能相差几个采样周期（即几秒），一方面可防止连续的两个采样时刻内碾压机械行驶的距离太小（如速度小于0.36km/h时，距离小于0.1m），使得确定的S′内无法搜索到方格，导致S区域内的遍数少计算1次；另一方面由于减少了四边形总数，加快了计算速度。条件②中d0须综合上述两方面的考虑来确定，软件中取1.5m，但不一定是绝对最佳值。

在步骤（4）中，由于网格化时已将方格取得比较小，判断一个方格是否在S内，通常是判断该方格的中心点是否在S内，若成立则认为该方格在S内。判断点是否位于四边形内是计算碾压遍数的关键。

碾压遍数计算完后，以遍数图的形式显示遍数（将整个碾压区域内每个方格填充与遍数相对应的颜色，即生成遍数图）。由于对碾压机械运动轨迹的简化（假设1个采样周期内为直线运动，而实际是复杂的曲线运行）以及网格法计算碾压遍数的误差（假设方格中心点位于S内则认为该方格位于S内），必然存在少数方格，其计算遍数与实际遍数有一定偏差，与其周围点的遍数有突变，即不平滑，在遍数图中表现为“杂点”（孤立点）。因此，在计算完碾压遍数后，有必要对遍数进行平滑以消去或减少“杂点”。