使用1stOpt软件进行模型参数识别：优化方法

对于实际工程而言，深部洞室围岩劈裂破坏现象出现的判据可以具体化，经过试算，微裂隙起始角度对判据影响较小，因此可以取θ=45°，摩擦系数取μ=0.5，K_IC=0.91MN·m^-3/2，而裂纹的长度量级，模型试验结束后，将模型切开，测量裂缝的尺寸大致为10～15cm，结合模型相似比，换算成真实的工程中，大致为5～7.5m，可引用李晓静[184]博士论文中裂纹长度为5m等级的劈裂判据，即

σ_s1≥2.20+σ_x×10.25 （8-15）

李晓静^[185]论文中对于锦屏一级水电站的地下洞室发生劈裂现象时的模拟结果如图8-7所示。

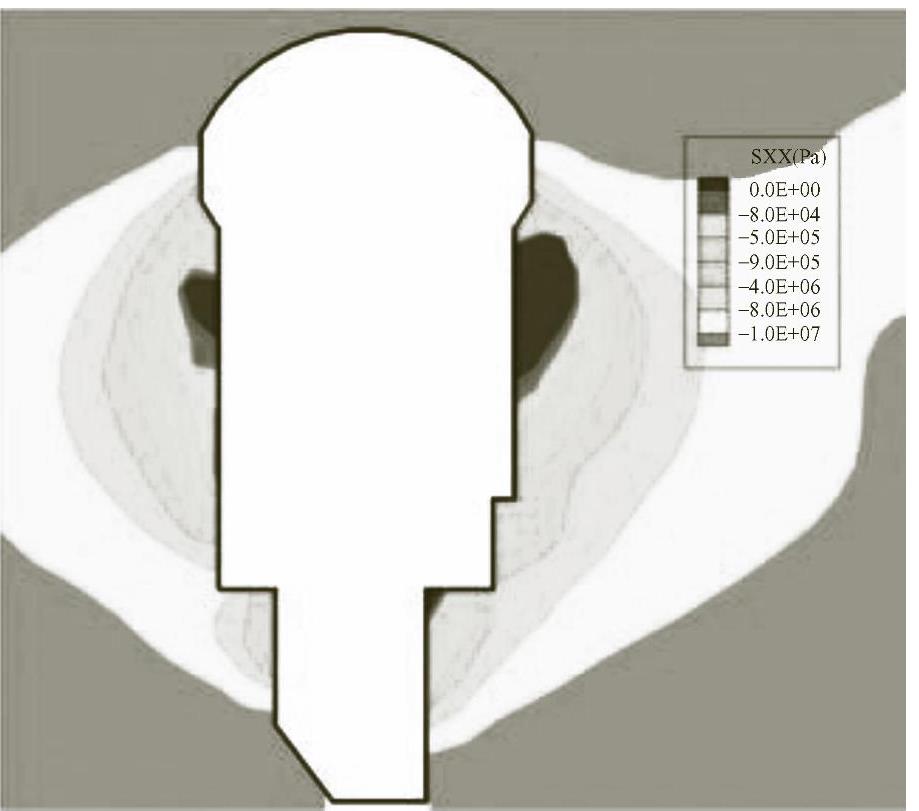
图8-7 开挖卸荷后洞室围岩x方向应力云图

分析可得：深部洞室开挖后，围岩出现劈裂现象时，靠近洞室2号测点周边x方向应力值在0.5MPa左右，远离洞室6号测点周边x方向应力值为4MPa左右（测点号布置见图7-16）。

由分析试验数据可得：

在2号测点，工况一条件下，当围岩x方向应变ε=50×10^-6时，围岩应变开始发生突变，认定此时围岩出现劈裂现象，此时σ_x=ε·E=（50×10^-6×12950）MPa=0.65MPa，而σ_s1≥（2.20+0.65×10.25）MPa=8.86MPa；根据模型相似比1∶50，则模型中σ_s1≥（8.86/50）MPa=0.18MPa。

工况四条件下，当围岩x方向应变ε=80×10^-6时，围岩应变开始发生突变，认定此时围岩出现劈裂现象，此时σ_x=ε·E=（80×10^-6×12950）MPa=1.04MPa，而σ_s1≥（2.20+1.04×10.25）MPa=12.9MPa；根据模型相似比1∶50，则模型中σ_s1≥（12.9/50）MPa=0.26MPa。

锦屏一级水电站地下厂房洞室围岩多为大理岩，所测洞室的围岩类别为Ⅱ类，岩石具有坚硬的质地，它的完整系数达到了K_v=0.923，属于块状结构，其出现风化的程度为微新，大理岩原岩的变形模量接近E₀=20GPa，当开挖结束后，由于引起损失，岩体变形模量变为E=10GPa左右，岩石的泊松比ν=0.25，其断裂韧度达到K_IC=0.91MN·m^-3/2。根据工程地质勘查报告的描述，再结合Song等^[186]对类似岩体中微裂纹的分析结果，并利用反馈分析的方法得到的围岩新参数，继续进行分析进而获取微裂的纹相关参数，见表8-1。

表8-1 锦屏一级水电站地下厂房洞室大理岩微裂纹参数表

将表8-1的数据代入下列式子

所以，有

ε_c=（-4.03×10^-4）σ_z+（8.2×10^-3）σ_x （8-16）

将工况一条件下左边墙的2号点以及工况四条件下右边墙的6号点的应变与时间的关系曲线（测点号布置见图7-16），利用1stOpt软件进行非线性曲线拟合，由于本构方程中的各未知参数形式在软件中输入较为烦琐，所以为方便参数输入，将时效劈裂本构方程变形为

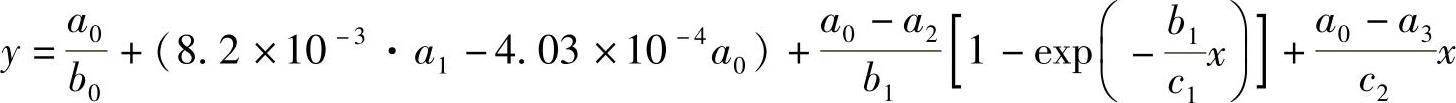
其中，a₀=σ_z，a₁=σ_x，a₂=σ_s2，a₃=σ_s3；b₀=E₀，b₁=E₁；c₁=η₁，c₂=η₂；y=ε；x=t。

1.Ⅱ-Ⅱ截面工况一条件下左边墙2号点

（1）1stOpt软件输出结果

1）编写的代码如下：

Parameters a（0：3），b（0：1），c（0：1）；

Variable x，y1，y2；

Function

if（a0＞=a3，（a0/b0）+（a1∗8.2∗10^（-3）-a0∗4.03∗10^（-4））+（a0-a2）∗（1-exp（-b1∗x/c1））/b1+（a0-a3）∗x/c2，（a0/b0）+（a1∗8.2∗10^（-3）-a0∗4.03∗10^（-4））+（a0-a2）∗（1-exp（-b1∗x/c1））/b1）；

data；

2）工况一条件下左边墙2号点的试验与软件拟合的应变与时间的关系曲线如图8-8所示。

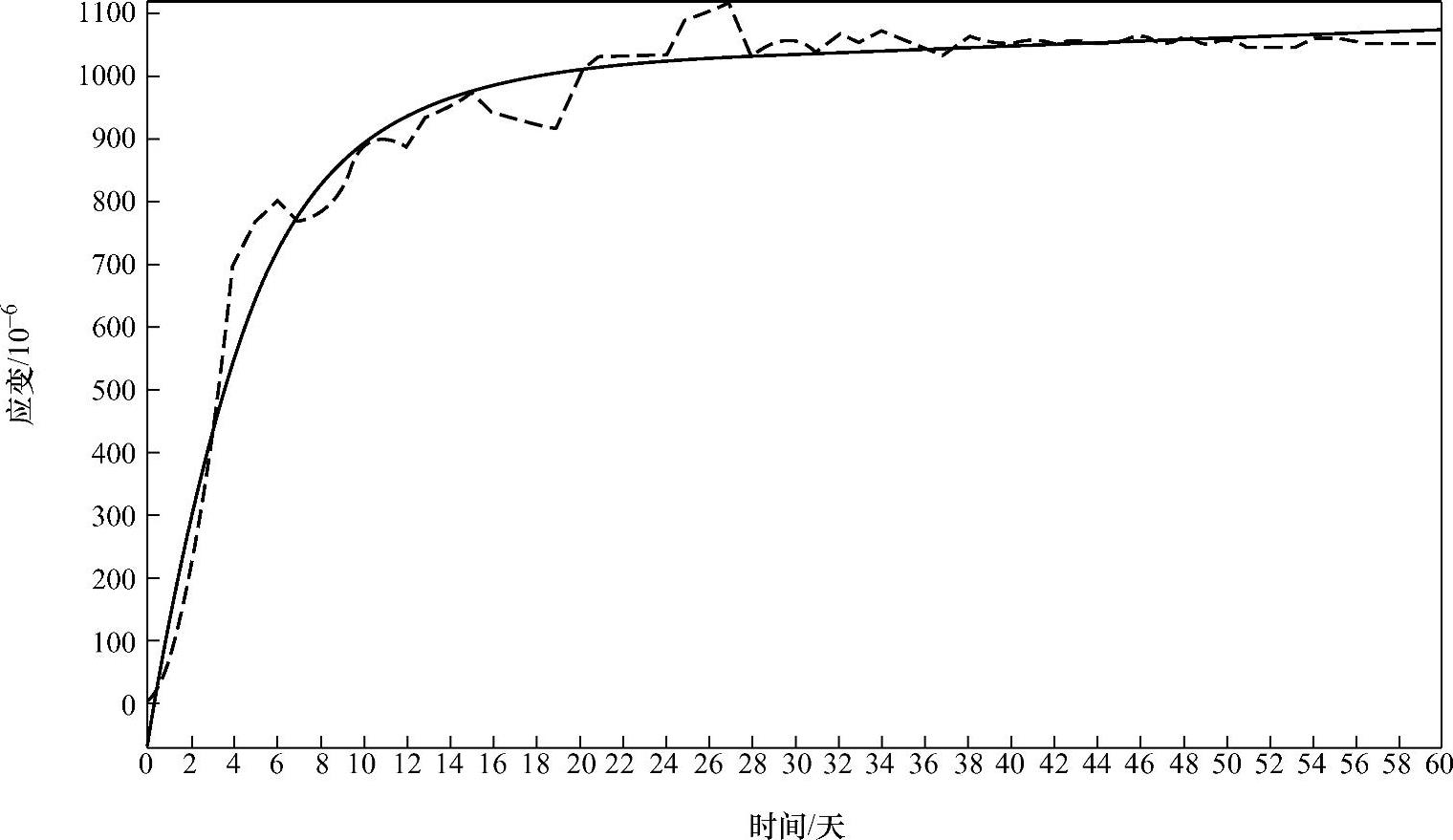
图8-8 试验与软件拟合的应变与时间的关系

3）迭代数：37

计算用时（时：分：秒：微妙）：00：00：10：512

优化算法：麦夸特法（Levenberg-Marquardt）+通用全局优化法

计算结束原因：达到收敛判断标准

均方差（RMSE）：35.651354676066

残差平方和（SSE）：77532.1645047345

相关系数（R）：0.987537223217815

相关系数之平方（R^2）：0.975229767240753

决定系数（DC）：0.975229767240753

卡方系数（Chi-Square）：16.8679690960304(www.xing528.com)

F统计（F-Statistic）：2322.891222963

4）参数及最佳估算见表8-2。

表8-2 参数最佳估算表

5）结果输出见表8-3。

表8-3 结果输出表

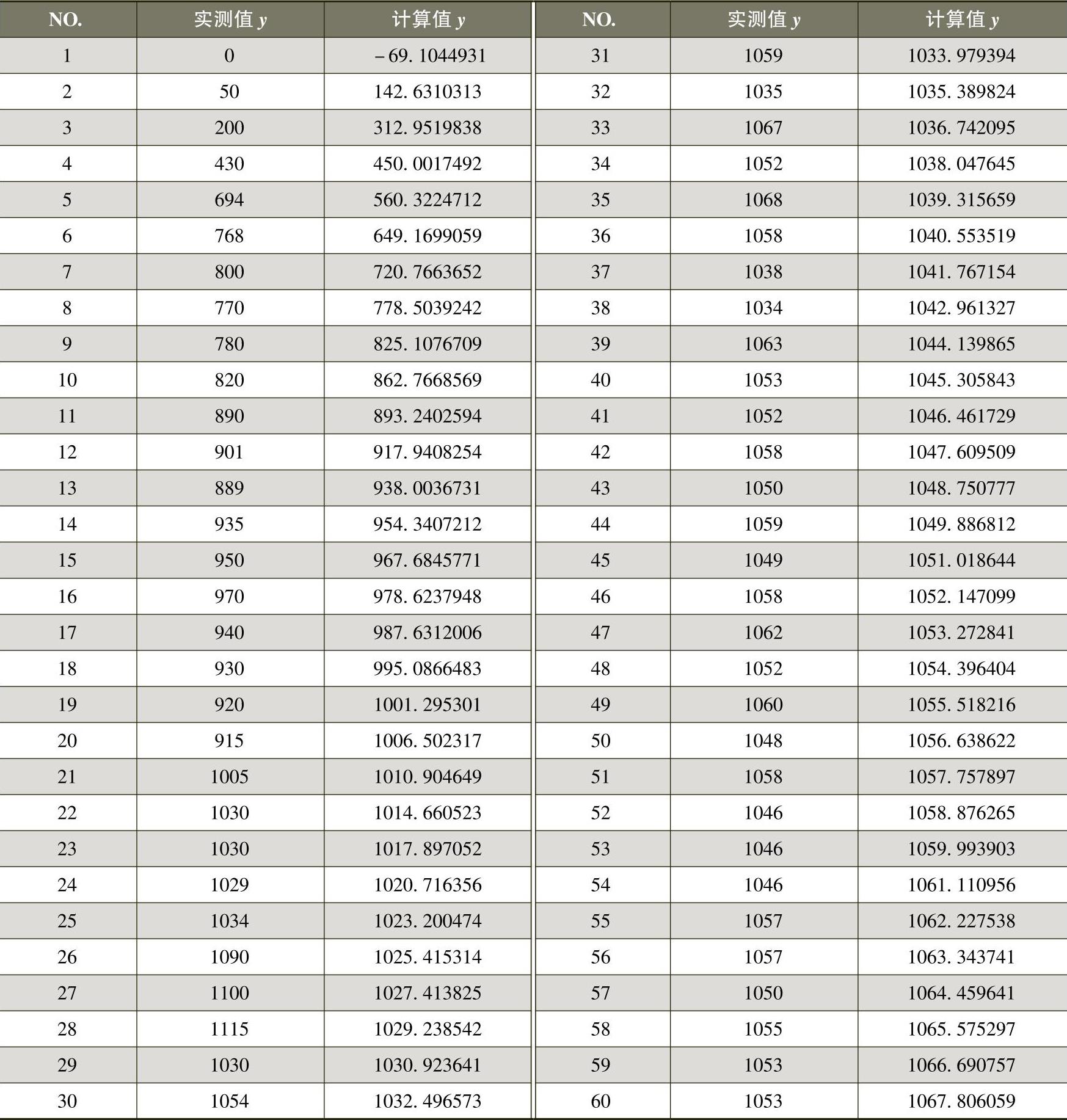
（2）1stOpt软件输出结果分析 首先分析软件模拟出的曲线图（见图8-8），实线是软件模拟出的曲线，而虚线则是通过试验所得到的真实的曲线，软件模拟出的曲线显得更加的平顺，而试验曲线则显得不规整，比较明显的不规整的部分大概出现在岩石劈裂现象出现时效性的前期（即岩石出现蠕变的第一阶段），在这个阶段与模拟曲线区别比较明显，从曲线上来看，主要是从第6天开始到第26天的范围内，而其他阶段虽有区别，但是区别相对较小，但是，总的来看两条曲线的趋势是一致的；接下来再分析参数的最佳估算值，软件对于本构方程中出现的参数进行了估算赋值，总体来看，所赋的数值在合理的范围之内，但也有极个别的数据可能偏差稍微有点大，还需要做进一步的研究，例如弹性模量E₁=0.791568976490805 GPa，结合工程实际，此时的弹性模量值大致应在10GPa左右；最后则是曲线的实测值与计算值的对比，这类似于曲线的对比，同样也是在第6天到第26天的范围内，差距比较明显，例如第6天的实测值为768×10^-6，计算值达到了667×10^-6，两者相差101×10^-6，而第40天的实测值为1053×10^-6，计算值为1045×10^-6，相差仅仅为8×10^-6，但是曲线的总体趋势是一致的。

2.Ⅲ-Ⅲ截面工况四条件下右边墙6号点

（1）1stOpt软件输出结果

1）编写的代码如下：

Parameters a（0：3），b（0：1），c（0：1）；

Variable x，y；

Function

if（a0＞=a3，（a0/b0）+（a1∗8.2∗10^（-3）-a0∗4.03∗10^（-4））+（a0-a2）∗（1-exp（-b1∗x/c1））/b1+（a0-a3）∗x/c2，（a0/b0）+（a1∗8.2∗10^（-3）-a0∗4.03∗10^（-4））+（a0-a2）∗（1-exp（-b1∗x/c1））/b1）；

data；

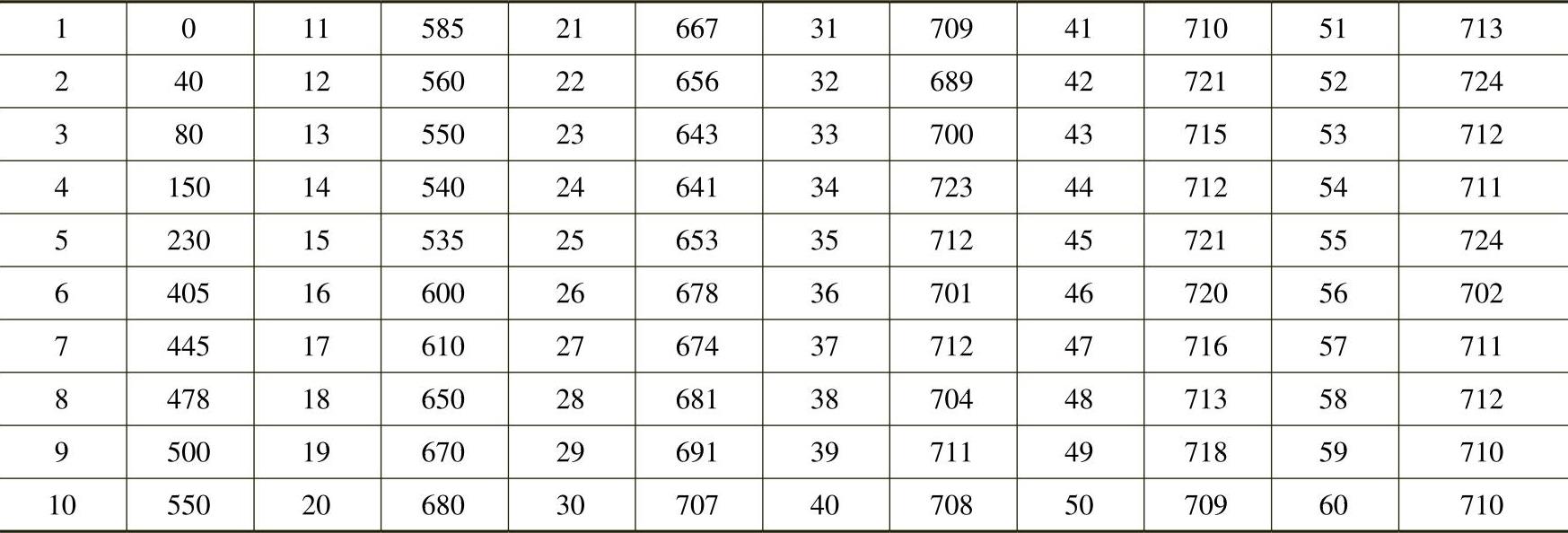
2）工况四条件下右边墙6号点的试验与软件拟合的应变与时间的关系曲线如图8-9所示。

3）迭代数：34

计算用时（时：分：秒：微秒）：00：00：08：391

优化算法：麦夸特法（Levenberg-Marquardt）+通用全局优化法

计算结束原因：达到收敛判断标准

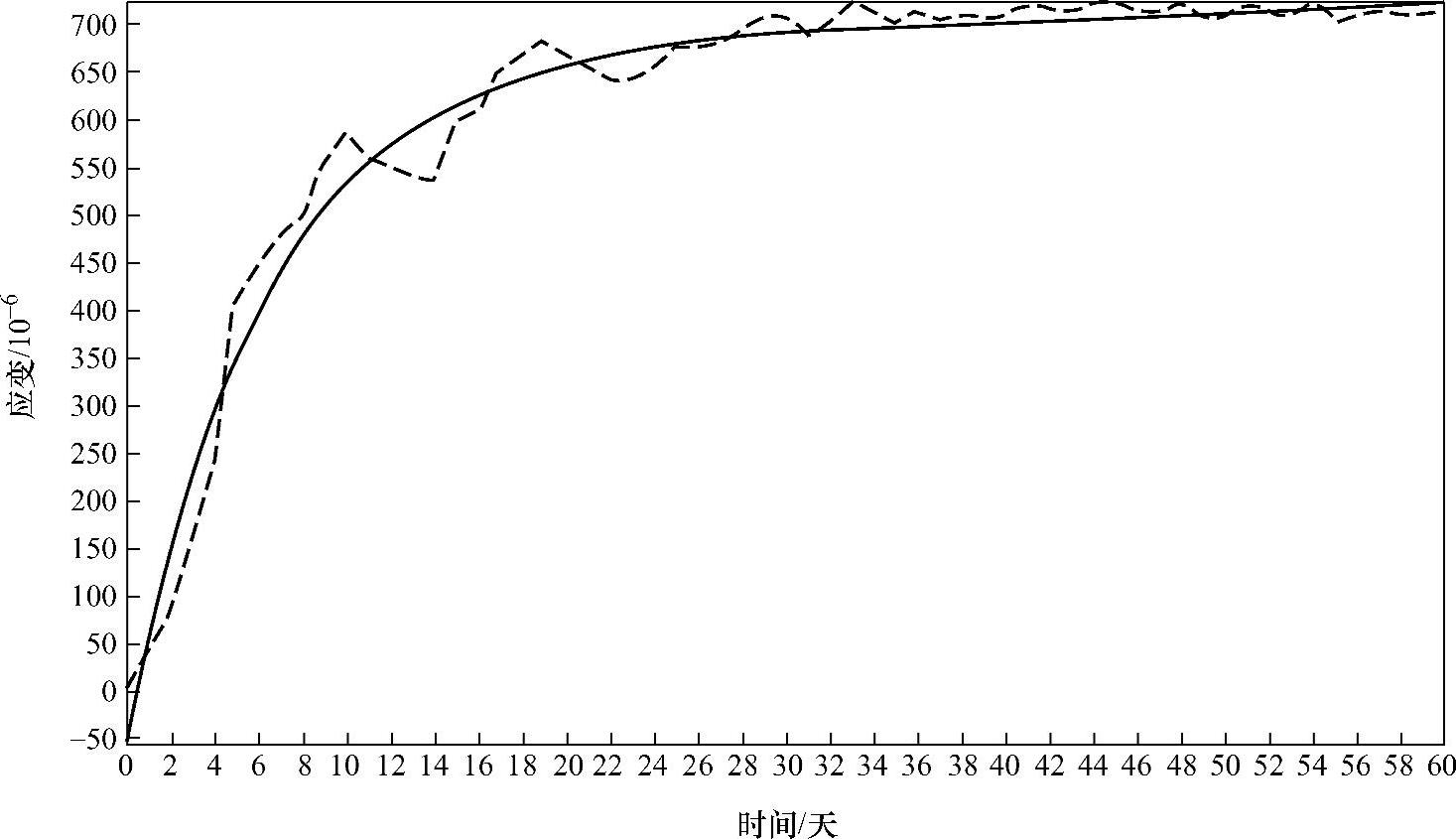
图8-9 试验与软件拟合的应变与时间的关系曲线

均方差（RMSE）：27.1430773101248

残差平方和（SSE）：44941.5453976681

相关系数（R）：0.9875975754278806

相关系数之平方（R^2）：0.975345373869523

决定系数（DC）：0.97523472849202

卡方系数（Chi-Square）：8.69756769782977

F统计（F-Statistic）：2334.06001590782

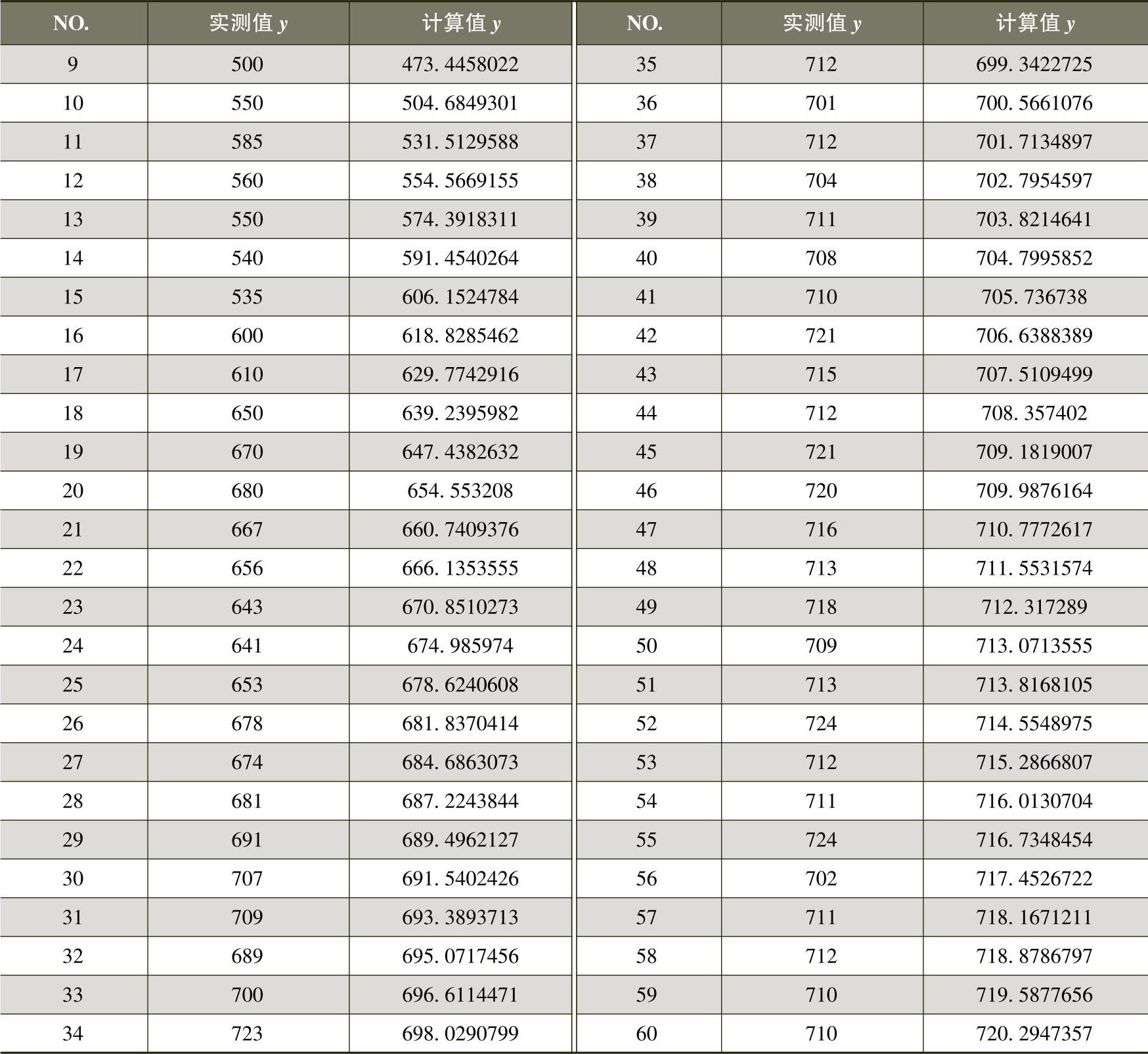
4）参数及最佳估算见表8-4。

表8-4 参数及最佳估算表

5）结果输出见表8-5。

表8-5 结果输出表

（续）

（2）1stOpt软件输出结果分析 如2号点分析软件模拟出的曲线图（见图8-9），实线是软件模拟出的曲线，而虚线则是通过试验所得到的真实的曲线，软件模拟出的曲线显得更加的平顺，而试验曲线则显得不规整，比较明显的不规整的部分大概出现在岩石劈裂现象出现时效性的前期（即岩石出现蠕变的第一阶段），在这个阶段与模拟曲线区别比较明显，从曲线上来看，主要是从第4天开始到第20天的范围内，而其他阶段虽有区别，但是区别相对较小，但是，总的来看两条曲线的趋势是一致的；接下来再分析参数的最佳估算值，软件对于本构方程中出现的参数进行了估算赋值，总体来看，所赋的数值在合理的范围之内，但也有极个别的数据可能偏差稍微有点大，还需要做进一步的研究，例如弹性模量E₁=2.23141723185722GPa，而实测弹性模量大致为E₁=10GPa；最后则是曲线的实测值与计算值的对比，这类似于曲线的对比，同样也是在第4天到第20天的范围内，差距比较明显，例如第6天的实测值为405×10^-6，计算值达到了337×10^-6，两者相差68×10^-6，而第33天的实测值为700×10^-6，真实值为700×10^-6，相差为0，但是曲线的总体趋势是一致的。