建立时效劈裂模型的优化策略

锦屏一级水电站地下洞室围岩的时效劈裂破坏过程：

1）在开挖洞室时洞室周边的围岩出现卸荷，如8.1节所述洞室围岩产生应力的重分布，洞室围岩由三维受压状态调整为两维受压、一维受拉状态，洞室周边围岩在拉应力的作用下发生变形，首先出现短暂的瞬时弹性变形，由于硬质岩石的特性，瞬时塑性变形表征不明显，可以忽略。

2）在高地应力以及围岩卸荷的作用下，当洞室周边围岩中裂隙边缘的应力量值大于围岩劈裂破坏现象发生的门槛值时，围岩中的微裂隙汇总并沿着平行洞室边墙的方向开裂产生劈裂裂缝，围岩出现劈裂现象。随着应力的重新分布过程结束，竖向裂缝的扩展也结束，劈裂现象最终停止，裂缝的尺寸稳定在一个固定的量值附近。

3）虽然围岩卸荷过程结束，在高地应力的持续作用下，围岩中的劈裂裂缝持续扩展，即劈裂现象出现了时效性。岩石出现一部分随时间而增大的应变，此时岩石的应变速率将随着时间的增加而逐渐减小，曲线呈现下凹型，并且向直线状态过渡。

4）随着时间的推移，应变与时间的关系接近于直线变化，应变速率是一个常数，裂缝的宽度以及长度都在缓慢地增加。但是该裂缝并未一直持续扩展下去，最终劈裂裂缝的尺寸稳定在一个固定的数值附近，而并未出现加速蠕变破坏现象。

鉴于上述分析，选用图8-6所示作为深埋洞室围岩的时效劈裂模型，该模型由描述岩石瞬时弹性行为的虎克体、描述岩石劈裂现象的劈裂塑性体、描述劈裂时效性的村山体以及Bingham模型组成。

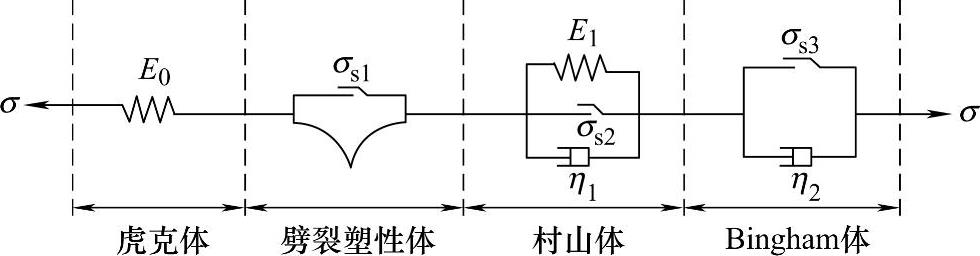
图8-6 洞室围岩的时效劈裂模型(www.xing528.com)

以下进行详细的分析：

1）深部洞室围岩在高地应力条件下发生变形，首先是出现短暂的瞬时弹性变形，可用虎克体来描述该过程出现的瞬时弹性应变，而对于瞬时塑性变形，由于洞室围岩是大理岩，而大理岩属于硬质岩石，在其变形过程中，瞬时塑性变形非常短暂，且变形量非常小，因此可以忽略；然后，在围岩经历了短暂的瞬时弹性变形之后，当围岩中微裂隙的应力值达到产生劈裂现象的门槛值时，围岩发生劈裂破坏现象，用劈裂塑性体来表征该过程出现的劈裂张开应变；接着，随着围岩卸荷过程结束，围岩中的应力重分布现象也渐渐完成，此时由于围岩持续受到地应力的作用，当地应力水平达到一定量值时，围岩的劈裂裂缝继续扩展，出现了时效性，劈裂时效性分两个阶段：第一阶段瞬态变形阶段以及第二阶段稳定破坏阶段。

2）Kelvin体和村山体都可以描述岩石时效劈裂现象的第一个阶段——瞬态变形阶段（即瞬态蠕变阶段），而区别在于Kelvin体在任意小应力作用下都能产生时效破坏变形，没有应力阀值（应力阀值的定义为当围岩受到的应力量值小于某一个值时，围岩不发生变形，只有当受到的应力量值达到该值时，围岩才会出现变形，这个值便被称为应力阀值。），而大理岩属于硬脆性岩石，在低应力状态下，不会出现时效劈裂的现象，因此利用Kelvin体描述与工程实际不符合。而村山体中包含着应力阀值，只有当应力达到阀值以上劈裂现象才产生时效性，与实际情况相符合。

3）能够描述岩石时效劈裂破坏现象的稳定破坏阶段（即稳态蠕变阶段）的模型有Bur_- gers模型和西原模型。

Burgers模型是由马克思威尔模型（M体）与Kelvin模型（K体）串联组成的结构模型。在岩石力学中采用的五元件西原模型，该模型为一个宾厄姆体（Bingham：理想刚塑性体和牛顿流体）与一个Kelvin体串联而成。

Burgers模型由于含有黏性元件，能描述黏性定常流动，但是由于没有屈服极限无法描述岩石长期强度以上的时效劈裂规律，且该模型中的不可恢复变形完全是由黏性流动所致。西原模型中包含的Bingham体，可以描述长期强度以上的时效劈裂稳定破坏阶段，且变形是黏塑性，而不单单是黏性流动。所以选择用Bingham模型来模拟稳定破坏阶段。

4）模型试验以及工程现场数据表明围岩均未出现由于时效劈裂破坏而最终出现失稳破坏的现象，因此时效劈裂破坏现象的三个阶段只出现了前两个阶段：瞬态破坏阶段和稳定破坏阶段。因此该情况下的大理岩时效劈裂破坏模型便可以采用弹性体、劈裂塑性体、村山体以及Bingham模型串联而成。