模型边墙位移和应变变化规律

1.开挖结束稳定状态和时效劈裂试验最终结束状态的位移和应变变化规律

在工况一、二、四条件下，在模型体中布置3个监控断面记录应变与位移的变化（见图7-15），监测元件的安排如图7-16、图7-18和图7-19。在试验过程中，利用数据采集系统记录边墙各测点的侧向应变和侧向位移的测试数据。表7-7和表7-8给出了开挖结束后稳定状态下和时效劈裂试验最终结束时洞室边墙各测点的侧向位移和侧向应变，将开挖结束稳定状态作为初始状态，将时效劈裂试验最终结束状态作为最终状态。然后处理数据，得到边墙侧向位移、侧向应变的变化图，如图7-26和图7-27所示。

表7-7 工况一、二、四下模型边墙各测点的侧向位移

（续）

表7-8 工况一、二、四下模型边墙各测点的侧向应变

注：侧向应变数值为正值表示拉应变。

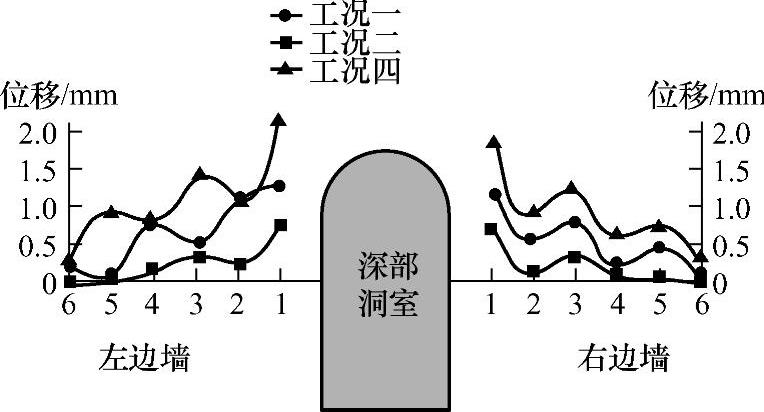
图7-26 工况一、二、四下模型边墙各测点最终状态下侧向位移变化示意图

图7-27 工况一、二、四下模型边墙各测点最终状态下侧向应变变化示意图

a）应变测试断面Ⅱ-Ⅱ b）应变测试断面Ⅲ-Ⅲ

由模型边墙破坏情况所监测的数据分布图（见图7-27）可知：

1）三个工况条件下，边墙测点的侧向位移和侧向应变曲线均呈现出类似波形，即曲线有峰值有低谷并且交替分布的变化规律，监测数据较大的峰值部位是围岩劈裂破坏区，较小的波谷部位为未破坏区，测的试验数据与模型边墙的破坏情况吻合（见图7-21、图7-22和图7-25），因此测试数据和边墙的破坏分布印证了劈裂现象的出现。

2）在洞室开挖结束之后，维持原加载状态，三种工况条件下的模型中的监测元件均监测到了围岩中各测点的位移和应变的增加，表明了在这种应力状态下，围岩的劈裂破坏现象出现时效性。

3）分析各自的数据，发现工况一的数据大于工况二，所以最大加载应力值对劈裂破坏现象影响很大，并且值越大，边墙的侧向位移和侧向应变越大，时效劈裂破坏现象越明显；工况四的数据大于工况一，因而垂直洞室方向的应力值对劈裂破坏现象影响也很大，且值越大，边墙的侧向位移和侧向应变越大，时效劈裂破坏现象也越明显。

4）监测断面中测点距洞室越近，其侧向位移越大，侧向应变也越大，这说明接近洞室的范围是传统含义中的松动圈；相反距离越远侧向位移越小，侧向应变也越小，最远测点值接近于零，表明该点处于破坏的边界位置。

2.时效劈裂试验中蠕变位移增量和蠕变应变的变化规律

表7-7和表7-9给出了蠕变位移和应变的增量，蠕变增量是以时效劈裂试验为最终状态下的位移和应变值与开挖结束稳定状态下的位移和应变值的差来确定。图7-28和图7-29为工况一、二、四下洞室边墙位移和应变的蠕变增量的变化图。

表7-9 工况一、二、四下模型边墙各测点的侧向应变的蠕变增量

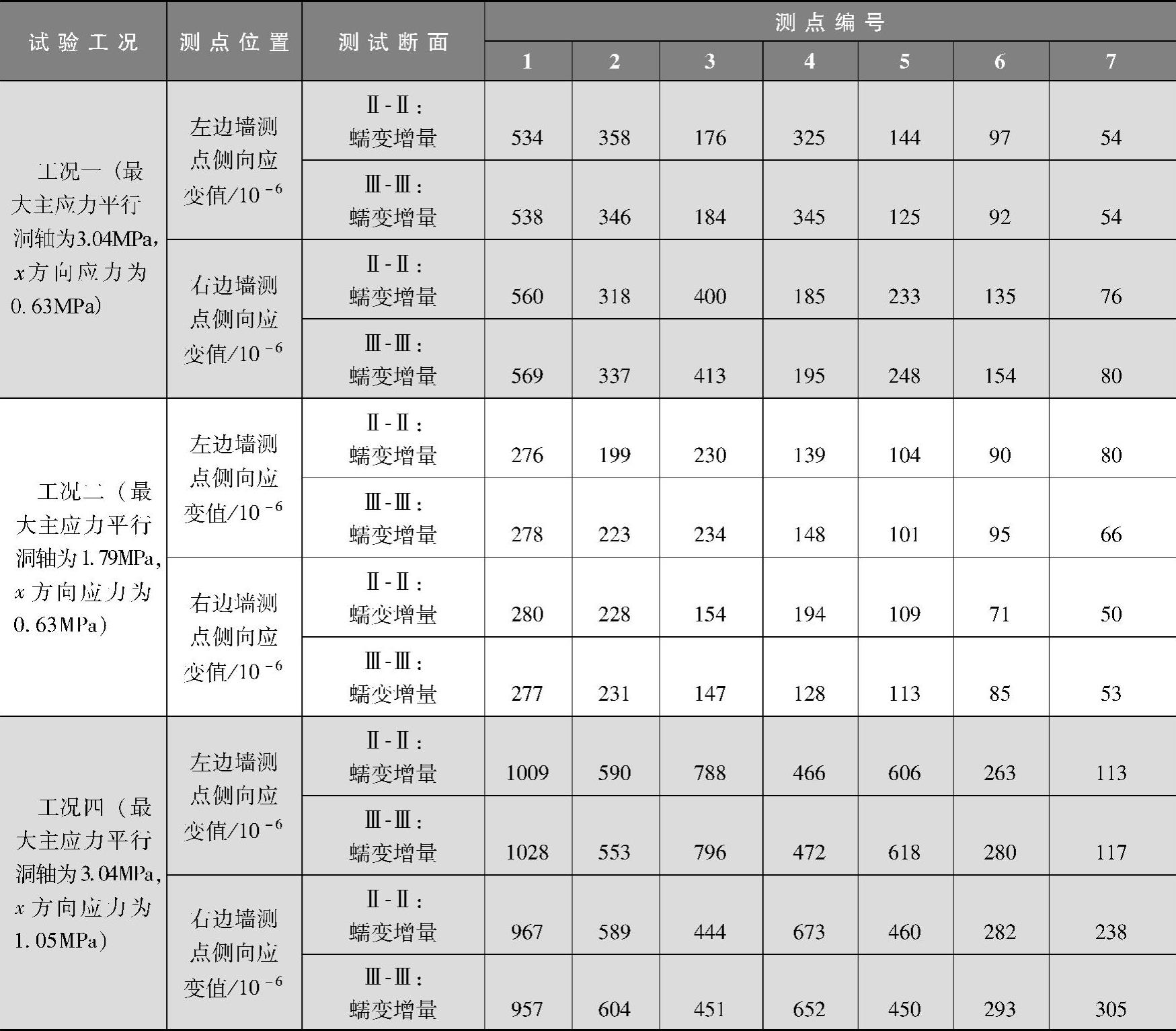
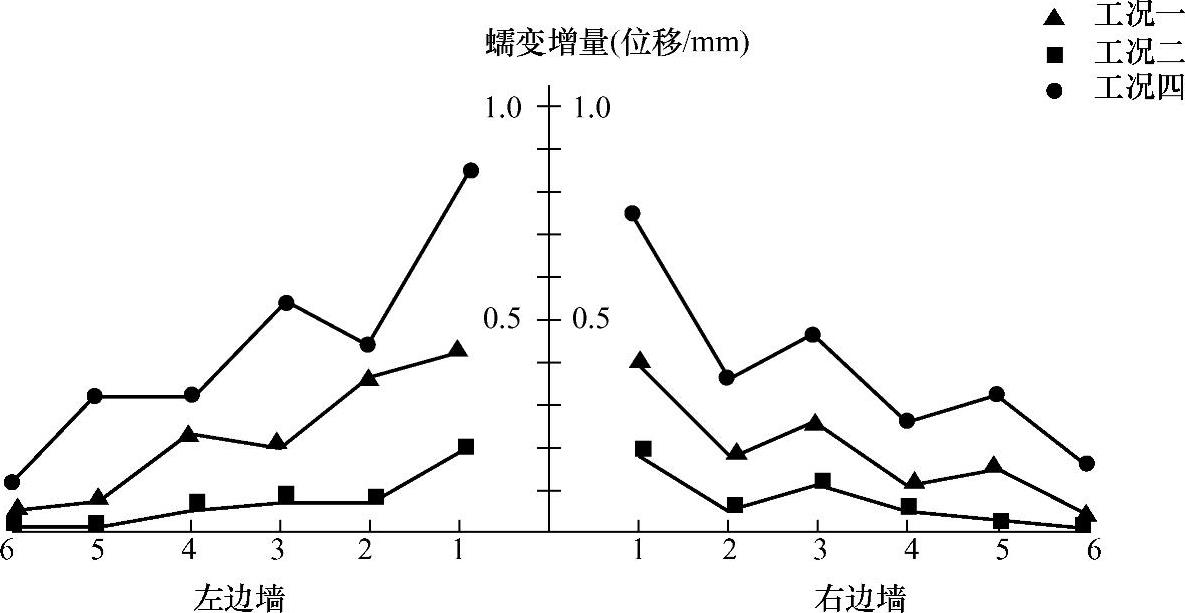
图7-28 工况一、二、四下模型边墙各测点侧向位移蠕变增量变化示意图

图7-29 工况一、二、四下模型边墙各测点侧向应变蠕变增量变化示意图(www.xing528.com)

a）Ⅱ-Ⅱ断面 b）Ⅲ-Ⅲ断面

分析上述蠕变增量表格以及变化示意图可知：

（1）三种工况下的蠕变增量大小有所差异 对比工况一和工况二条件下模型试验的蠕变增量，明显可以看到不论是位移的蠕变增量曲线，还是Ⅱ-Ⅱ断面和Ⅲ-Ⅲ断面的应变蠕变增量曲线，工况一条件下的模型蠕变增量曲线都在工况二条件下模型蠕变增量曲线之上，说明工况一条件下蠕变增量要大于工况二条件下的蠕变增量，表明最大主应力越大，围岩的时效劈裂现象越明显；对比工况一和工况四条件下模型试验的蠕变增量，也可看到不管是位移的蠕变增量曲线，还是Ⅱ-Ⅱ断面和Ⅲ-Ⅲ断面的应变蠕变增量曲线，工况四条件下的模型蠕变增量曲线都在工况一条件下模型蠕变增量曲线之上，说明工况一条件下蠕变增量要大于工况二条件下的蠕变增量，表明垂直洞室方向应力越大，围岩的时效劈裂现象越明显。

（2）三个工况条件下的模型蠕变增量曲线的趋势是相同的，也是呈现出了波峰波谷交替出现的情形，并且沿着洞室边墙越往里越小。距测试断面中距洞壁最远的测点的侧向位移和侧向应变的蠕变增量均接近于零，表明最远测点已经接近破坏区边缘。

3.选定具有代表性的测点展开分析

左边墙选定2号点，右边墙选定6号点，分析应变的蠕变增量。首先分析三种工况条件下，模型的蠕变增量的情况，见表7-10和表7-11，然后将左边墙2号点和右边墙6号点在整个试验过程中的应变变化的数据进行整理并绘制曲线如图7-30、图7-31和图7-32。

表7-10 Ⅱ-Ⅱ断面岩石开挖结束增量和蠕变增量

表7-11 Ⅲ-Ⅲ断面岩石开挖结束增量和蠕变增量

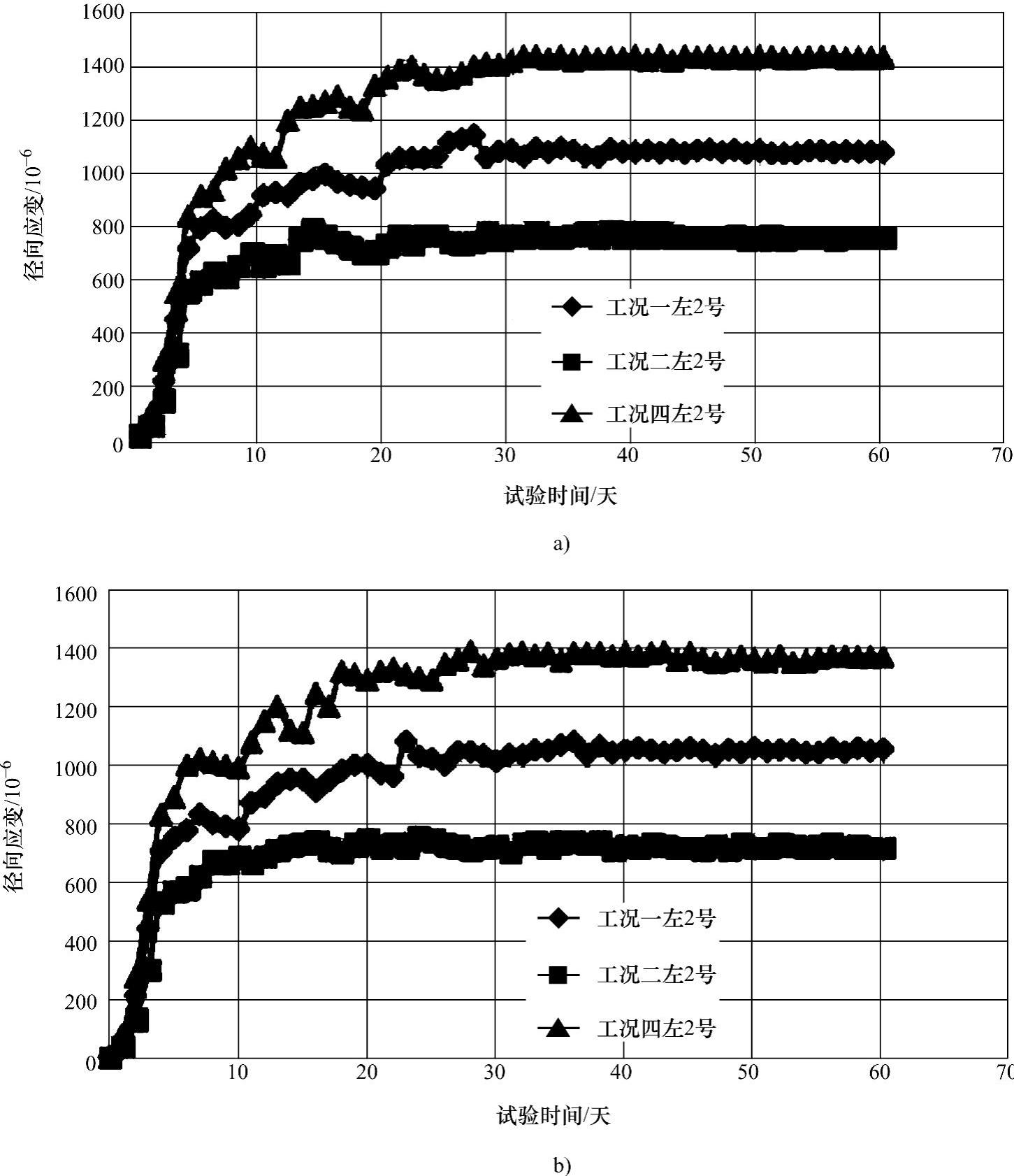
图7-30 各工况下模型左边墙2号测点的应变-时间关系曲线

a）Ⅱ-Ⅱ截面 b）Ⅲ-Ⅲ截面

分析表7-10和表7-11可知：

1）对于左边墙2号测点而言，首先分析Ⅱ-Ⅱ断面的处理数据。对比工况一条件和工况二条件，发现工况一条件下侧向应变的蠕变增量占侧向总应变的比例为34%，而工况二条件下侧向应变蠕变增量占侧向总应变的比例为27%，工况一条件下侧向蠕变增量占侧向总应变的比例比工况二大，即工况一试验的时效劈裂破坏现象要比工况二明显；对比工况一条件和工况四条件，发现工况工况一条件下侧向应变的蠕变增量占侧向总应变的比例为34%，而工况四条件下侧向应变蠕变增量占侧向总应变的比例为41%，工况四条件下侧向蠕变增量占侧向总应变的比例比工况一要大，即工况四试验的时效劈裂破坏现象比工况一要明显。再分析Ⅲ-Ⅲ断面的处理数据：对比工况一条件和工况二条件，发现工况一条件下侧向应变的蠕变增量占侧向总应变的比例为33%，而工况二条件下侧向应变蠕变增量占侧向总应变的比例为26%，工况一条件下蠕变增量占总应变的比例比工况二条件下也要大，即工况一条件下模型试验的时效劈裂破坏现象也要比工况二条件下模型试验的时效劈裂时效现象要明显；对比工况一条件和工况四条件，发现工况一条件下侧向应变的蠕变增量占侧向总应变的比例为33%，而工况四条件下侧向应变蠕变增量占侧向总应变的比例为40%，工况四条件下侧向蠕变增量占侧向总应变的比例比工况一条件下也要大，即工况四条件下模型试验的时效劈裂破坏现象也要比工况一条件下模型试验的时效劈裂时效现象要明显。

图7-31 各工况下模型右边墙6号测点的应变-时间关系曲线

a）Ⅱ-Ⅱ截面 b）Ⅲ-Ⅲ截面

图7-32 Ⅱ-Ⅱ截面工况一条件下2号测点和6号测点的应变与时间关系曲线

2）对于右边墙6号测点而言，首先分析Ⅱ-Ⅱ断面的处理数据。对比工况一条件和工况二条件，发现工况一条件下侧向应变的蠕变增量占侧向总应变的比例为32%，而工况二条件下侧向应变蠕变增量占侧向总应变的比例为25%，工况一条件下侧向蠕变增量占侧向总应变的比例比工况二要大，即工况一试验的时效劈裂破坏现象要比工况二要明显；对比工况一条件和工况四条件，发现工况工况一条件下侧向应变的蠕变增量占侧向总应变的比例为32%，而工况四条件下侧向应变蠕变增量占侧向总应变的比例为42%，工况四条件下侧向蠕变增量占侧向总应变的比例比工况一要大，即工况四条件下的时效劈裂破坏现象要比工况一明显。再分析Ⅲ-Ⅲ断面的处理数据：对比工况一条件和工况二条件，发现工况一条件下侧向应变的蠕变增量占侧向侧向总应变的比例为34%，而工况二条件下侧向应变蠕变增量占侧向总应变的比例为27%，工况一条件下侧向蠕变增量占侧向总应变的比例比工况二条件下也要大，即工况一条件下模型试验的时效劈裂破坏现象也要比工况二条件下模型试验的时效劈裂时效现象要明显；对比工况一条件和工况四条件，发现工况一条件下侧向应变的蠕变增量占侧向总应变的比例为33%，而工况四条件下侧向应变蠕变增量占侧向总应变的比例为43%，工况四条件下侧向蠕变增量占侧向总应变的比例比工况一条件下也要大，即工况四条件下模型试验的时效劈裂破坏现象也要比工况一条件下模型试验的时效劈裂时效现象要明显。

分析图7-30、图7-31和图7-32可知：

1）Ⅱ-Ⅱ截面和Ⅲ-Ⅲ截面在工况一、二、四下的2号和6号测点的应变与时间的关系曲线主要包括三个部分。第一部分开挖卸荷阶段，此阶段持续时间为第1天到第5天，这个阶段的应变呈现直线增长趋势，增长率非常大；第二阶段是瞬态蠕变阶段，此阶段持续时间大概是为第6天到第10天，这个阶段的应变是呈现上凸增长的趋势，即呈现增长率由大到减小的增长趋势；第三阶段稳定蠕变阶段，此阶段的持续时间为第10天到30天，这个阶段最明显的特征就是应变与时间的关系近似直线关系，斜率为一固定的常数，然后当应变值达到一定量值后稳定在这个量值左右，不再产生较大的变化。

2）分析左边墙2号测点的应变与时间的关系曲线。工况一条件下的模型试验曲线在工况二条件下的模型试验曲线之上，表明工况一条件下模型的时效劈裂现象要比工况三条件下模型的时效劈裂现象明显；工况四条件下的模型试验曲线在工况一条件下的模型试验曲线之上，表明工况四条件下模型的时效劈裂现象比工况一条件下的模型的时效劈裂现象明显。同样分析右边墙6号测点的应变和时间曲线：工况一条件下的模型试验曲线在工况二条件下的模型试验曲线之上，表明工况一条件下模型的时效劈裂现象要比工况三条件下模型的时效劈裂现象明显；工况四条件下的模型试验曲线在工况一条件下的模型试验曲线之上，表明工况四条件下模型的时效劈裂现象比工况一条件下的模型的时效劈裂现象明显。

3）对比工况一条件下左边墙2号测点和右边墙6号测点：发现在工况一条件下左边墙2号测点的应变与时间的曲线在右边墙6号测点的应变与时间的曲线之上，说明左边墙2号点时效劈裂现象要比右边墙6号点明显，说明围岩的时效劈裂现象呈现出沿着侧向越往深处越减弱的趋势。