分析二滩工程实例

1.工程地质条件

二滩工程围岩多属于新鲜、坚硬的印支期正长岩和辉长岩以及二叠纪侵入变质的玄武岩。岩质坚硬，岩体完整，结构面破坏微弱，属于高地应力区的脆性岩石材料。无贯穿性的软弱结构面。

岩石的抗压强度较高，其中正长岩为130.5MPa，玄武岩为148.1MPa。岩石的抗拉强度相对较低，正长岩为6.24MPa，玄武岩为8.1MPa。拉压比在1/20左右。变形模量E为30～50GPa。地下工程围岩按照分类标准划分，属于Ⅰ、Ⅱ类岩体的占91%，Ⅲ类岩体的占7%，Ⅳ、Ⅴ类岩体的占2%，从岩体质量评价看，地下工程岩体质量良好。

厂房地下洞室位于构造应力为主，自重应力和构造应力联合作用的高地应力区。在垂直埋深170～190m时，最大主应力值为18.8～38.4MPa；在垂直埋深270～360m时，最大主应力值为22.3～29.5MPa。

2.主要水工建筑物

在二滩工程地下洞室中，也采用了通常采取的三大洞室布置方式即主厂房、主变室及尾水调压室成平行布置，轴向方向N6E，尺寸如下：主厂房（长×宽×高）：280.3m×25.5m×60.5m；主变室（长×宽×高）：199.0m×17.4m×25.0m；尾水调压室（长×宽×高）：203m×19.5m×58.1m；尾水洞室（长×宽×高）：888.1m×16m×16m。

主变室和主厂房及尾水调压室的水平间距分布为35m和30m。整个地下厂房位于距离拱坝左肩约80m，平均埋深250～450m，侧向岩石厚度为300m。图6-1为地下厂房结构布置图。

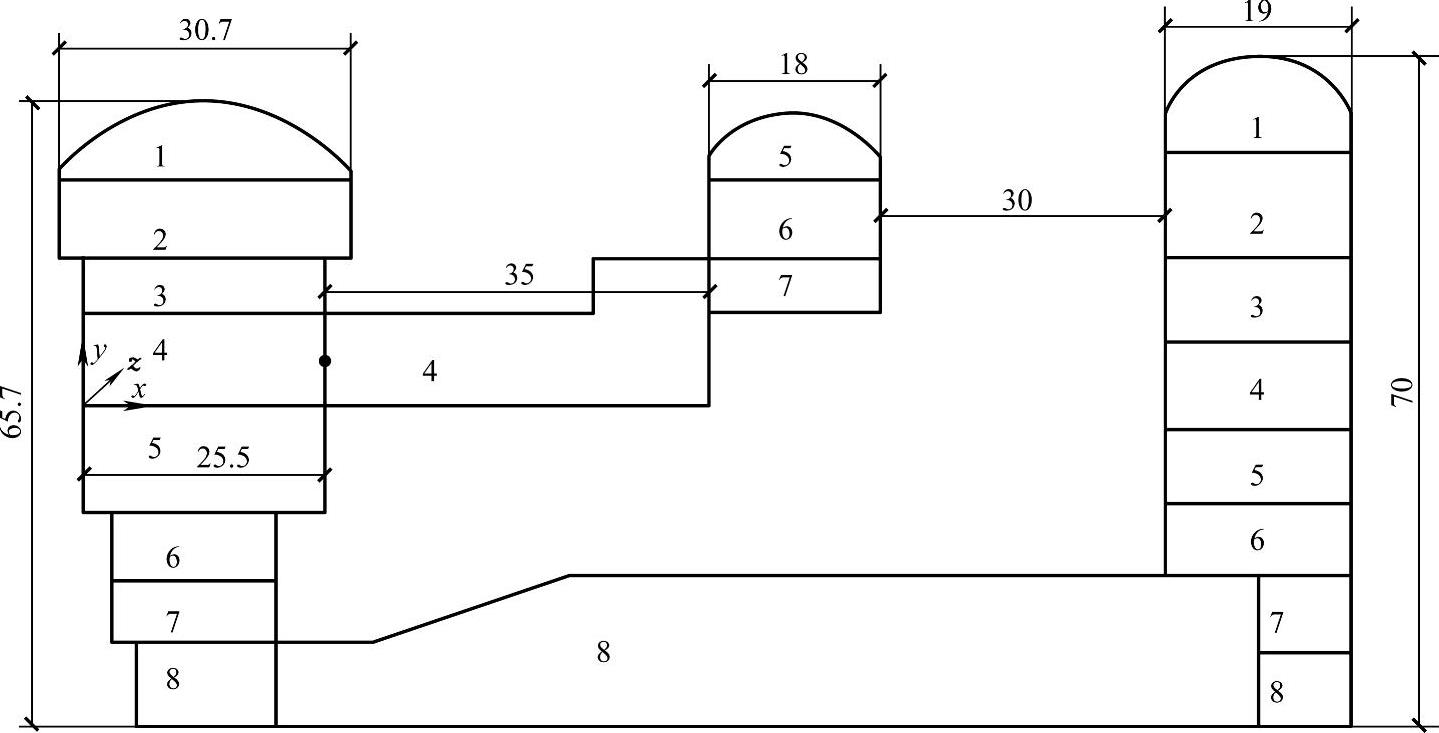
图6-1 二滩工程地下厂房结构布置图（单位：m）

在二滩地下工程中进行了大量的监测工作，取得了许多丰富的观测资料：顶拱变形较小约为2.5mm，最大变形量为14.0mm。边墙中部位移相对较大，量值为55mm左右，最大值为184.6mm（见图6-2）。

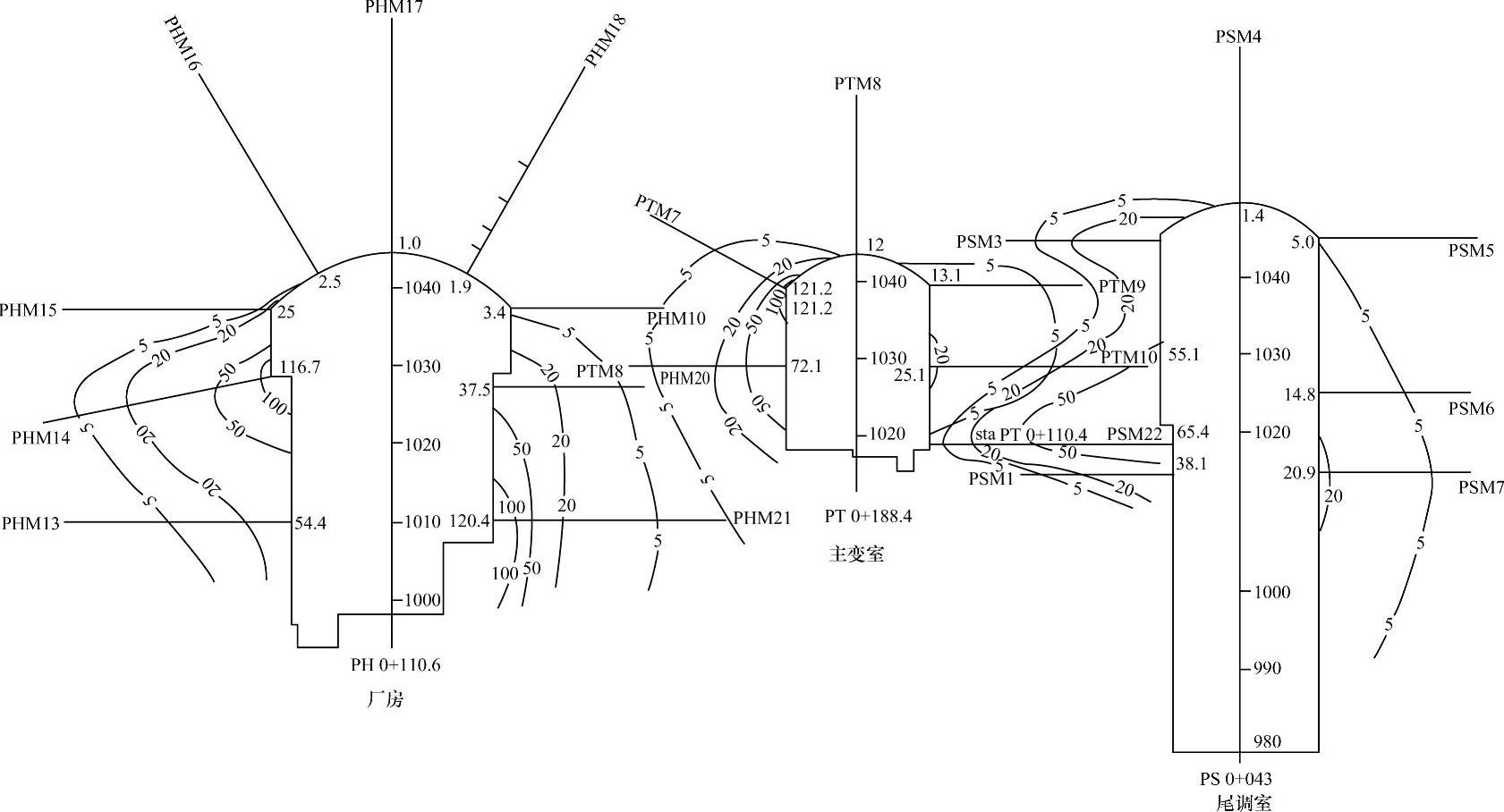
图6-2 工程现场位移监测等值线图

3.数值计算分析

二滩工程地下厂房的规模和所处的岩体结构及地应力环境决定了围岩破坏方式。对开挖跨度达到20m，高度达到60m的地下厂房而言，围岩潜在的首要破坏方式还是以块体破坏。但是，对于顶拱及其与边墙过渡地带、施工过程中不同开挖面之间岩体也可以出现相当高的应力集中现象而导致应力“自励”型破坏。前几章也分析表明，当最大切向应力与岩石单轴抗压强度之比达到0.2或更高时，开挖过程中可以出现比较典型的高应力破坏现象。地下厂房施工过程中的多个洞、多个工作面开挖，可能会很容易使后开挖部位受到先开挖的临近洞室二次应力场的影响，从而满足高应力条件。

一般地，进行高应力条件下的地下工程开挖时，破损区几乎是不可避免的。对于完整脆性岩体而言，塑性区的形成和发展过程通常伴随着应力劈裂裂缝、片帮、爆裂等特殊现象的产生，严重时甚至可以导致足以造成工程危害的地震现象，危及生产和工程的安全。因此，研究破坏区范围内的岩体在开挖过程中的能量变化，进而通过该方法判断岩体的失稳情况，具有实际意义。

4.地下工程围岩参数的确定

二滩水电站地下工程围岩主要以完整的正长岩为主，岩性完整，节理裂隙不发育。围岩强度高，质地脆。其详细参数见表6-1。

表6-1 岩体力学参数表

5.尺寸的确定和网格的划分

本章主要是定性的分析洞室开挖过程的能量变化。因此，简化起见，建立计算模型时只考虑主厂房、主变室及尾水调压室等三大洞室，且不考虑断层等结构面，围岩选取单一岩性。

计算模型取厂房横断面水平方向为x轴，竖直方向为y轴，纵轴线为z轴。计算范围：x方向，-333.05～482.35m，机组轴线为坐标零点；y方向，高程为408.85m处至地表，洞室顶部到地表的埋深为350m；采用准三维模型，即平面模型沿厂房轴线方向取一定厚度，该模型厚度取1m。围岩采用8节点等参单元。

6.本构方程的选取

数值计算中选取FLAC里面的应变软化模型来模拟高地应力作用下硬岩的破裂区[170]。FLAC3D基于三维快速拉格朗日分析方法，采用三维显式有限差分法程序，可以模拟岩土或其他材料构成的地层和结构的三维力学行为。FLAC3D以节点为计算对象，将力和质量均集中在节点上，然后，通过运动方程在时域内进行求解。获得新的运动速度和位移增量。并可以获得某一时步的单元应变增量为

得到了应变增量，由本构方程可求出新的应力增量，叠加后即可得到总应力获得下一时步新应力值，再由虚功原理求出下一时步的节点不平衡力，进入下一时步的计算。

岩石的脆性破坏是岩石受到荷载作用后，大量的微裂纹随着荷载的增大逐渐扩展、连通，当累积到一定程度后产生宏观裂纹的过程。从力学的观点来看，岩石破坏过程是岩石强度逐渐减小或失去的过程。在破坏的初始阶段，微裂纹数量的增多，使微颗粒之间的束缚力减小或失去，从整体层面上造成岩体的黏聚力强度逐渐下降，如图6-3所示。随着微裂纹的扩展、连通直至较大的裂纹形成后，在裂纹面上法向力和剪切力作用下，裂纹面之间摩擦力逐步启动，从整体层面上造成岩体的摩擦强度逐渐上升，最终黏聚力和摩擦强度各自趋于稳定值，如图6-4所示。

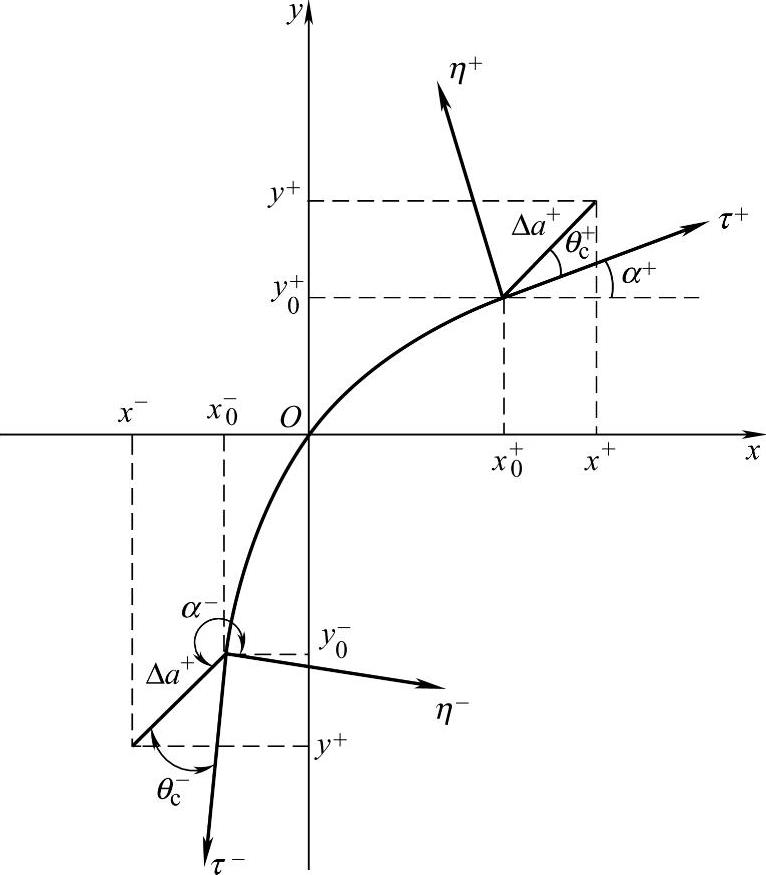
图6-3 裂纹扩展轨迹模型

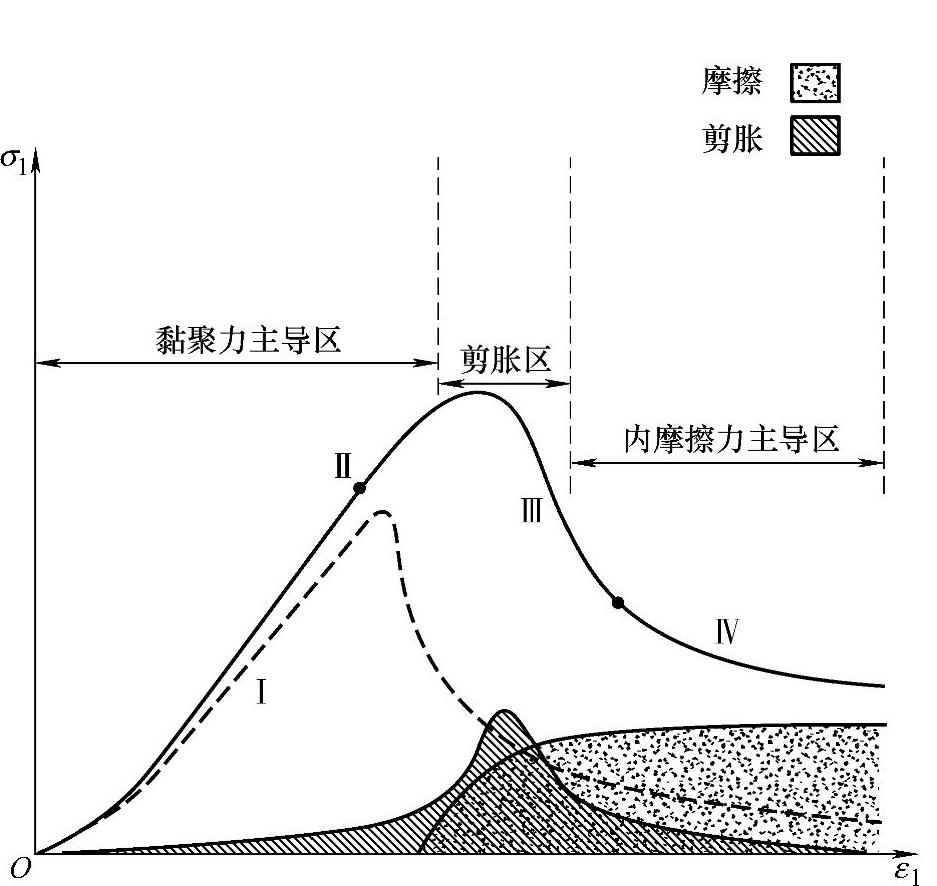
图6-4 应变软化模型

苏国韶等^[171]应变硬化-软化模型主要是基于莫尔-库仑强度准则基础上提出来的，公式如下

τ=ε^p（c+σ_ntanφ） （6-5）

式中 τ——岩体抗剪强度；

σ_n——岩体破坏面上的正应力；

c，φ——岩体的黏聚力和内摩擦角；

ε^p——等效塑性应变。(www.xing528.com)

7.结果分析

原岩在地应力作用下处于平衡状态，地下工程的施工开挖破坏了这种平衡。开挖造成应力释放，使得洞壁围岩的径向应力减小，切向应力增加，且主应力方向发生偏转，最大主应力方向沿洞室切向，最小主应力方向沿洞室径向。对于主厂房来说，由于其边墙部位高度高，应力释放范围大，开挖后洞壁围岩的水平向的第三主应力释放殆尽，甚至部分区域出现了拉应力，正如李天斌等^[172]认为卸荷实质上相当于在原来的应力状态上叠加了一个侧向的拉应力，因此，在边墙部位出现拉应力集中区，计算得出二滩工程地下厂房开挖后，边墙部位的最大拉应力量值为3MPa。另外，机蜗等处的围岩由于多面临空，应力释放剧烈，也容易产生拉应力集中，如图6-5～图6-7所示。边墙部位在开挖后发生以水平位移为主的回弹位移。高地应力情况下，开挖使得大量弹性应变能释放，易造成边墙产生指向洞内的倾倒型破坏；从弹性力学角度分析，边墙由于高度很大，开挖后易形成如前面章节所述的薄板，在切向的集中压应力作用下，容易出现压曲变形从而导致失稳破坏的现象。

本著作计算所得开挖后边墙发生的最大位移为40mm，而顶拱及底板处则有明显的压应力集中，如图6-8所示，且由于拱形结构的良好受力特点，顶拱处一般不会发生大的位移。观察图6-8所示的位移矢量图，可以看出，洞室开挖后主要的变形集中在高边墙处，因此，对于地下厂房来讲，高边墙的稳定性往往是设计者最关心的问题。所以，研究卸载使得边墙产生劈裂裂缝的现象及机理有很重要的现实意义。同时，由图6-8可以看出，主厂房上游边墙的位移要大于下游边墙的位移，这主要是由下游边墙不远处的主变室开挖，它对主厂房下游边墙的变形有牵制作用。

图6-5 主厂房开挖后，洞室周边围岩最大主应力分布图

图6-6 主厂房开挖后，洞室周边围岩最小主应力分布图

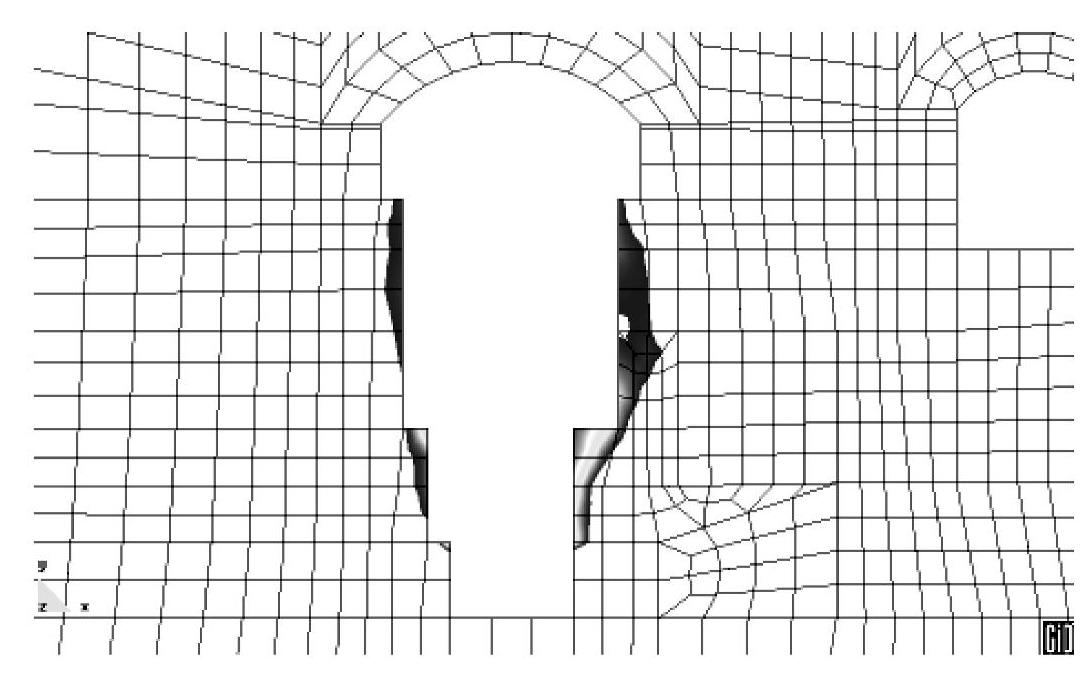
图6-7 主厂房开挖后，洞室周边围岩拉应力分布图

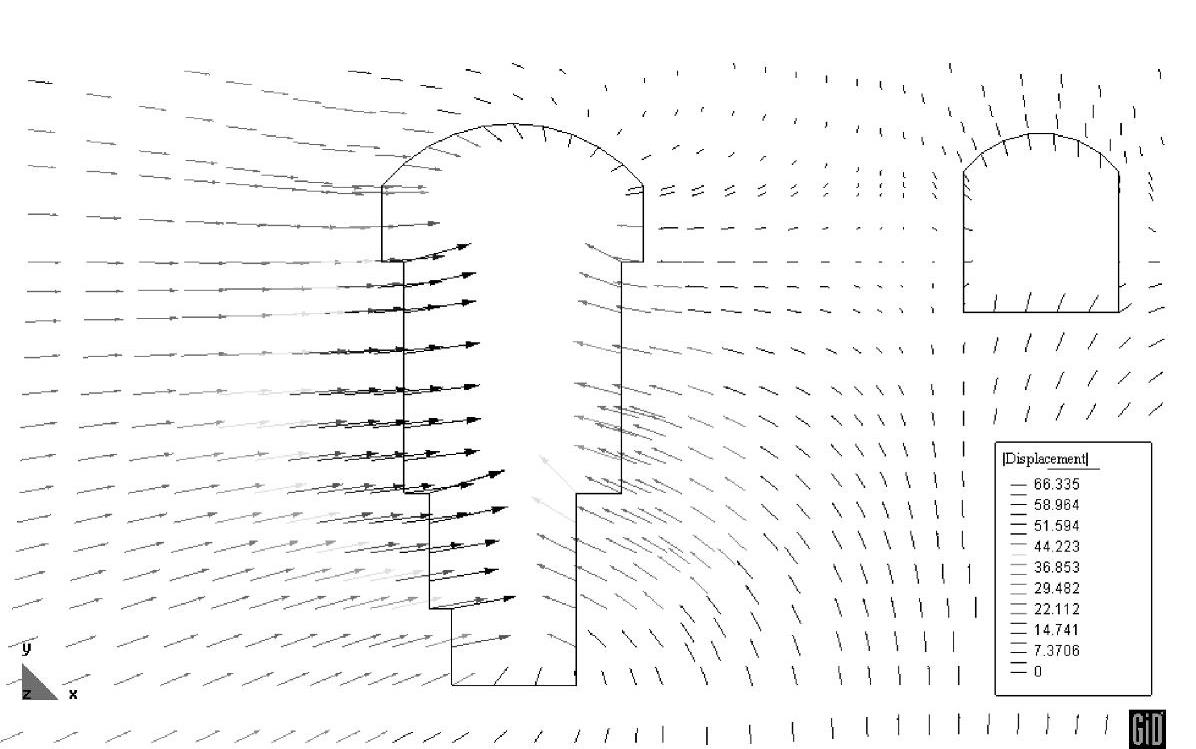
图6-8 主厂房开挖后，洞室周边围岩位移矢量图

结合二滩工程现场观测到的破坏现象，算例中选取主厂房下游边墙到主变室之间的岩柱20m深度。为了分析开挖对围岩不同部位能量变化的影响，选取了6个典型单元进行对比分析，如图6-9所示，1号到6号单元能量随时步变化如图6-10～图6-15所示。

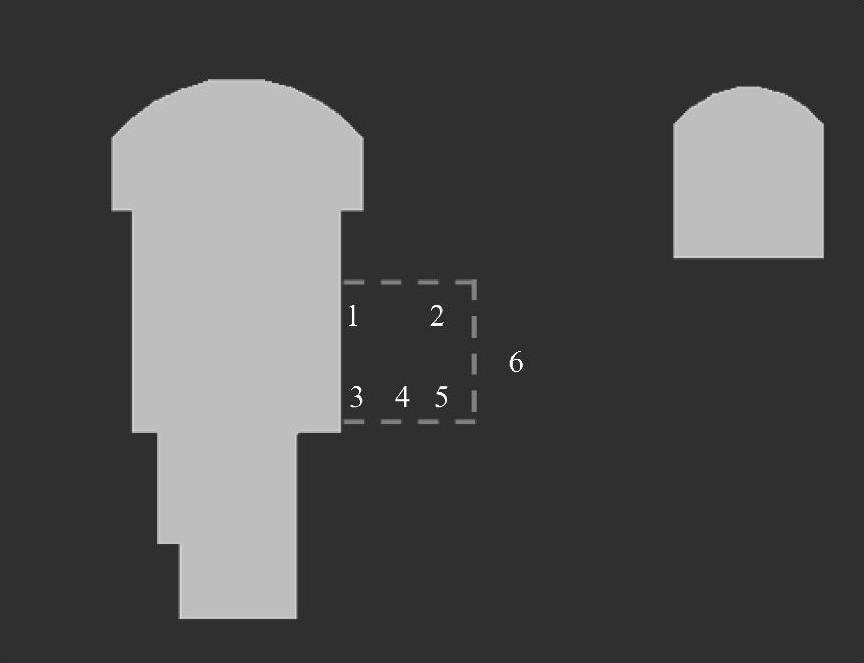
图6-9 关键单元布置图

1号和3号单元是洞室边墙附近的单元。从图6-10和图6-12中可以清楚地看到，两个单元在洞室开挖过程中都出现了明显的能量突降现象。出现能量突降的原因是，由于开挖的影响，使得洞壁围岩处的径向应力释放，量值大幅减小，虽然其切向的应力有一定的增加，但由前述的能量计算式（6-3）可以得到该部位的围岩的弹性能在总体上还是会出现较大幅度的减小。两单元的能量突变量分别为6280J和5349J。另外值得注意的是，1号单元的能量突降出现在时步0.3E+03处，而3号出现在时步1.5E+03处。这是由于1号单元与3号单元处于不同的开挖步所引起的。1号单元位于第三开挖步附近。而3号单元位于第四步开挖附近，距离开挖步越近，势必受到的应力扰动越大，因此能量的突降有时步上的差距。另外，从图中还可以看到，单元在较大应力降之后能量虽然有部分回弹，但是基本趋于稳定。主要是因为这些单元受后续开挖步的扰动较小，其应力状态改变较小，说明该单元基本达到一个稳定状态。

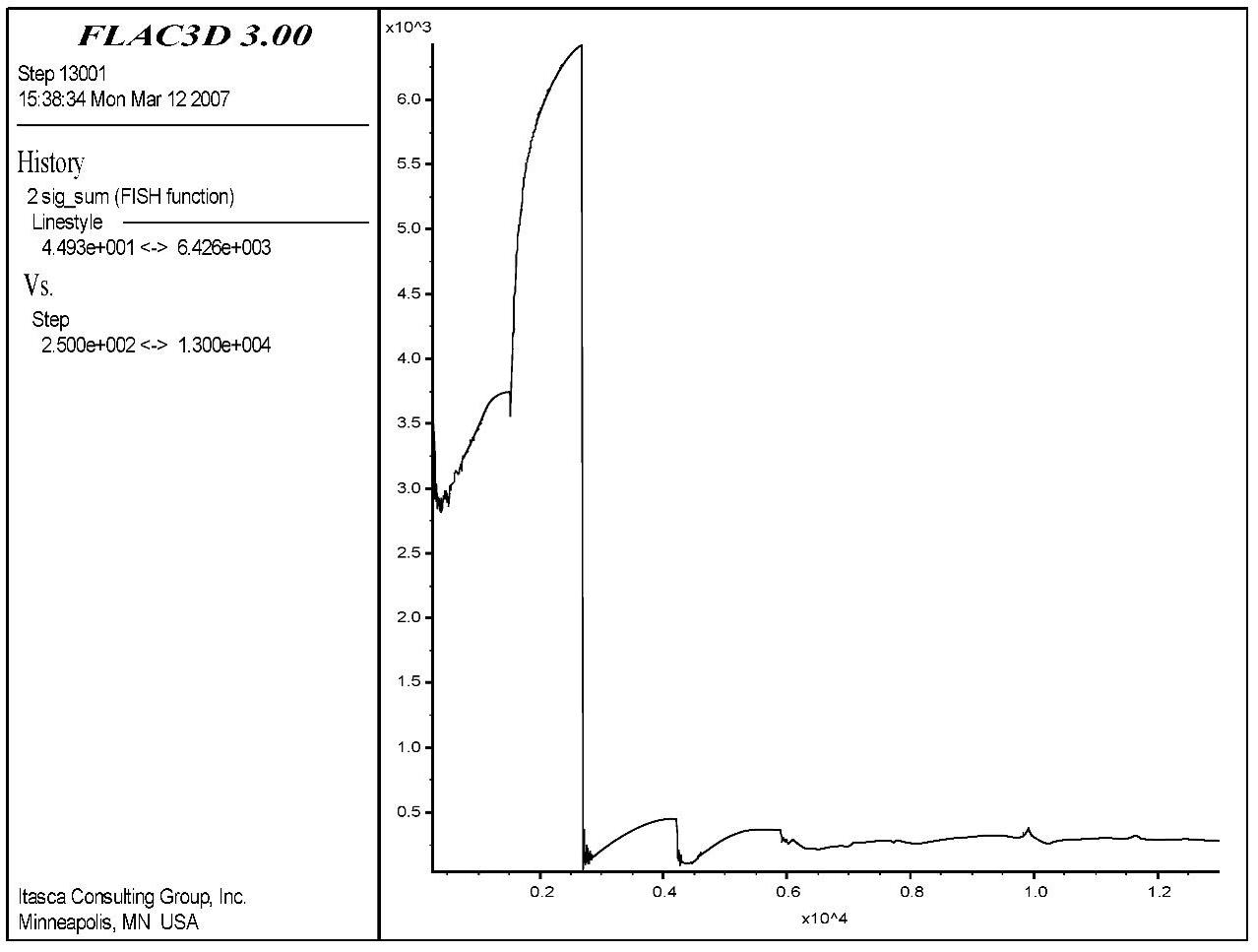
图6-101 号单元能量随时步变化曲线

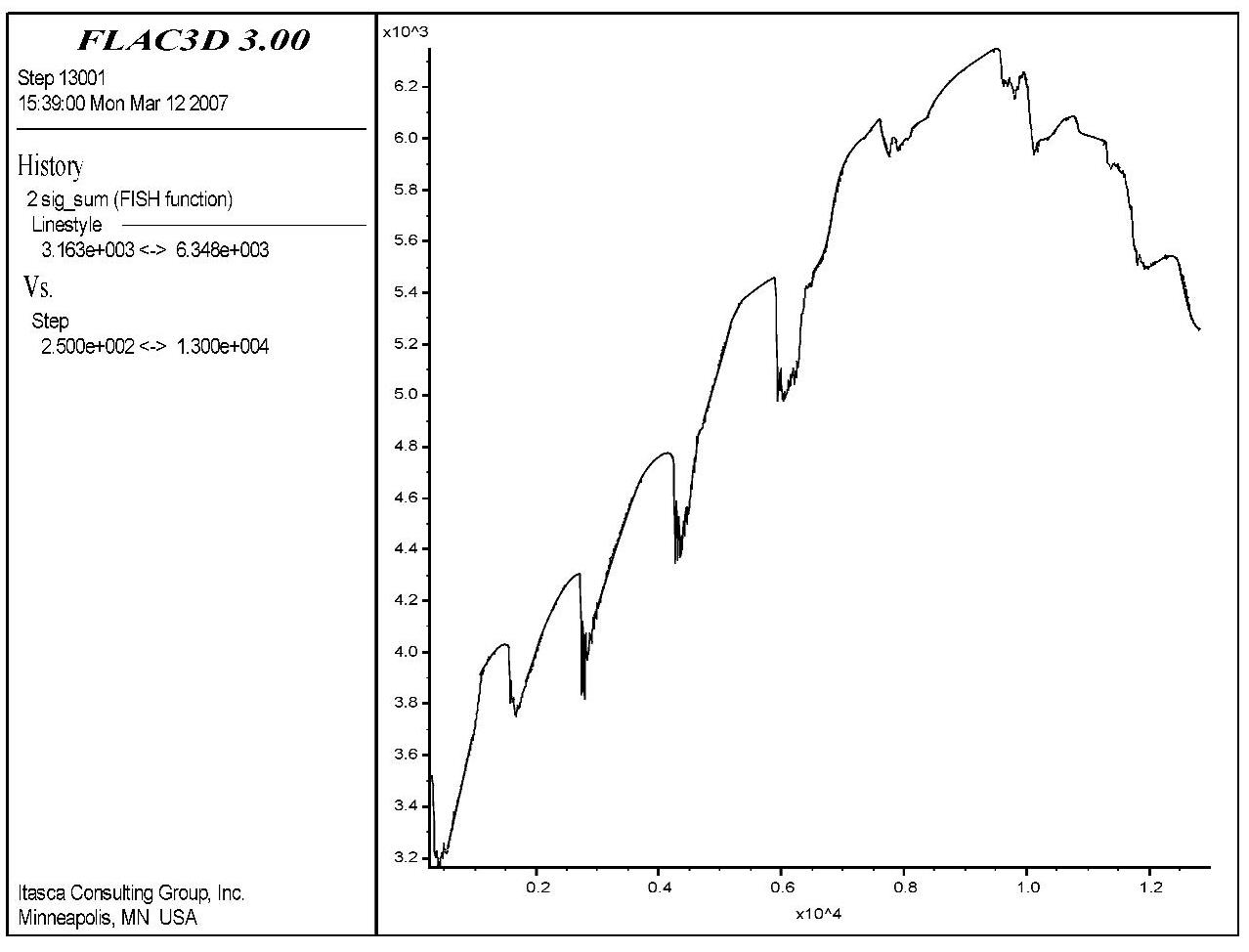
图6-112 号单元能量随时步变化曲线

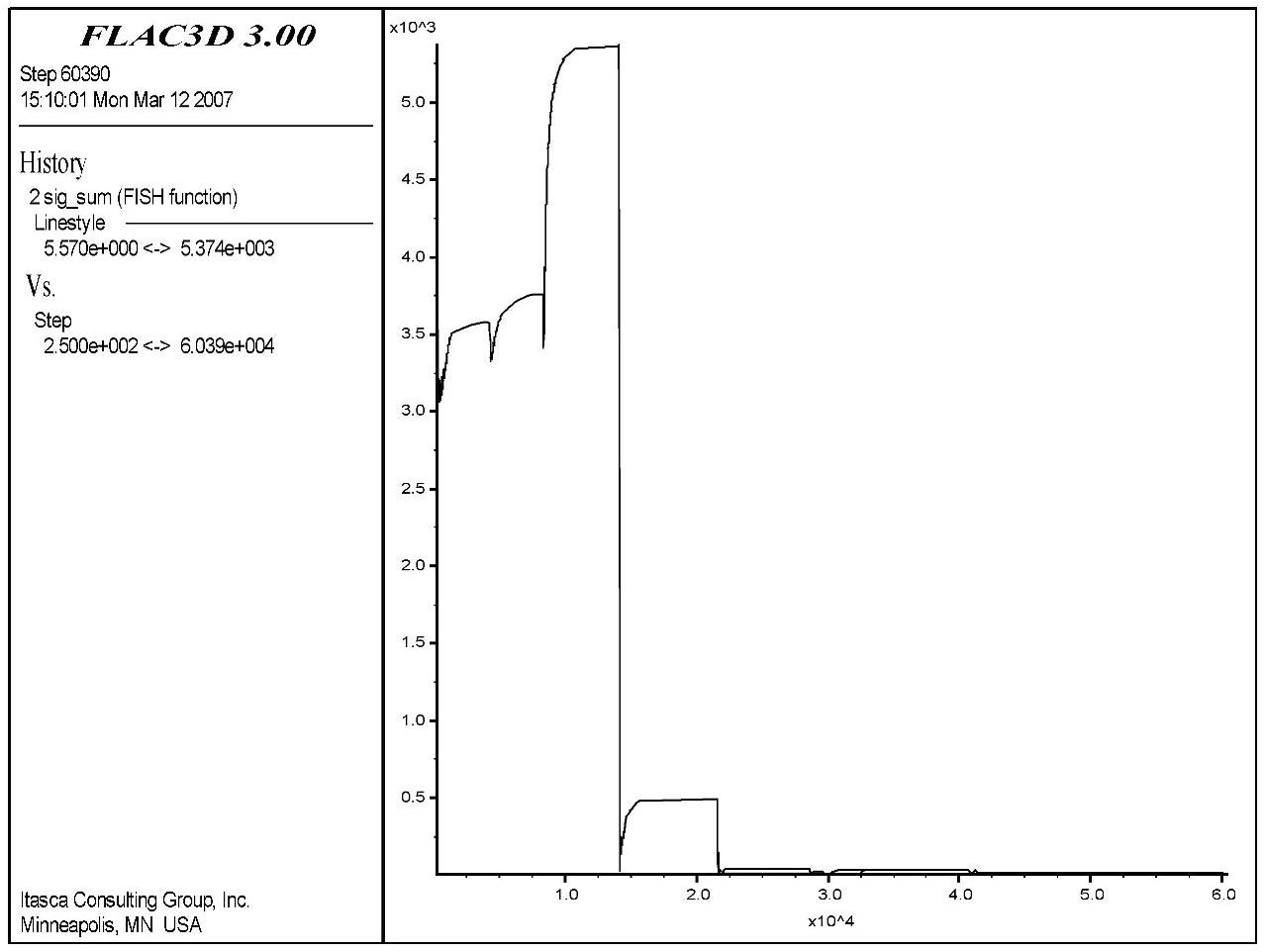
图6-123 号单元能量随时步变化

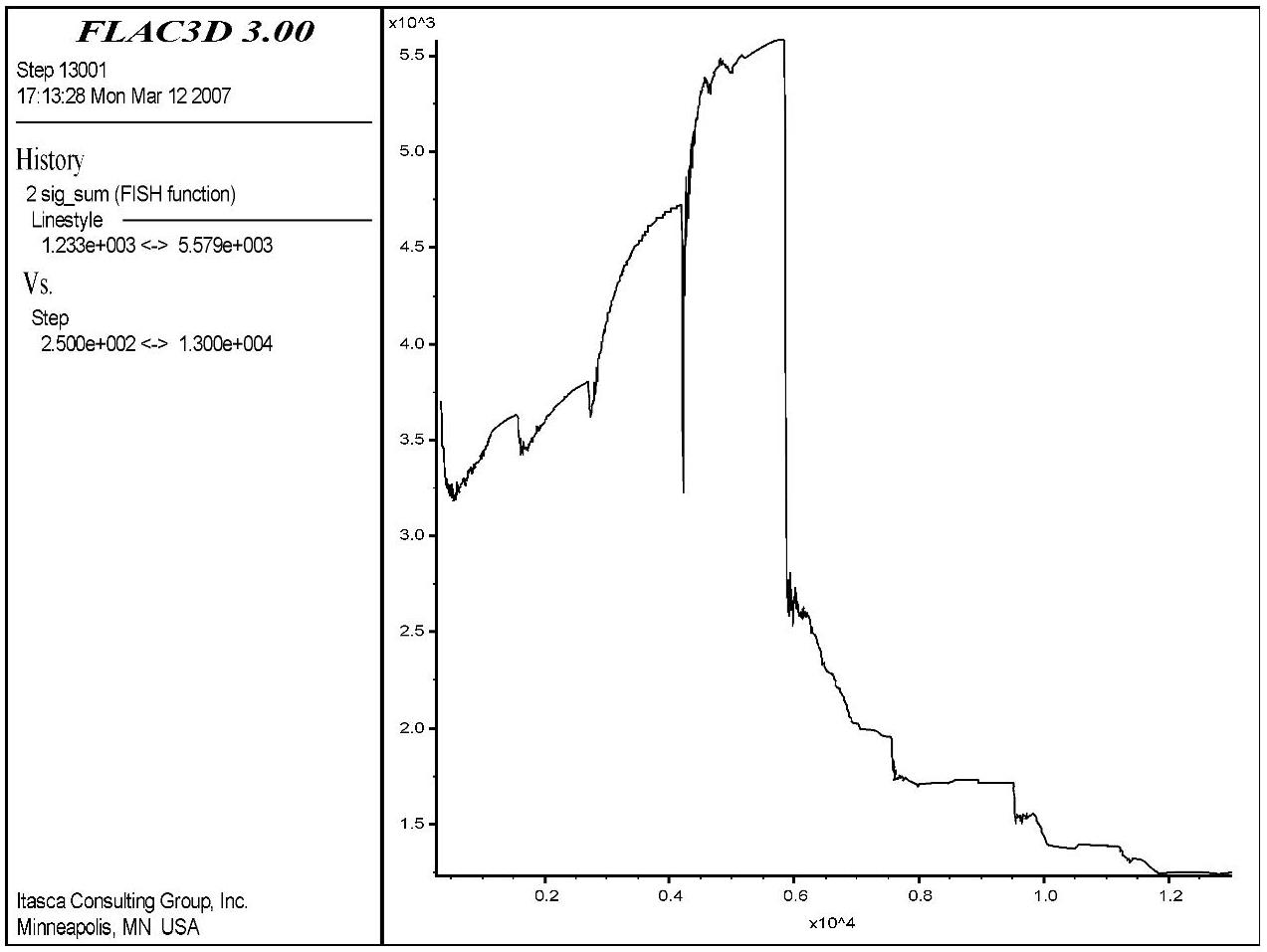
图6-134 号单元能量随时步变化曲线

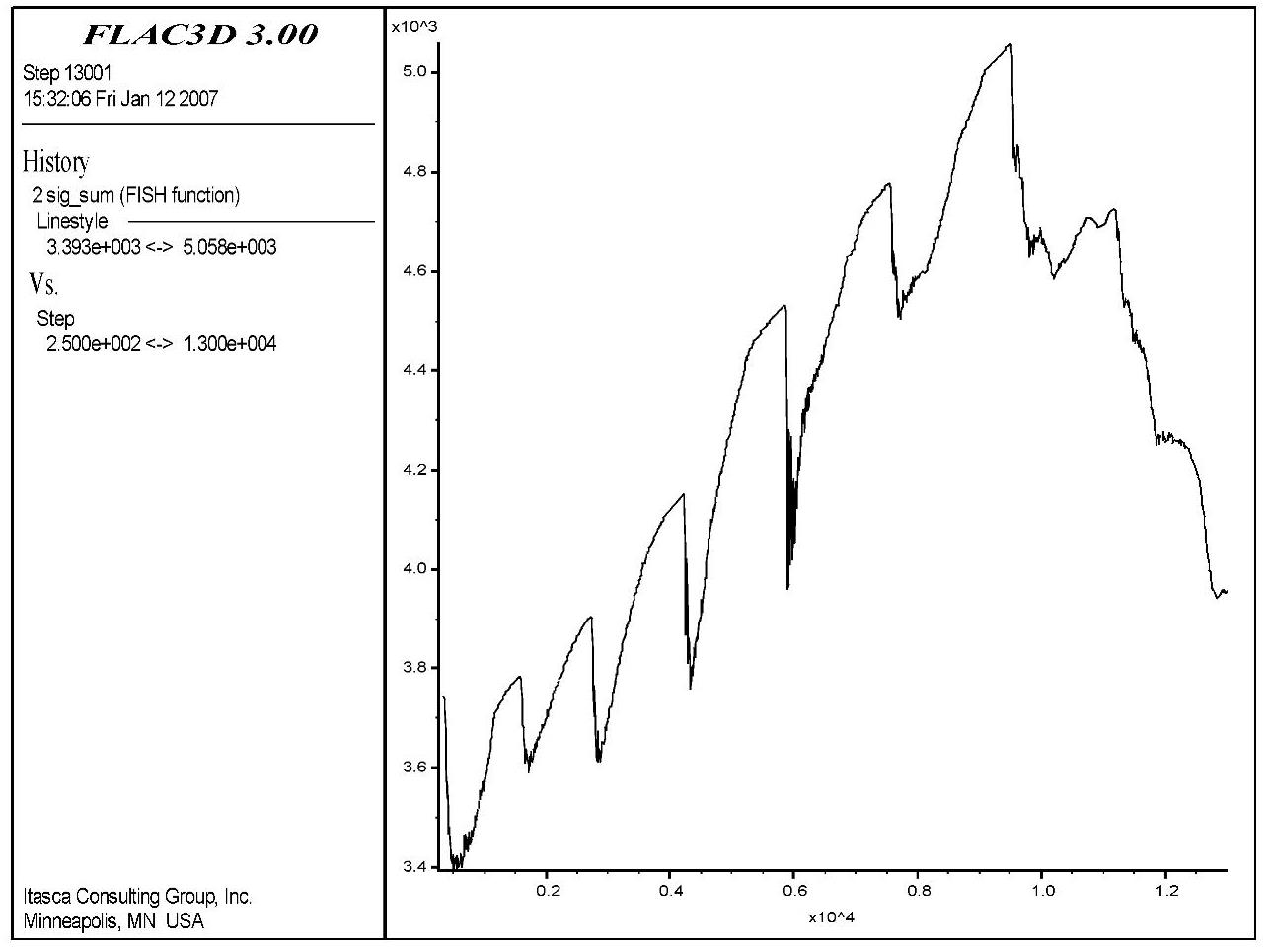
图6-145 号单元能量随时步变化曲线

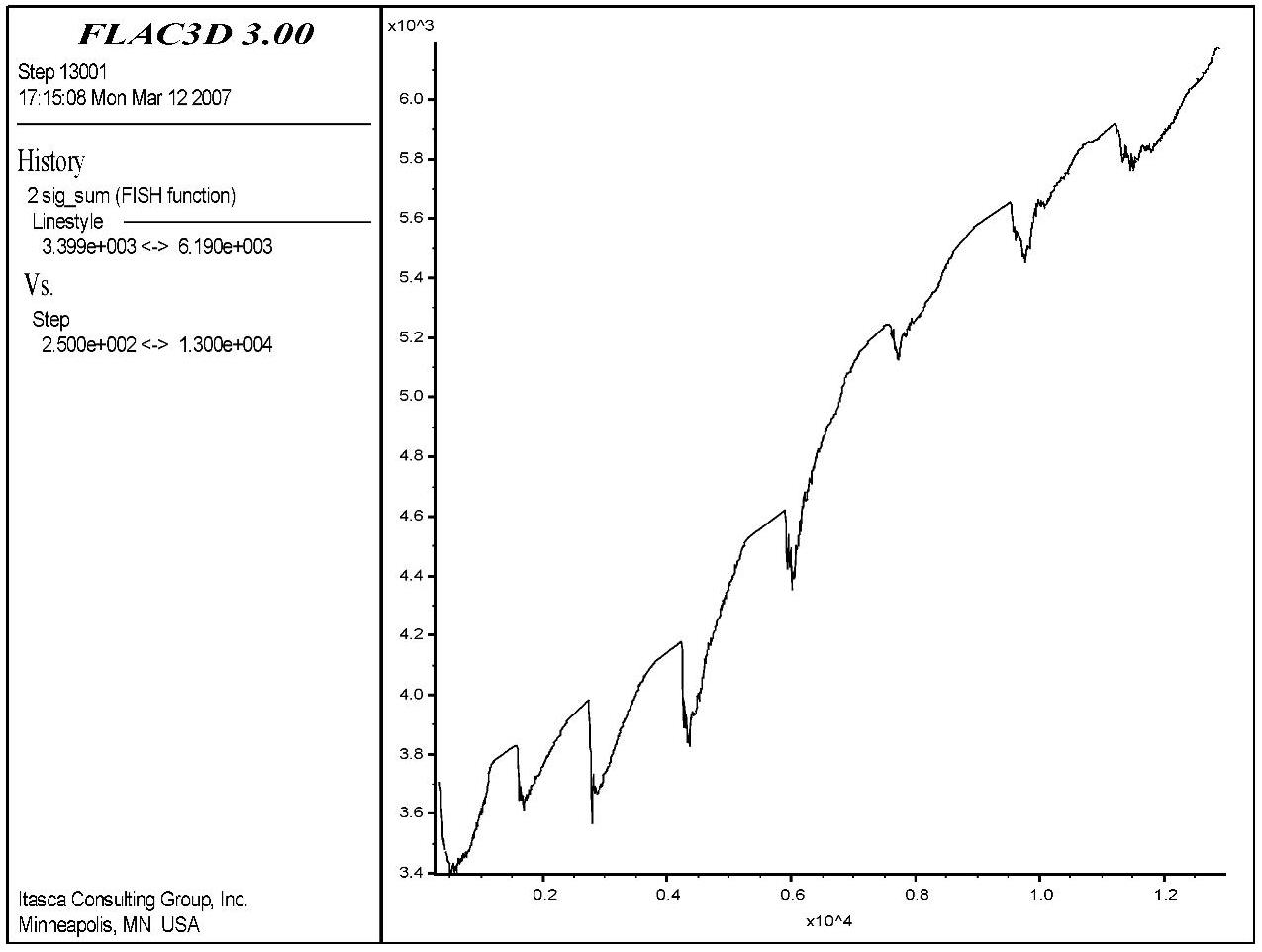
图6-156 号单元能量随时步变化曲线

4号单元是比1、3号单元稍远离主厂房洞室边墙的单元。通过图6-13可以看出此单元也受到洞室开挖的影响有较大的能量变化，其量值为3106J。但是相对1、3号来说，其变化量要小一些。说明开挖对洞室围岩的扰动随着向围岩深部变化而逐渐减小。

2号单元则比4号单元距离洞壁更远一些，它所受到的开挖扰动也相应地更小，能量变化值为600J左右。

比较1、3、4号单元的能量变化曲线与2、5号单元的能量变化曲线，我们发现：1、3、4号单元的能量在开始一段时间内都有一定数量的增长，即应力的变化引起其弹性能的增加，但最终的能量还是小于其初始能量的，即耗散掉了一部分能量用于塑性变形；2、5号单元的能量曲线在开始时逐渐上抬，经过能量突降之后，又逐渐下降，但最终的能量值大于其初始能量值，说明经过开挖之后该部位处的能量还是增加的。

6号单元是选取的区域以外一点，此单元在整个计算中处于弹性状态。从图中可以看出，其能量变化一直呈增长态势，每步开挖对该点影响不大，最大量值仅100J左右。

所选择区域开挖释放的总能量随着开挖步的变化趋势如图6-16所示。

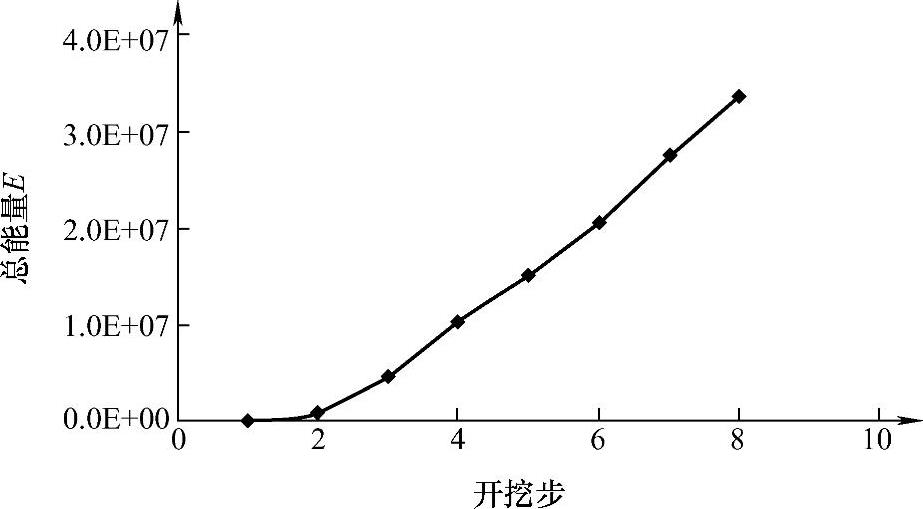
图6-16 主厂房围岩总能量耗散变化趋势

从图6-16中可以看出，释放的能量随着开挖的进行逐渐增加，大体接近线性增长趋势。当第八步开挖完成之后的耗散能达到了ΔU=3.36E+07J。结合第3章中提出的根据能量预测裂纹条数的公式，可以估算出所选区域里形成劈裂裂缝的条数n₀=ΔU/W_s，其中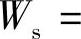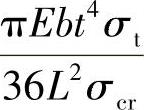，最后算得n₀=21条。与第四章的计算所得的条数基本接近，验证了使用能量分析方法预测劈裂裂缝的可靠性。