基于能量等式的地下洞室开挖岩体破坏分析

本章将基于本书提出的能量等式WD=SE+nW_s，用数值计算的方法来分析开挖地下洞室时，围岩局部集聚的应变能超过岩体的极限储存能而突然释放的能量。此能量假定全部用于劈裂裂缝形成的能量耗散。考察该能量的变化情况拟采用以下方法实现：在数值模拟计算中，采用适合脆性岩石的应变软化模型，通过追踪每个单元弹性能量密度变化的全过程，记录下单元发生破坏前后的能量差值，即为U_i=WD_i-SE_i。然后将所有产生塑性区的单元的能量值累加求得总和即为当前开挖步引起的围岩的总释放能量nW_s。

为了便于利用数值计算的数据结果，我们定义每个单元的能量计算表达式如下：

1）第i个单元破坏之前的弹性应变能，即

SE_i=V_i[（σ²₁+σ²₂+σ²₃）-2ν（σ₁σ₂+σ₁σ₃+σ₃σ₂）]/（2E） （6-1）

2）第i个单元的发生破坏时的弹性应变能量，即

式中 σ₁，σ₂，σ₃——单元破坏之前的主应力值；(www.xing528.com)

σ₁^∗，σ₂^∗，σ₃^∗——单元发生破坏时的主应力值；

ν，E——岩石单元未发生破坏时的泊松比和变形模量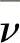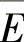；，——单元发生破坏后的泊松比和变形模量。

简便起见，假设破坏前后的泊松比和弹性模量不发生变化。则产生破坏区域内的能量变化可以表示为

以上所述思路通过跟踪每个单元破坏前后的能量变化，进而反映整个破坏区域的围岩在此过程中的能量耗散情况，以此来考察能量方法对于岩体破坏分析的适用性。