【摘要】：经过试算，微裂纹起始角度对判据影响较小，因此均取θ=45°，摩擦系数μ=0.5，，出现劈裂裂缝的长度别取四个不同量级长度进行分析，即：L=1m，5m，10m，20m。2）裂纹达到临界扩展点时，裂纹间距足够大没有导致微裂纹的连接，即l＜w。代入式（4-7），得由于脆性岩石微裂纹的分布受到颗粒的粒径尺度的影响，因此粒径的大小将对判据起到决定性作用。3）可以根据式（5-2）的判据来获得地下洞室围岩产生劈裂破坏的范围。
1）本书采用简化直线型裂纹组获得的产生劈裂裂缝简化模型获得的应力不等式作为产生劈裂破坏的判据，即
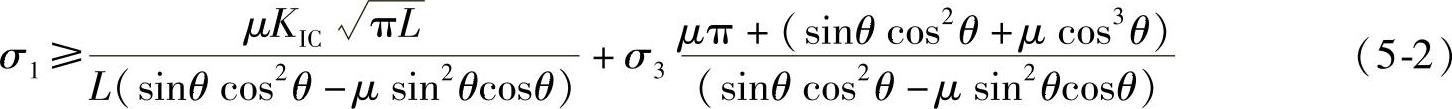
式中 μ——裂纹表面的摩擦系数；
L——形成劈裂裂缝的长度；
θ——初始裂纹与最大主应力的夹角。
此判据能描述应力与劈裂裂缝长度及其脆性岩石材料的断裂强度等特性。
以下将本书所研究的二滩工程的正长岩的相关参数代入式（5-2），可以得到定量的主应力之间关系表达式。
经过试算，微裂纹起始角度对判据影响较小，因此均取θ=45°，摩擦系数μ=0.5，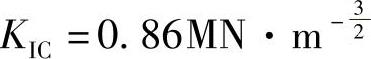
，出现劈裂裂缝的长度别取四个不同量级长度进行分析，即：L=1m，5m，10m，20m。代入式（5-2）可以获得不同的判据，见表5-1。
表5-1 不同裂纹长度的劈裂破坏判据表达(www.xing528.com)
针对以上判据的实际应用，将在第6章的数值分析方法中加以详细描述。
2）裂纹达到临界扩展点时，裂纹间距足够大没有导致微裂纹的连接，即l＜w。利用式（4-5）定性的分析此状态下的破坏判据。
若考虑裂纹间距是翼形裂纹长度的两倍，即w=2l0，初始微裂纹起始角度均取θ=45°，摩擦系数μ=0.5。代入式（4-7），得
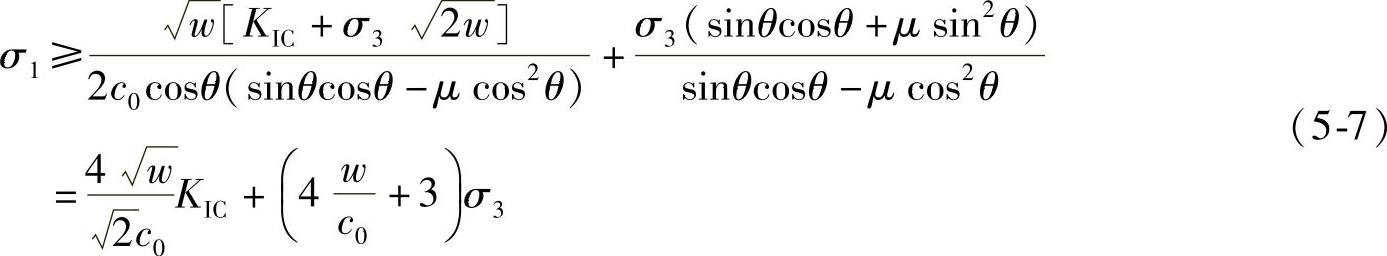
由于脆性岩石微裂纹的分布受到颗粒的粒径尺度的影响，因此粒径的大小将对判据起到决定性作用。
3）可以根据式（5-2）的判据来获得地下洞室围岩产生劈裂破坏的范围。然后利用本书提出的能量耗散模型来获得劈裂破坏区域所能产生的劈裂裂缝的条数，进而来预测围岩中所能引起的总位移。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
