薄板压屈能量耗散分析

第3章我们利用岩石试件中多条互不影响的平行裂纹扩展引起的能量变化来推求裂纹扩展的条数及其临界应变值。如果继续将此公式应用到实际工程中，可能适用性不强。因为工程中常出现的是比裂纹尺度大的劈裂裂缝，因此利用4.2节中的薄板压屈理论来分析工程中的劈裂裂缝的能量变化更切合实际。

为了定性的描述洞室附近的劈裂破坏，忽略开挖造成的应力分布不均匀现象。假定在区域为A×L×b的范围内已经形成n条等长度L纵向劈裂的裂缝。其裂缝的间距为t，如下图4-7所示。

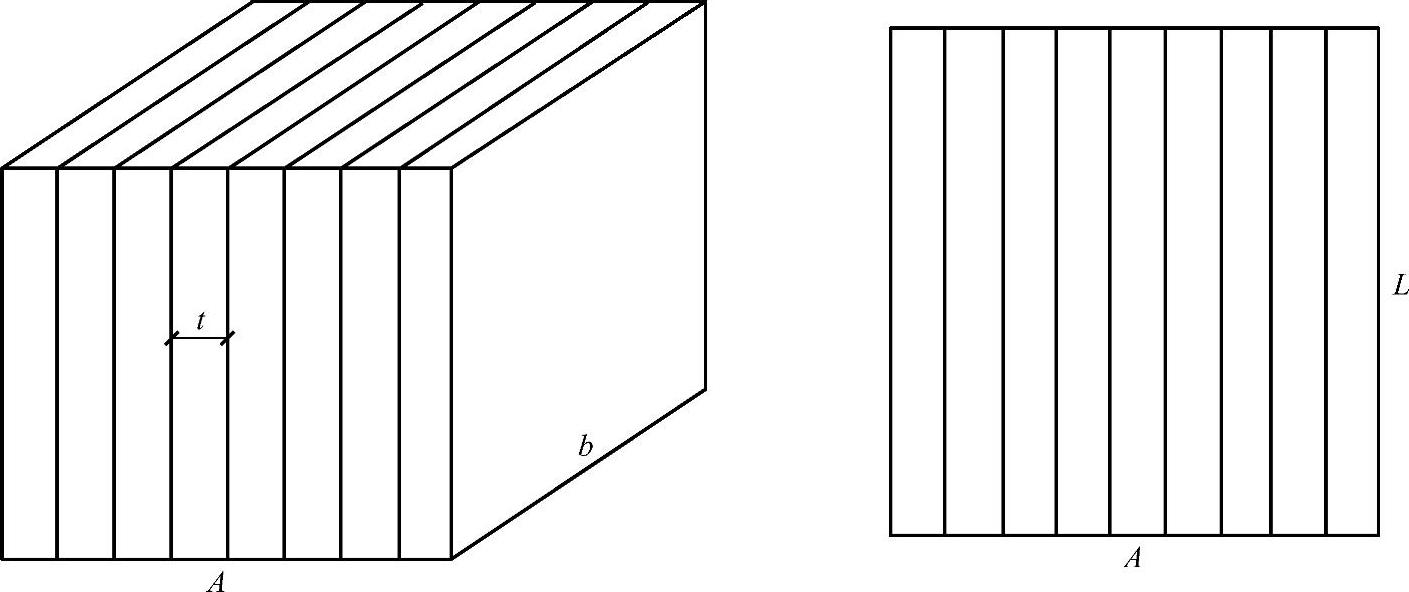
图4-7 岩柱中劈裂裂缝分布示意图

1.能量表达Ⅰ

根据能量等式WD=SE+nW_s可得

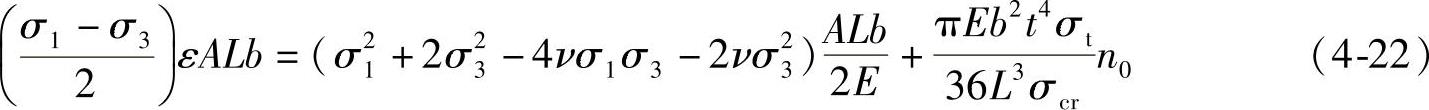
此能量等式与式（3-20）不同之处在于W_s的表达。根据式（4-22），就可以求得裂缝的条数。式（4-22）中条数n跟开裂深度A的关系有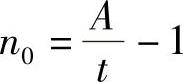或者。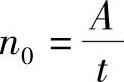

为了验证公式的正确性，采用二滩工程地下厂房的地应力参数与岩体力学参数进行验算。由于开挖后σ₁≫σ₃，简便起见，忽略侧向压力σ₃的影响。σ₁取产生劈裂破坏时的临界值σ′_cr，对于二滩工程地下厂房，A≈20m，σ′_cr=0.2σ_f=30MPa，ε_cr=2×10^-3，劈裂裂缝的长度L=5m，裂纹之间的宽度为t=0.5m，纵向深度b=20m；岩石的抗拉强度σ_t=5MPa，变形模量取E=30GPa。

能量公式（4-22）简化为

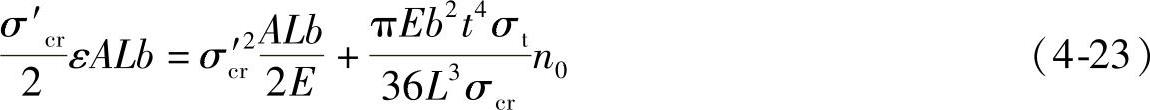
式中 σ_cr——单条劈裂裂缝的极限强度值式（4-20），将其表达式代入式（4-23），进一步整理可得

令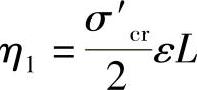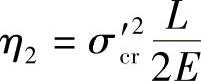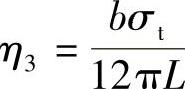；；为常数，则有以下关系式，是关于A和n及t的表达式

（η₁-η₂）A=η₃t²n₀ （4-25）

如果公式中的裂缝开裂深度和裂缝之间的平均宽度可以通过实测获得，那么岩石中的裂纹条数就可估算出来。若裂缝条数可以按照此计算公式n₀=A/t算的话，裂缝的宽度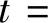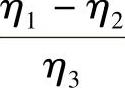，根据实际数据代入得到t=0.72m，这个数值应该是t的最小宽度值，对应裂缝的条数是28条左右。

2.能量表达Ⅱ

以下对WD=SE+nW_s采用不同的能量表达方式来进一步验证方法Ⅰ的可行性。

假如选取的分离体纵向长度比岩柱的宽度大很多，满足薄板要求，那么能量等式中的弹性能就可以用薄板原理等效获得。

（1）所取岩柱的弹性应变能SE可以按照以下方式进行计算。

1）柱的边界条件为ω（0）=0，ω（l）=0，ω′（0）=0；ω′（l）=0(www.xing528.com)

柱的挠度方程可以表示为

式中 u——柱中间挠度。

2）根据弹性力学理论知识可以获得，岩柱中的弹性应变能为

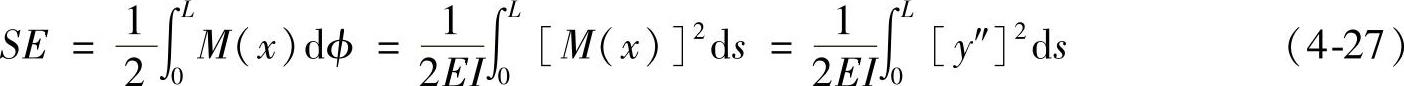
式中 E——变形模量（MPa）；

I——惯性矩（m⁴）；

M（x）——弯矩（N·m）；

ds——微弧长，其表达式为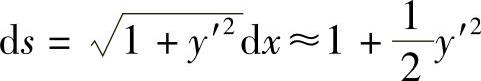

最后整理得到弹性应变能的近似解为

式中 u_e——可以通过计算获得为。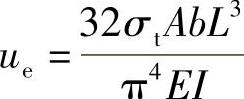

（2）岩柱中的总能量WD

依然可以采用外力做功大小来表示为WD=σ_cruAb，式子中u为实际岩柱中产生的变形量。

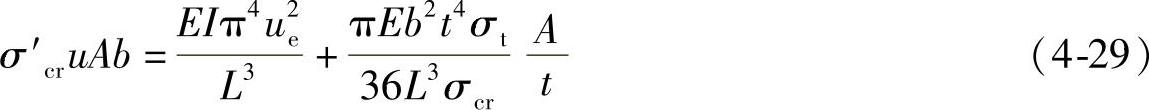
将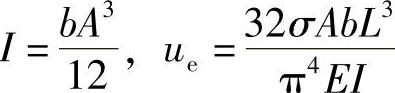带入式（4-29）得到简化的能量公式如下

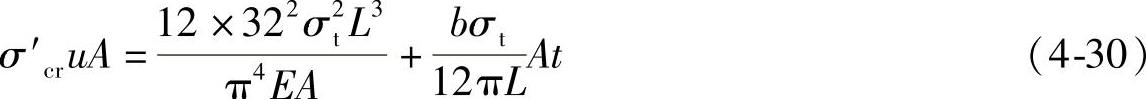
式（4-30）中已知量为σ、u、E、L，因此上面的公式就是A和t的函数。令σ_cru=Δ₁，，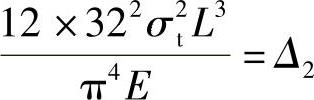

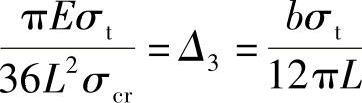
若已知A=20m，则推求出t=0.85m，条数n₀=24条。