【摘要】：它的挠度方程简化为式中 m，n——薄板压屈以后沿x和y方向的正弦半波数。纵向荷载N的临界值一定满足如下的压屈条件，即整理得压曲的临界荷载应该取n=1，即让薄板沿着y方向只有一个正弦半波。于是临界荷载就是式中 。薄板的边界条件为。通过计算得到薄板压屈的临界应力值有了薄板破坏时的强度值之后，当薄板达到临界应力状态时释放的能量值为。
由于洞室边墙处劈裂裂缝等效为薄板压曲，因此其力学模型可简化为两承载边为简支约束，另两边自由（见图4-6）。
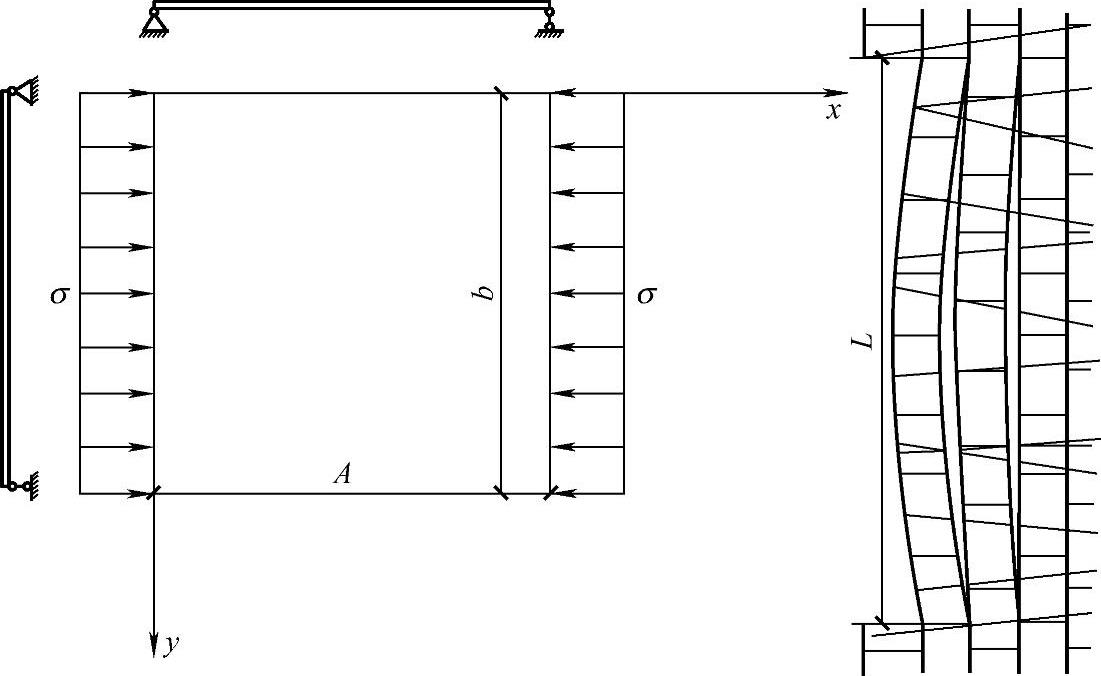
图4-6 薄板压屈示意图
于是有Nx=-N，Ny=0，Nxy=0，将已知力代入式（4-10）得到
取挠度表达式为
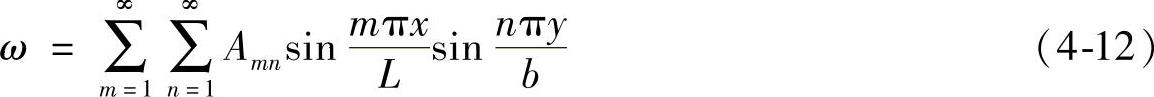
将挠度方程代入简化后的微分方程得到
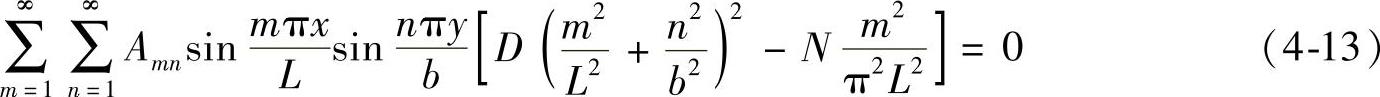
由式（4-13）可以看出，如果荷载N很小，则无论怎样，方括号里面的数值总是大于0，因此系数Amn都必须大于0。但当N增大，使得方括号里面的数值变为0，因此系数Amn可以不为0而又满足微分方程，此时薄板可能压曲。它的挠度方程（4-12）简化为
式中 m，n——薄板压屈以后沿x和y方向的正弦半波数。
纵向荷载N的临界值一定满足如下的压屈条件，即
整理得
压曲的临界荷载应该取n=1，即让薄板沿着y方向只有一个正弦半波。于是临界荷载就是
(https://www.xing528.com)
式中 
。
有了临界荷载，那么临界应力的通式为
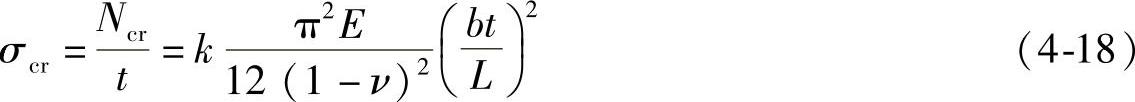
式中 L——劈裂裂纹的长度；
t——薄板的宽度。
另外引用缪协兴等[155]，简化模型的挠度方程可以写为
式中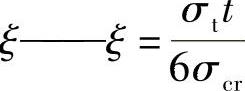 
；
σt——岩石的抗拉强度。
薄板的边界条件为
。
通过计算得到薄板压屈的临界应力值
有了薄板破坏时的强度值之后，当薄板达到临界应力状态时释放的能量值为
。
通过整理获得形成薄板后弯曲所产生的能量
此能量表达式与围岩的抗拉强度和薄板的抗压强度有关系，可很好地反映围岩内部形成这种薄板式的劈裂裂纹的能量变化。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
