翼形裂纹临界长度与临界间距的确定方法

本节的目的是确定微裂纹扩展的临界长度及其应力状态，以及形成劈裂裂缝需要的裂纹之间的最小距离等。

图4-3所示为滑移型裂纹模型示意图，这种裂纹模型最早用来研究岩石的剪胀现象。裂纹体由初始裂纹以及翼形裂纹组成，其中翼形裂纹是由于初始裂纹面在远场压应力作用下相对滑移引起的。

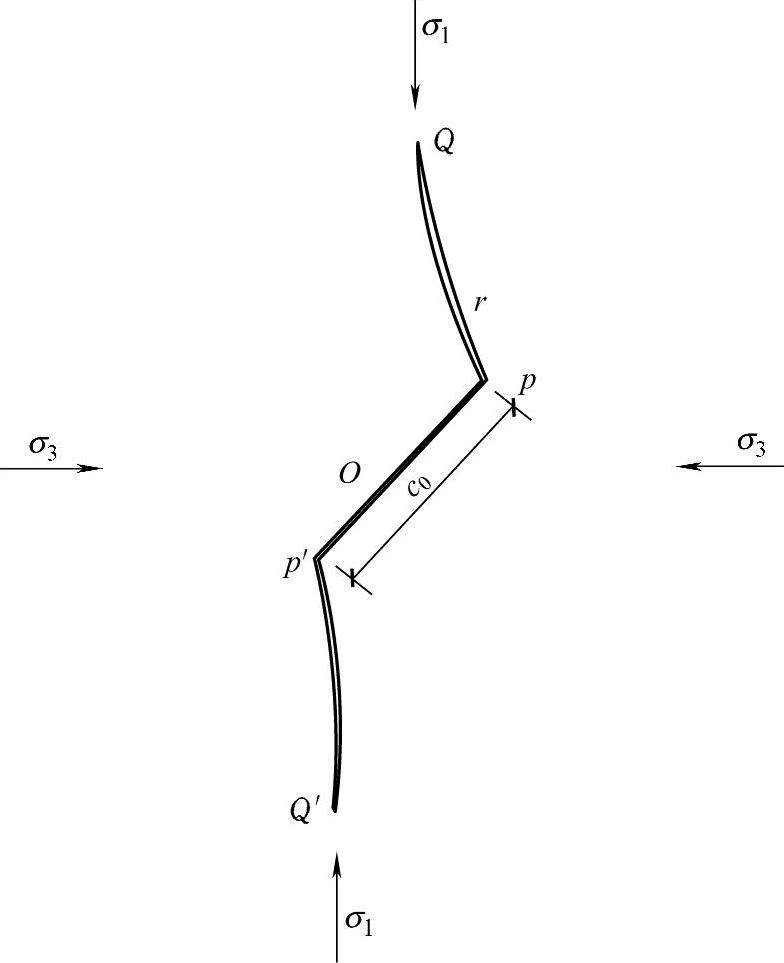
图4-3 滑移型裂纹模型示意图

许多学者通过试验以及理论分析指出，翼形裂纹最初沿与初始裂纹成70°方向发展，并很快与最大压应力方向平行。基于这些研究，在此我们将上图中的翼形裂纹简化为直线型滑移裂纹，如图4-4a所示。

图4-4中，直线型的拉伸裂纹沿平行于最大压应力的方向扩展。同时，采用图4-4b所示的一组滑移型裂纹模拟岩石在压应力作用下的劈裂破坏模式以及考虑裂纹之间的相互作用。图4-4中，初始裂纹长度为c₀，翼裂纹长度为l₀，相邻裂纹间距为w，初始裂纹面与水平方向之间夹角为θ。滑移面摩擦系数为μ，相邻两裂纹间隔距为w。当l₀=w时，裂纹发生连接。

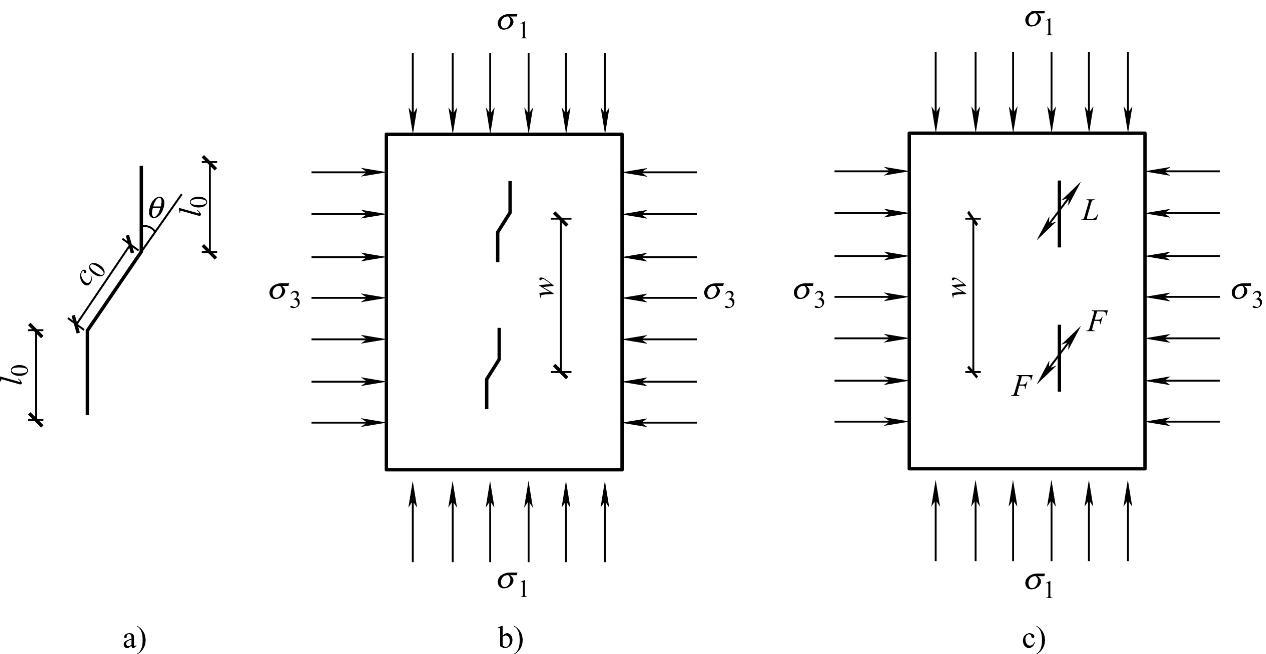
图4-4 直线型滑移型裂纹示意图

进一步简化裂纹模型如图4-4c和图4-5所示，即一组拉伸裂纹承受集中力F以及远场压应力的作用。力F反映了作用在初始裂纹面上的剪切力对拉伸裂纹的作用，因此忽视初始裂纹面上的斜截面上剪切应力的影响。

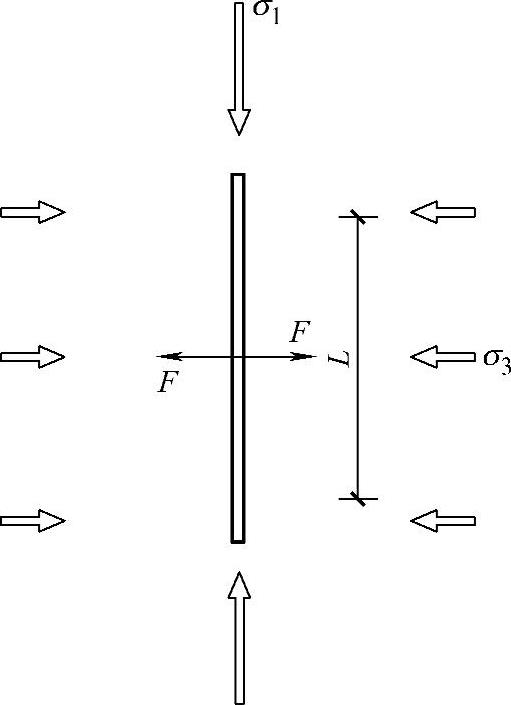
图4-5 宏观劈裂裂缝示意图

τ^∗为一条裂纹（见图4-4a）滑移面上由于σ₁和σ₃作用下产生的有效剪切应力，可以表达为

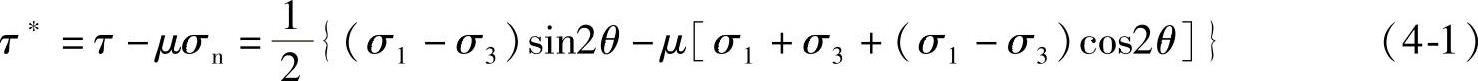
式中 τ——裂纹面的切向应力；

σ_n——裂纹面的法向应力。

对单个裂纹，翼形裂纹所受的张力f可以设为有效剪应力在水平方向的投影，即

f=τ^∗cosθ （4-2）

扩展到整个裂纹面上的张力合力F可以等效为

式中 A——劈裂裂纹表面面积。

将式（4-1）和（4-2）带入式（4-3）得

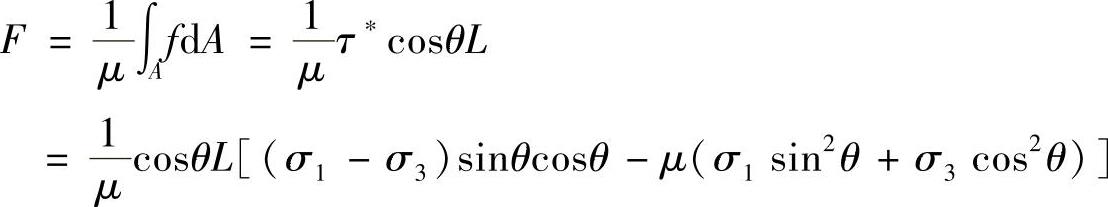
裂纹的繁衍受到裂纹尖端应力强度因子K_I的影响。那么形成劈裂裂缝的K_I（见图4-5）可以表达为

由于不考虑裂纹的摩擦，II型裂纹引起的应力集中可以忽略不计，因此可以利用K_I≥K_IC可以获得应力之间的σ₁和σ₃之间的不等式，即

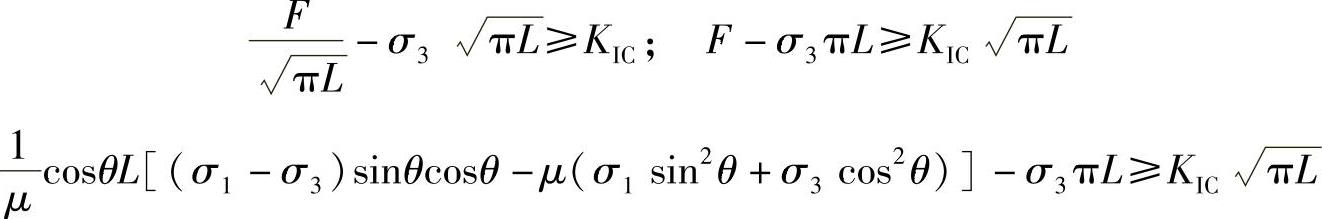(www.xing528.com)

最后整理得到，产生劈裂破坏后的应力不等式如下

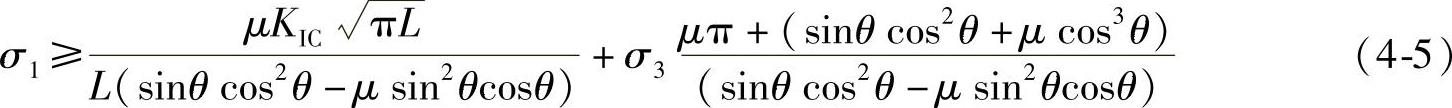
依据比不等式可以作为围岩产生劈裂破坏的判据。

式中 μ——裂纹的摩擦系数；

L——形成劈裂裂缝的长度；

θ——初始裂纹与最大主应力的夹角。

通过式（4-5）可以看出，此判据同样是跟裂缝的能量和长度相关，与第3章微观分析得到的应力表达公式类似，不同的是此公式是从宏观尺度上表征形成劈裂裂缝的判断方法。

下面分析裂纹扩展后未产生劈裂贯通时的应力间的关系，即l₀＜w。图4-4c所示的裂纹的裂纹尖端应力强度因子K_I^[153]可表示为

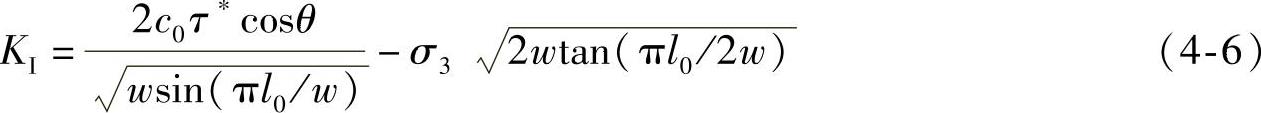
式中 σ₃——最小主应力。

同样利用K_I≥K_IC产生破坏这一临界条件可以获得

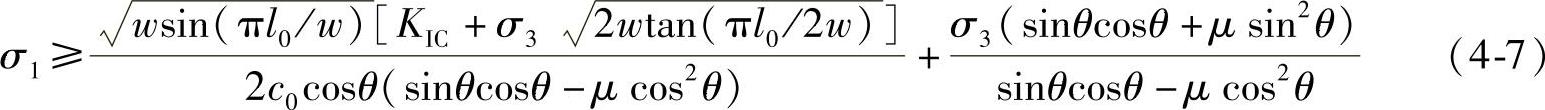
式中 l₀——翼形裂纹长度；

c₀——初始裂纹长度；

w——裂纹间距。

式（4-7）仅适用于每条裂纹独立扩展，未实现裂纹间贯通时的应力不等式。

讨论：

1）当σ₃较大时，由于σ₃的存在，K_I降低，这将抑制裂纹的扩展。主要表现为：①减少裂纹张开度；②减小裂纹表面的张力F（等效到未简化裂纹就是降低裂纹表面的剪应力）。但是，当裂纹扩展的长度l/l₀≫1的时候，即裂纹扩展长度比原裂纹长很多时候，侧向压应力σ₃对裂纹表面的张力F的影响可以忽略不计。

2）假设地下洞室开挖后，洞室围岩附近σ₃较小，此时式（4-5）中σ₃可以忽略不计，即σ₃=0。

上述两种情况下，可以推求出

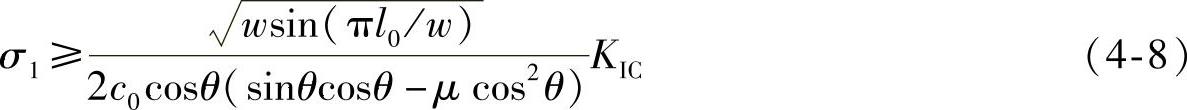
由式 （4-6）推导出致使翼形裂纹相互连接的临界扩展长度为

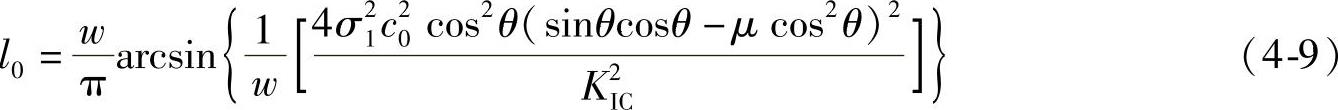
因此当l₀=w时，式（4-9）达到临界状态，使得裂纹产生连接形成劈裂裂缝。更详细的讨论分析将于第5章节详述。