脆性岩石黏结弱化与摩擦强化效应分析

根据裂纹所吸收的能量达到裂纹的表面能时，裂纹即开始扩展这一临界状态，即W_s≥4γ。将式（3-4）和式（3-17）代入W_s≥4γ，可以得到

通过式（3-32），可以推导出σ₁和σ₃的关系式。将τ和σ_n代入式（3-32）得到

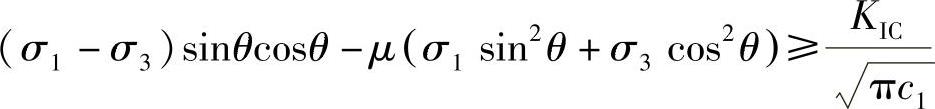
将上式两边同除以sinθcosθ得到

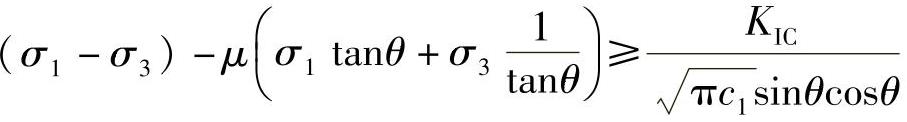
整理得

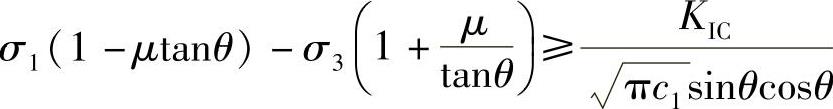
最后得到

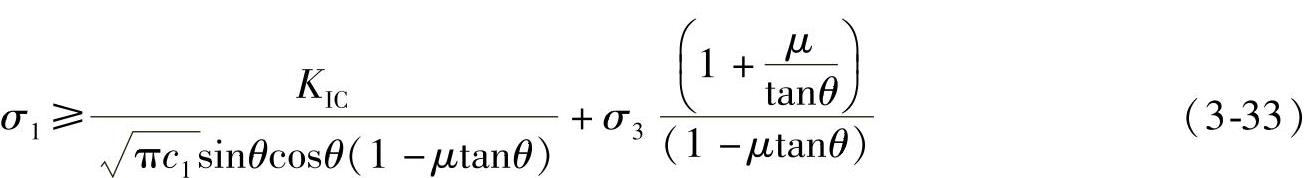
值得注意的是当θ达到θ_cr临界值时，将与摩擦系数相关，即使得不等式（3-33）右侧达到最小值。

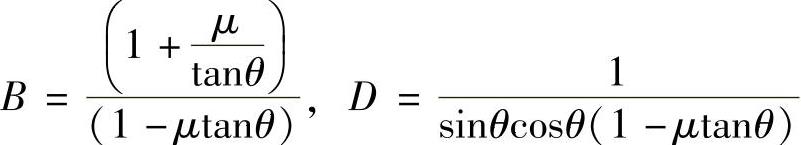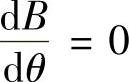令，因此当和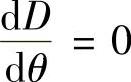时，将使不等式（3-33）右侧达到最小值，由此得到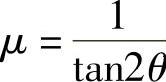，这就得到摩擦系数和裂纹角度的定量表达关系式。

利用μ和θ的关系将不等式中的θ消掉，得到新的公式如下

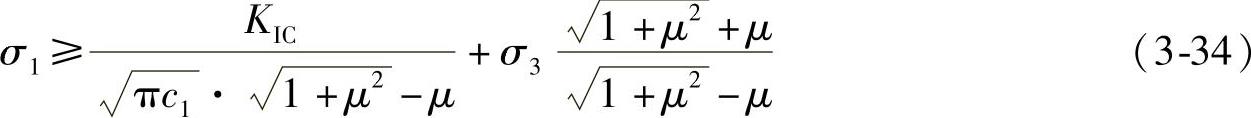
由于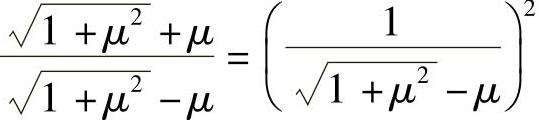，因此式（3-34）可变换为

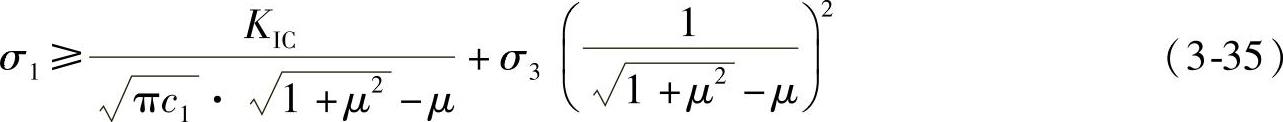
又由于μ=tanφ，φ是岩石材料的内摩擦角，得

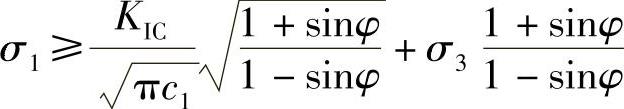
又因为

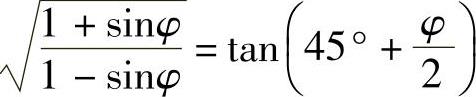
所以式（3-33）最后整理得到

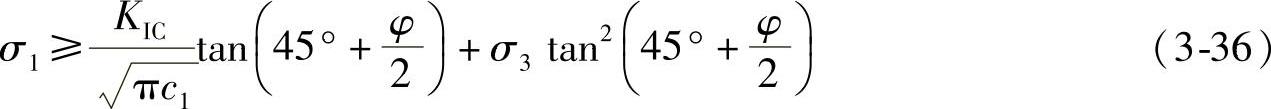(www.xing528.com)

式中 K_IC——裂纹的断裂强度因子；

c₁——裂纹的临界长度；

φ——岩石材料的内摩擦角。

因此不等式（3-36）与摩尔-库仑准则相近，但它是由考虑了裂纹达到临界扩展的能量准则推算出来的。其中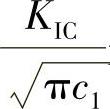是跟裂纹有关的元素，它与材料的黏聚力有关，令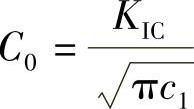，不等式（3-36）变为

在地下洞室开挖中，边墙附近的由于卸荷作用可使得σ₃≈0，因此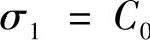。裂纹产生滑移扩展的临界应力值通过全应力应变曲线应该是非稳定扩展点，因此C₀=σ_cd。有了应力的临界值，计算裂纹条数的公式将容易解出。

值得注意的是，Martrin^[59]曾提出的在岩石试件中，随着应力水平提高，裂纹扩展不仅仅会引起黏聚力的降低同时也会引起内摩擦角的增大。他提出内摩擦角的公式为

其黏聚力和内摩擦角的变化图可以通过下面的无量纲图分析。首先通过全应力-应变曲线获得岩石试件的σ_f、σ_cd以及总的体积应变ΔV₀，然后对岩石试件进行卸载试验，每次卸载的应力值取σ_f与σ_cd之间相同的数值，观察σ_cd随加卸载的变化过程。其中，σ_cd可以通过体积应变曲线的转折点获得，内摩擦角φ可以通过式（3-38）获得。图3-7a的横坐标为第i次卸载的总体积应变与无卸载时总体积应变的比值，即ΔV_i/ΔV₀；纵坐标为每卸载一步所获得的σ_cdi与峰值强度的比值，即σ_cdi/σ_f。图3-7b的右侧纵坐标是每个卸载段的黏聚力与试件中岩石初始最大黏聚力的比值C_i/C₀，左侧为内摩擦角φ_i。

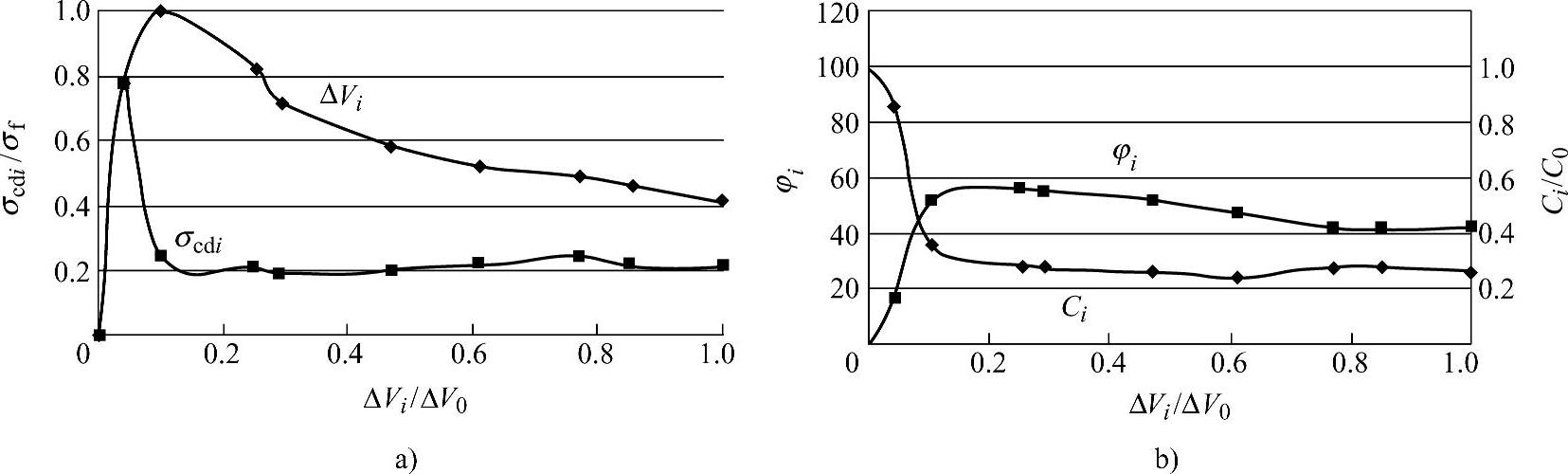
图3-7 内摩擦角和黏聚力随体积应变的变化曲线

图3-7与图3-8是选取二滩水电站实际工程一组标准试件所做的加卸载试验分析图。从图3-7b中可以看出，摩擦角的峰值是58°左右，此时黏聚力也有明显的跌落。随着裂纹扩展的继续进行，最终内摩擦角维持在41°左右。从图3-7a和图3-8中可以看出，随着加卸载的进行，σ_cdi经历了一个先增大后逐渐衰减的过程。说明此过程中，岩石的承载能力逐渐降低。多次加卸载后，在较低的应力水平下岩石就会发生失稳。

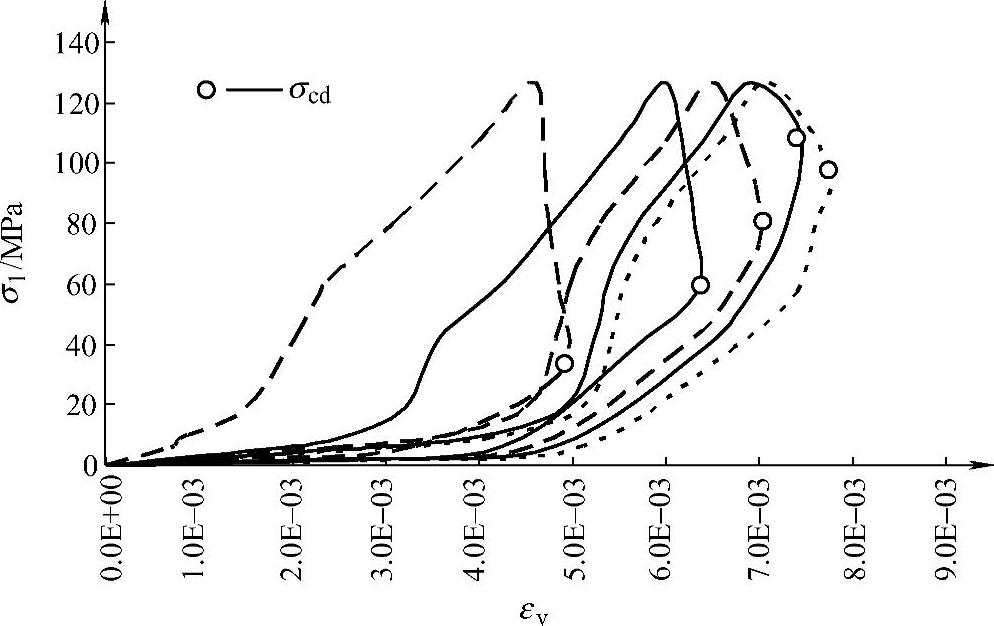
图3-8 σ_cdi随加卸载变化图

通过莫尔应力圆（见图3-9），也可以清楚地了解到黏聚力和内摩擦角的变化过程。同时，根据莫尔应力圆，可以得出裂纹的方向角与内摩擦角有如下关系

式（3-39）也验证了上文中获得的摩擦系数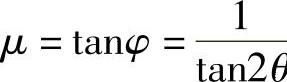θ的等价关系。

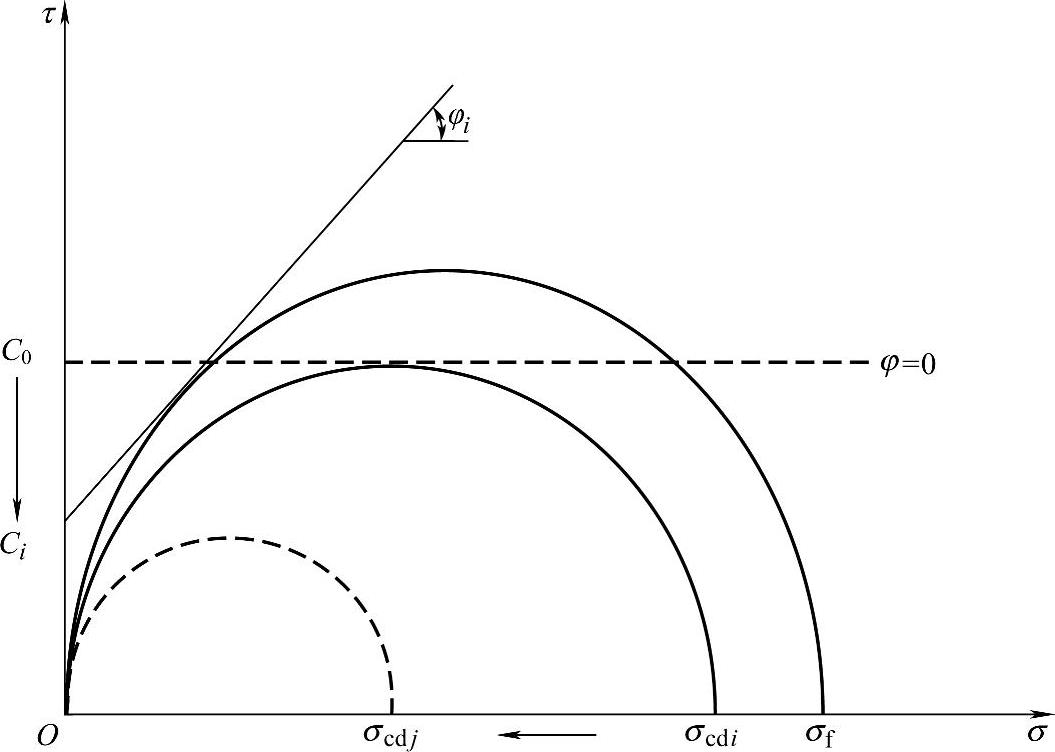
图3-9 黏聚力损失与内摩擦力增加的莫尔应力圆示意图

因此裂纹最终开裂后，与主应力方向的夹角随着应力水平提高引起的内摩擦角变化而改变。刚开始时刻，由于岩石试件不受荷载作用，无损伤发生，裂纹不扩展，那么此时内摩擦角φ=0°，则θ=45°。随着裂纹扩展，损伤开始出现，测得φ_max=58°（见图3-7b），因此求得最小的θ=16°，此时σ_cd也达到最小值。此处的θ是裂纹与最大主应力方向的夹角，此数据解释了岩石中容易出现近似纵向的劈裂裂纹的原因。