裂纹扩展能量分析在压缩荷载下的研究

本节将对滑移型裂纹在压缩应力下的裂纹扩展进行能量分析，受力状态如图3-4所示。

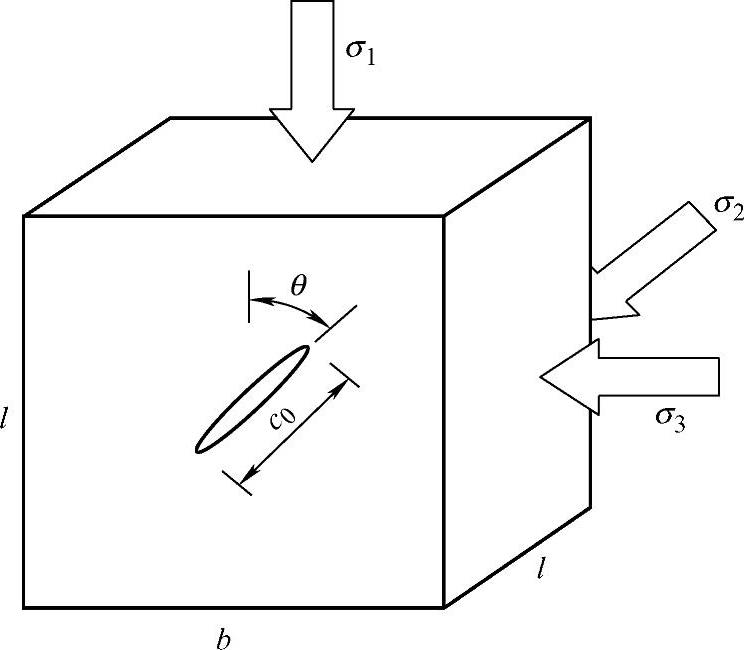
图3-4 三轴压缩状态下Griffith裂纹扩展条件

Starr^[148]给出了平面应变情况下裂纹表明的应变能为

式中 τ——裂纹表面的剪切应力。

式（3-12）没有考虑裂纹表面摩擦力的作用。如果考虑摩擦力作用则能量表达变为

式中 _μ——裂纹的摩擦系数；

σ_n——裂纹表面的法向压应力，假定裂纹相对于试件尺寸很小，根据一点的应力状态，则

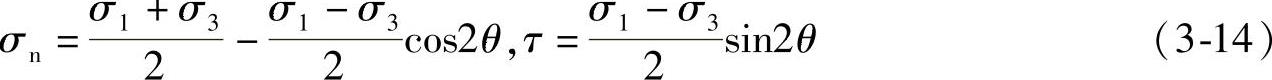
式中 θ——裂纹与最大主应力方向的夹角。

由于裂纹表面摩擦力的存在，如果裂纹产生滑移扩展必须使得裂纹的剪应力超过摩擦力才可能发生，即τ≥μσ_n。

因此，整个岩石试件中总能量WD包括：试件中的弹性应变能SE；裂纹扩展引起的能量耗散值W_s，即WD=SE+n·W_s，其中n是裂纹条数。

1）WD是由于外部应力引起的，其表达式是应力和试件整体应变的函数，即

2）试件的弹性应变能

首先无裂纹完整岩石试件中三个方向的弹性应变为

若考虑σ₂=σ₃因此弹性应变能就变为

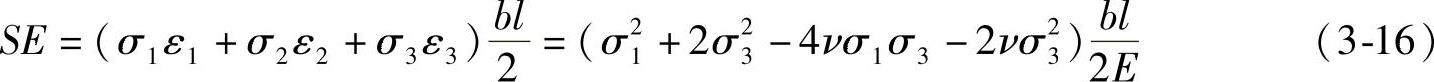(www.xing528.com)

3）裂纹扩展所需要的能量，即

利用上述各能量表达式获得下面等式

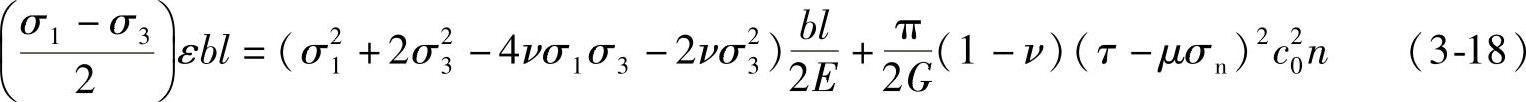
推得

令，代表单位体积的裂纹条数，则

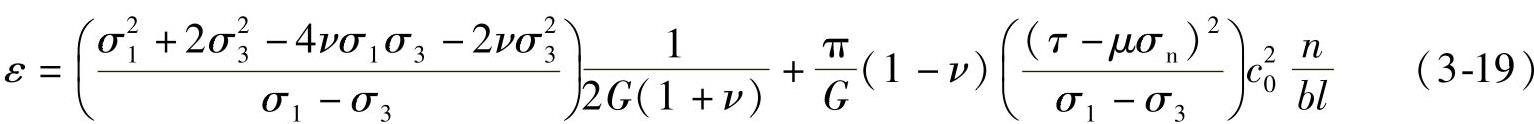
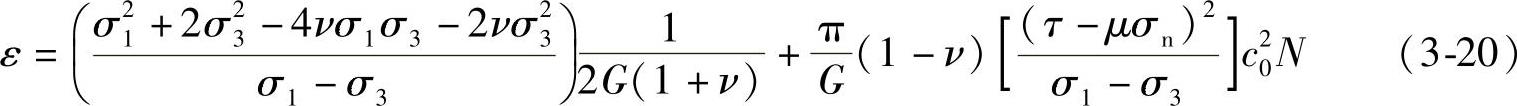
等式中的ε是可以通过室内试验测得的一个临界值，通过应力-应变曲线获得。裂纹扩展的临界长度可以由Griffith提出的裂纹扩展的应变能释放率的关系来获得，即dW/dc₀=2Ω。

因此就有

得出裂纹扩展的临界长度为

根据式（3-20）和式（3-22）可以得到N为

式中 。

通过上一章的卸载试验获得了相应的应力-应变关系曲线图（见图3-5），卸载曲线1为非稳定扩展阶段进行卸载。卸载曲线2为从非稳定扩展阶段开始点卸载。根据图3-3的定义，通过计算，获得两次卸载的耗散能量值分别为W_s1=62.5J和W_s2=25J。根据应力分段，选取非稳定扩展点卸载曲线作为裂纹扩展临界能量值。可以估算一下，此刻试件中的未产生贯通的裂纹条数。其中单条裂纹的扩展能量可以根据式（3-17）求得W_s0≈0.02J。根据式（3-23），那么试件中的裂纹条数应该为1250条左右。通过上面的数据可以认为，对于较为完整的脆性岩石，裂纹扩展的初级阶段应该是与试件的颗粒粒径相关。

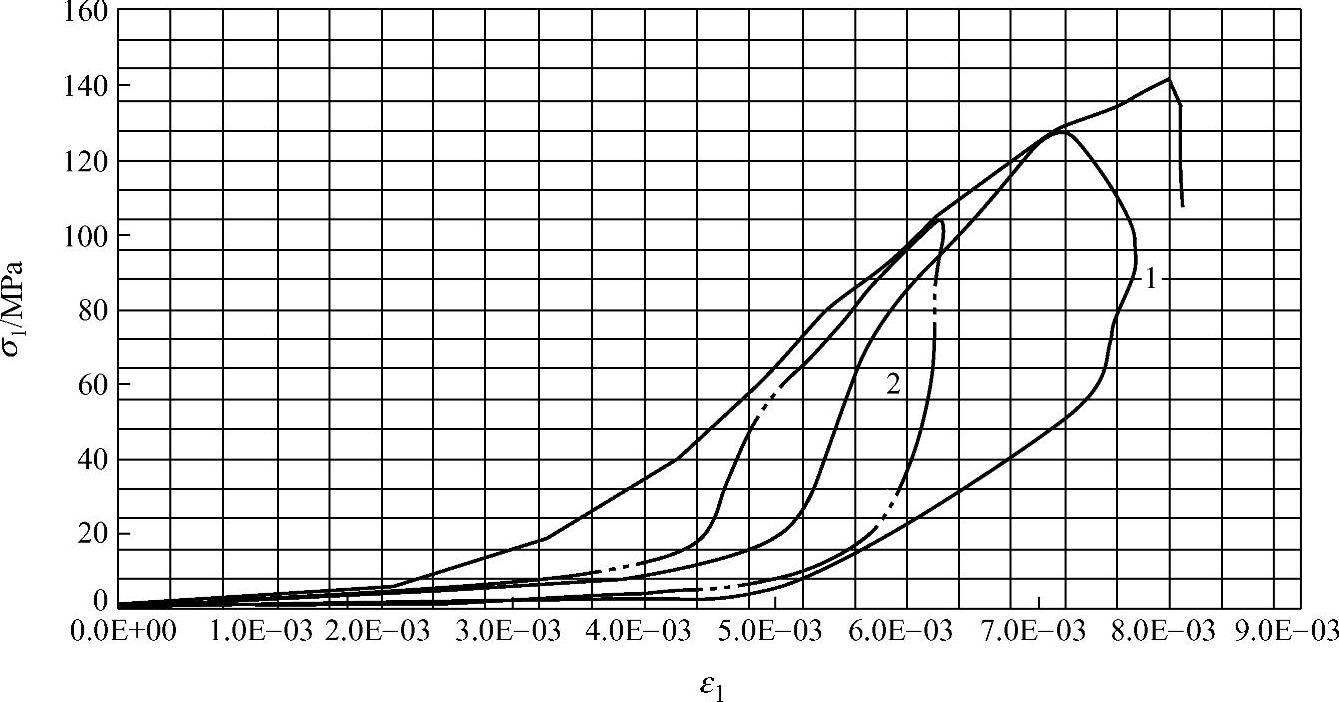
图3-5 单轴压缩情况下卸载试验应力-应变曲线