裂纹扩展中的应变能释放率和能量守恒定律

1.应变能释放率

Griffith^[146]利用能量方法提出了裂纹张开的准则。对于含有一条裂纹的岩石试件初始弹性模量为E_c0。当裂纹扩展到c₀+dc₀时候，弹性模量变为E_c0+dc0。

如果系统进行了边界约束，则应变是常数，荷载随着裂纹扩展必然降低。若有初始长度为c₀的裂纹，试件内总能量为OAC，当裂纹扩展为c₀+dc₀时，试件内总能量为OBC。因此，此过程中的能量变化为OAB（见图3-2）。这个能量值应该大于等于裂纹的表面能才能使得裂纹产生扩展。

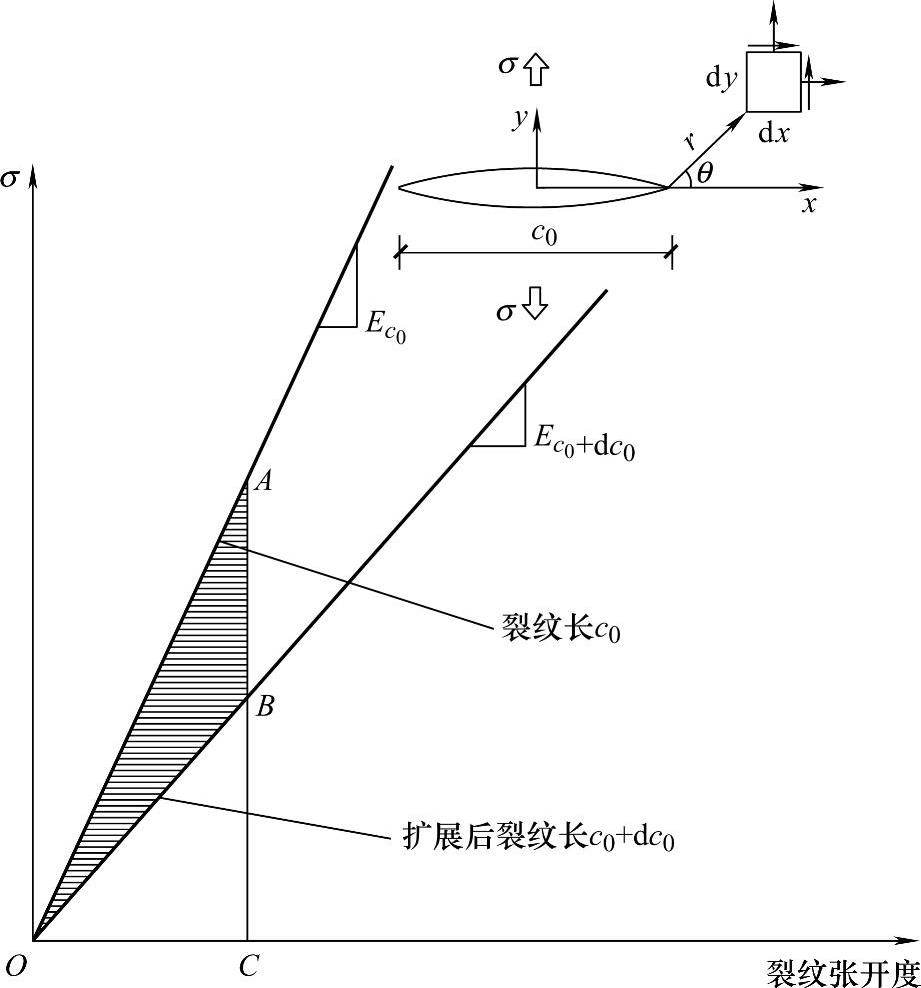
图3-2 单轴拉伸状态下Griffith裂纹扩展条件

基于这个观点，提出裂纹开裂的临界值为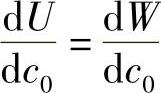，其中U为试件中的弹性应变能，W为裂纹扩展需要的能量。

Griffith认为裂纹扩展的临界条件为

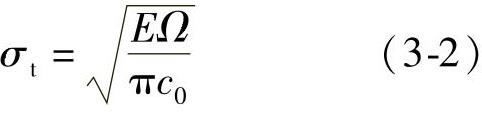
式中 Ω——每个裂纹尖端的应变能释放率，对于平面应变条件下，即

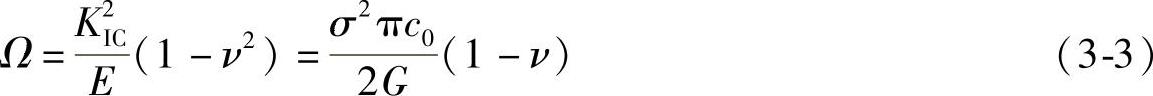
式中 K_IC——岩石的断裂韧度。

应变能释放率Ω与单位厚度裂纹表面断裂比能γ₀的关系是Ω=2γ₀。因此可以推求出(www.xing528.com)

2.能量守恒定律

考虑一个岩石试件在外荷载作用下产生变形，假设该物理过程与外界没有热交换，即封闭系统，外力功所产生的总输入能量SD，根据热力学第一定律，可以得到

WD=SE+W_s （3-5）

式中 SE——试件中的弹性应变能；

W_s——试件中的耗散能，用于形成试件内部的损伤和塑性变形，其变化原则应该满足热力学二定律，即内部状态改变符合熵增加的趋势。

如图3-3所示，W_s代表耗散能，阴影部分面积SE代表试件中可以释放的弹性应变能。从热力学观点分析，能量耗散W_s是单向，不可逆的。能量释放则是双向的，在一定条件下是可以恢复的、是可逆的。

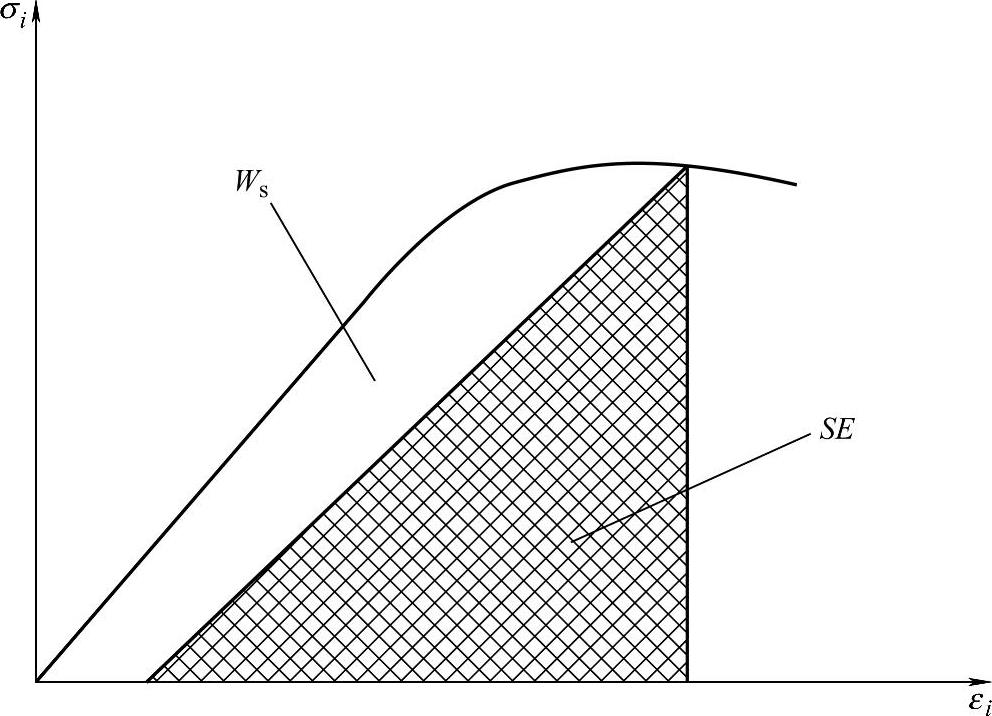
图3-3 岩石破坏过程中的能量分布示意图

由热力学定律可知，耗散能量是岩石变形破坏的本质属性。它反映了岩石内部微小缺陷不断发展，直到形成裂纹甚至节理裂隙的过程。在此过程中，岩石的强度不断的弱化并最终丧失承载能力。因此能量耗散应该与损伤和强度丧失直接相关。耗散量反映了原始强度的衰减程度，一般表现为试件中黏聚力的损失和摩擦力的增大。下文将详细分析这个变化过程。本书主要研究裂纹扩展对试件的影响，因此假定此能量全部用于裂纹的扩展而耗散[147]。