脆性岩石破坏的多阶段特征分析

通过实验室对10组二滩工程正长岩试件试验所获得数据的平均值得到的全应力应变曲线，共分为5个阶段（见图3-1）：

图3-1 二滩工程正长岩试件全应力-应变曲线

1.压密阶段（OA）

此阶段是试件中的微小裂纹产生闭合，是试件压密的过程。虽然压缩变形具有非线性特征。但是在该区域进行加载和卸载试验，岩石的结构和性质并不发生可逆的变化，此阶段属于一种平衡态。

2.弹性阶段（AB）

此阶段是试件的裂纹被压密后，岩石试件的表现为线性、各向同性、弹性变形特性。它的确定可以通过图中裂纹引起的体积应变曲线获得，弹性段时，其应变值保持零状态。此阶段系统内部没有宏观不可逆过程，处于均匀的变形状态，因此同样是一种平衡态。

3.裂纹稳定破裂发展阶段（BC）

1921年Griffith^[62]指出脆性材料的张性破裂是由于微裂纹的存在引起的。并提出岩石的抗拉强度为

式中 E——岩石的变形模量；

γ₀——材料的单位厚度表面断裂比能；(www.xing528.com)

c₀——岩石中所含裂隙长度。

而且还进一步得到单轴抗压强度和抗拉强度的关系是σ_f=8σ_t。以二滩工程为例，其围岩的抗拉强度测得是5MPa左右，根据Griffith的理论则单轴抗压强度值应为40MPa左右，而实际测得的强度值是140MPa。许多学者如Bieniawski^[143]、Brace等^[144]为此也做了许多试验，通过验证，都得到一种普遍的观点，他们认为一旦微裂纹周边的应力水平达到能够克服裂纹断裂表面能的程度，破坏就会发生。

在低围压或者单轴受力状态下，当应力水平在8σ_t时，裂纹就开始扩展，但是这个阶段裂纹的扩展是稳定的并不会发生破裂。

应用Ashby^[2]对椭圆形裂纹应力分析可以验证为什么此阶段裂纹是稳定的。假定一条倾斜椭圆裂纹在岩石试件中受到压缩应力作用。当应力值较小时候，在裂纹尖端产生张拉应力。当超过抗拉强度时，裂纹将开始扩展并沿着压缩应力方向进行扩展。然而在远离裂纹一定距离之后张应力消失，因此裂纹扩展直到荷载值继续增长才得以进行。

通过试验得到对于二滩工程的围岩，当荷载达到峰值强度的0.3倍时，就达到了裂纹的稳定扩展点σ_ci。这个阶段最大的特点是裂纹将开始沿着加载方向扩展，为劈裂裂纹的形成提供了最基本解释。

通常情况下σ_ci很难通过应力-应变曲线得到，但本书通过体积应变跟轴向应变的关系来确定。其中图3-1中的裂纹引起的体积应变可以通过下面方法获得。

确定弹性体积应变为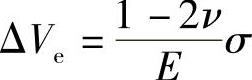，则裂纹引起的体积应变就是总的测得的体积应变与弹性体积应变的差值。σ_ci就是裂纹引起体积应变开始增长即剪胀开始的位置，即对应图3-1的B点。当强度值高于σ_ci不大时，虽然会产生裂纹的扩展，但不会降低岩石试件的整体强度。总之，此阶段变形出现不可逆过程，但这种过程容易被控制。如果在此阶段停止加载，经过一定时间后系统将可能得到一个宏观上不随时间变化的恒定状态，即是定态。此阶段的裂纹产生类型与不稳定裂纹增长阶段不同，裂纹类型一般很难观测到，这是因为脆性岩石包含许多微小裂隙。这些裂隙中又包括颗粒边界、边界之间的空洞、刚度差异较大的颗粒组合、颗粒之间的劈裂面等。

4.裂纹的非稳定扩展阶段（CD）

从轴向应力-应变关系曲线中，可以认为当总体积应变开始发生突变的时候，表示裂纹的非稳定阶段的开始。起始点一般从峰值强度的0.6～0.7倍左右发生。此时轴向应力-应变曲线表现出明显的非线性关系，裂纹必定沿着颗粒边界产生滑移，产生宏观的破裂面。但从图3-1可以看出当应力水平超过0.7倍峰值强度时，破坏很容易瞬时发生。此时如果将荷载值保持不变，材料也将不能承载。Hallbauer等^[145]指出这个阶段会引起试件结构发生明显的变化，而且裂纹密度将会出现成倍的增长。这种现象可以通过声发射定位来获得。总之，进入该阶段后，微破裂的发展发生质的变化，由于破裂过程中所造成的应力集中效应显著。即使施加的应力水平保持不变，破裂仍会不断地累积性发展，使薄弱环节依次破坏。此时体积应变转为膨胀，轴向应变率和侧向应变率加速增大。微裂纹在空间的分布出现应变局部化，即从无序向有序转化。此时系统一方面从外界吸收能量，另一方面又因微裂纹发展释放能量。系统的宏观状态也将随时间变化如变形速率增大，膨胀。这是一种远离平衡的非平衡态。

5.峰后阶段（D点以后）

岩体内部的微破裂面发展为贯通性的结构面。加载荷载大于岩石试件的承载能力，使得变形急剧增大，对脆性岩石甚至出现岩爆等剧烈的破坏现象。